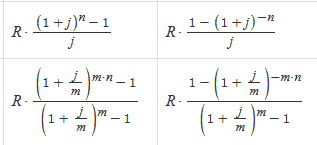Метод золотого сечения
Этот алгоритм используется для нахождения минимума функции. Если необходимо найти нули функции, то используется другой алгоритм.Правила ввода функции
1)
10•x•e2x ≡ 10*x*exp(2*x)
2)
x•e-x+cos(3x) ≡ x*exp(-x)+cos(3*x)
3)
x3-x2+3 ≡ x^3-x^2+3
Не всегда можно определить заранее, сколько раз придется вычислять функцию. Метод золотого сечения почти столь же эффективен при n-2, что и метод Фибоначчи, однако при этом не требуется знать n – количество вычислений функции.
Сущность этого метода заключается в следующем. Интервал неопределенности делится на две неравные части так, что отношение длины большего отрезка к длине всего интервала равно отношению длины меньшего отрезка к длине большего (рис 3).
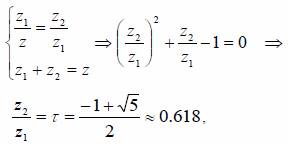
где τ - «золотое сечение»
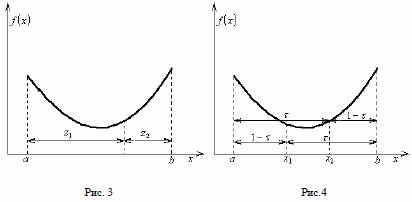
Если длина конечного интервала неопределенности равна δ, то для достижения требуемой точности число вычислений значений функции по методу золотого сечения можно найти по условию

Пример. Методом золотого сечения найти точку минимума x* функции f(x) на отрезке [a;b] с точностью ε и значение целевой функции в этой точке:
f(x)=x4+2x2+4x+1=0, [-1;0], ε=0.1
Решение. Положим a1 = a, b1 = b. Вычислим λ1 = a1 + (1- 0.618)(b1 - a1), μ1 = a1 + 0.618(b1 - a1).
Вычислим f(λ1) = -0.5623, f(μ2) = -0.2149
Итерация №1.
Поскольку f(λ1) < f(μ1), то b2 = -0.382, a2 = a1, μ2 = -0.618
μ2 = a2 + 0.618(b2 - a2) = -1 + 0.618(-0.382 +1), f(μ2) = f(-0.618) = -0.2149
Итерация №2.
Поскольку f(λ2) > f(μ2), то a3 = -0.7639, b3 = b2, λ3 = -0.618
μ3 = a3 + 0.618(b3 - a3) = -0.7639 + 0.618(-0.382 +0.7639), f(μ3) = f(-0.5279) = -0.5623
Итерация №3.
Поскольку f(λ3) < f(μ3), то b4 = -0.5279, a4 = a3, μ4 = -0.618
μ4 = a4 + 0.618(b4 - a4) = -0.7639 + 0.618(-0.5279 +0.7639), f(μ4) = f(-0.618) = -0.4766
Итерация №4.
Поскольку f(λ4) < f(μ4), то b5 = -0.618, a5 = a4, μ5 = -0.6738
μ5 = a5 + 0.618(b5 - a5) = -0.7639 + 0.618(-0.618 +0.7639), f(μ5) = f(-0.6738) = -0.5623
Остальные расчеты сведем в таблицу.
| N | an | bn | bn-an | λn | μn | F(λn) | F(μn) |
| 1 | -1 | 0 | 1 | -0.618 | -0.382 | -0.5623 | -0.2149 |
| 2 | -1 | -0.382 | 0.618 | -0.7639 | -0.618 | -0.548 | -0.5623 |
| 3 | -0.7639 | -0.382 | 0.3819 | -0.618 | -0.5279 | -0.5623 | -0.4766 |
| 4 | -0.7639 | -0.5279 | 0.236 | -0.6738 | -0.618 | -0.5811 | -0.5623 |
| 5 | -0.7639 | -0.618 | 0.1459 | -0.7082 | -0.6738 | -0.5782 | -0.5811 |
| 6 | -0.7082 | -0.618 | 0.09018 | -0.6738 | -0.6524 | -0.5811 | -0.5772 |
Ответ: x = -0.66309052; F(x) = -0.57965758