Численное интегрирование функций

Квадратурные формулы

Если функция f(x) непрерывна на [a,b] и известна ее первообразная F(x), то определенный интеграл от этой функции может быть вычислен по формуле Ньютона-Лейбница

, (1)
где F′(x)=f(x).
Однако во многих случаях F(x) не может быть найдена с помощью элементарных функций или является слишком сложной; поэтому вычисление интеграла (1) может быть практически невыполнимым. Кроме того, на практике подынтегральная функция f(x) часто задается таблично и тогда понятие первообразной теряет смысл. Поэтому важное значение имеют численные методы вычисления определенных интегралов.
Суть численного интегрирования заключается в вычислении значения (1) на основании ряда значений f(x_i), i=0,...,n.
Численное вычисление однократного интеграла (интеграла от функции одной переменной) называется квадратурой, а двойного – кубатурой. Соответствующие формулы мы будем называть квадратурными и кубатурными.

Рассмотрим вычисление однократных интегралов. Обычный прием квадратуры состоит в том, что f(x) на [a,b] заменяют аппроксимирующей или интерполирующей функцией φ(x) простого вида (например, полиномом), а затем приближенно полагают
. (2)
Функция φ(x) должна быть такова, чтобы вычислялся непосредственно.
Если f(x) задана аналитически, то можно ставить вопрос об оценке погрешности формулы (2).
Предположим, что для функции f(x) заданной своими значениями y_i=f(x_i) на сетке {x_i}, i=0,...,n построен полином Лагранжа.
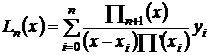, (3)
причем L_n(x_i)=y_i, где П_n+1(x)=(x-x₀)(x-x₁)...(x-x_n).

Заменяя f(x) полиномом L_n(x) получим равенство
, (4)
где R_n - ошибка квадратурной формулы (4) (остаточный член).
Подставим (3) в (4) получим приближенную квадратурную формулу
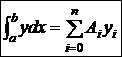, (5)
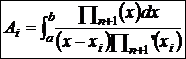где . (6)
Коэффициенты A_i не зависят от функции f(x), а зависят лишь от расположения узлов сетки x_i.
Следует заметить, что если f(x) является полиномом степени n, то формула (5) – точная, т.к. в этом случае f(x)≡L_n(x); следовательно, формула (5) является точной, например, еслиy=x^k (k=0,...,n), т.е. R_n|x^k|=0. В этом случае нет необходимости строить полином Лагранжа, т.к. коэффициенты A_i могут быть найдены из системы уравнений
,
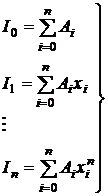где .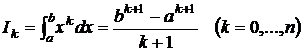

Пример. Вывести квадратурную формулу вида
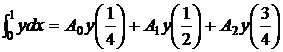. (7)
Решение. Полагая в (7) y=x^k (k=0,1,2) и учитывая, что

получим систему
.
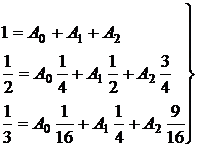Отсюда: A₀=2/3; A₁=-1/3; A₂=2/3.
и, следовательно 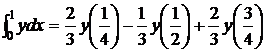(8)
Формула (8) является точной для всех полиномов степени не выше второй.

Квадратурные формулы Ньютона-Котеса

Пусть для данной функции y=f(x) требуется вычислить интеграл

.
Зададим шаг

и разобьем [a,b] на n отрезков с помощью равноотстоящих точек
i=a+i·h, i=0,...,n.
Пусть y_i=f(x_i).
Заменяя функцию f(x) интерполяционным полиномом Лагранжа L_n(x), получим квадратурную формулу

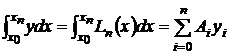. (1)
Получим явные выражения для коэффициентов A_i формулы (1).
С помощью подстановки

полином Лагранжа примет вид

.
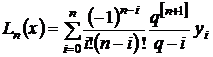Подставим L_n(x) в (1) и приравняем сомножители при y_i. В результате получим для A_i

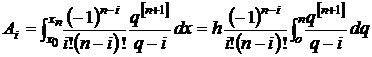, (2)

Подставим в (2)

и введем величины H_i (коэффициенты Котеса)

,
где

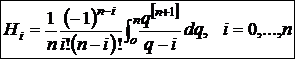. (3)

Тогда (1) примет вид
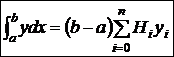, y_i=f(x₀+i·h). (4)
Справедливы соотношения:
1)
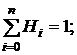
2) H_i=H_n-i.
Первое свойство 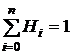получается следующим образом. Если в формуле (4) положить y≡1, то получим
.
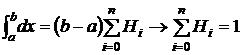Второе свойство доказывается непосредственными вычислениями.

Формула трапеции

Формула Симпсона

Формула прямоугольников

Квадратурная формула Чебышева

Рассмотрим квадратурную формулу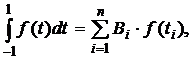

(1)
где B_i - коэффициенты. Зададим коэффициенты B_i равны между собой. Абсциссы t_i будем выбирать таким образом, чтобы квадратурная формула (1) являлась точной для всех полиномов до степени n включительно.
Найдём B_i и t_i. Полагая B₁=B₂= ... = _n=B и учитывая, что при f(t)≡1 будем иметь

,
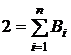получаем

.
Следовательно, квадратурная формула (1) примет вид

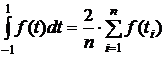. (2)
Найдём теперь t_i. Формула (2), согласно второму условию, должна быть точной для функций вида
f(t)=t,t²,...,tⁿ.
Подставляя эти функции в (2), получим систему уравнений

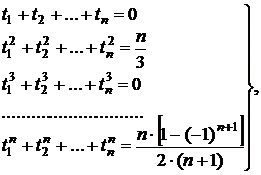(3)
из которой могут быть определены неизвестные t_i, i=1,2,..,n. Формула (2), в которой абсциссы определяются системой (3), называется квадратурой Чебышева.
Система (3) при n=8 и n≥10 не имеет действительных решений. В этом состоит принципиальный недостаток формулы Чебышева.
Получим значения t_i для n=2 и n=3.
1) n=2. Система (3) примет вид

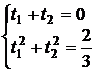
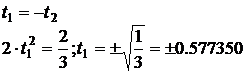
В результате получаем t₁=-0.577350; t₂=0.577350.
2) n=3.

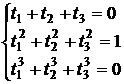(4)
Из решения системы (4) получим:

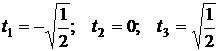. Таким образом, формула Чебышева имеет вид

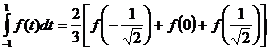Чтобы применить формулу Чебышева к интегралу вида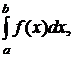
следует преобразовать его с помощью подстановки
,
переводящей отрезок a≤x≤b в отрезок -1≤t≤1. В результате получим
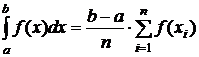, (5)

где t_i - корни системы (4).
В заключение приведём значения t_i для n=2,3,..,8:

n	i	t_i	n	i	t_i
2	1;2	±0.577350	6	1;6	±0.866247
3	1;3	±0.707107		2;5	±422519
	2	0		3;4	±0.266635
4	1;4	±794654	7	1;7	±0.883862
	2;3	±0.187592		2;6	0.529657
5	1;5	±0.832498		3;5	±0.323912
	2;4	±374541		4	0
	3	0

Квадратурная формула Гаусса

Здесь нам потребуются некоторые сведения о полиномах Лежандра. Полиномы вида

называются полиномами Лежандра. Свойства полиномов Лежандра:
1) P_n(1)=1, P_n(-1)=(-1)ⁿ (n=0,1,2...)
2) Свойство ортогональности:

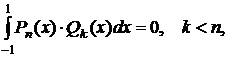
где Q_k(x) - любой полином степени k<n.

Пример
Q₁=1+x
P₂(x)·Q₁(x)=P₂(x)+x·P₂(x)

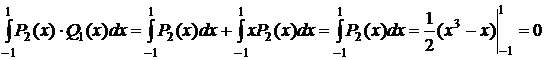
Второе слагаемое здесь равно нулю, т.к. подынтегральная функция нечетная.
3) Полином Лежандра имеет n различных и действительных корней, которые расположены на интервале (-1, 1).
Перейдём теперь к выводу квадратурной формулы Гаусса. Рассмотрим функцию y=f(x) на [-1, 1]. Поставим задачу: как нужно подобрать точки t₁, t₂,..., t_n и коэффициенты A₁, A₂,..., A_n, чтобы квадратурная формула

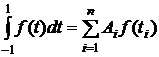(8.4.1)
была точной для всех полиномов f(t) наивысшей возможной степени N=2n-1 (т. к. нужно определить 2n коэффициентов {A_i, t_i}, а полином степени 2n-1 имеет 2n коэффициентов).
Для обеспечения равенства (8.4.1) необходимо и достаточно, чтобы оно было верным при

.
При этом мы получим следующую систему уравнений относительно A_i, t_i:
f(t)=1, t, t², ..., t^2n-1. (8.4.2)

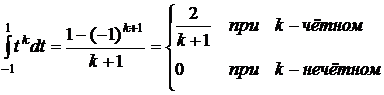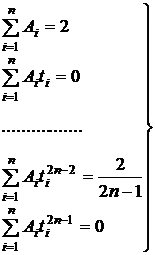Таким образом, учитывая соотношение

получим из (8.4.2) систему из 2n уравнений для определения коэффициентов A_i и узлов t_i:

(8.4.3)
Система (8.4.3) нелинейная и её решение обычным путём вызывает большие математические трудности. Применим следующий искусственный приём: рассмотрим полиномы
f(t)=t^kP_n(t), k=0,1,..,n-1
где P_n - полином Лежандра. На основании (8.5.1) мы можем записать

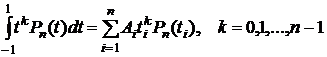. (8.4.4)
С другой стороны, в силу свойства ортогональности полиномов Лежандра (свойство 2), имеем

,
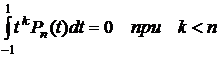поэтому (8.4.4) дает следующие равенства

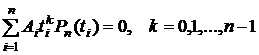. (8.4.5)
Равенства (8.4.5) будут заведомо выполнены при любых A_i, если положить
P_n(t_i)=0, i=1,2,..,n. (8.4.6)
Т.о., если в качестве t_i взять нули полинома P_n(t), то мы обеспечиваем наивысшую точность квадратурной формулы (8.4.1) для всех полиномов степени N=2n-1. Как известно (свойство 3), эти нули действительны, различны и расположены на (-1, 1). Зная t_i, легко находим из линейной системы первых n уравнений (8.4.3) коэффициенты A_i (i=1,2,..,n). Определитель этой системы есть определитель Вандермонда

и, следовательно, A_i определяются однозначно. Формула (4), где t_i - нули полиномов Лежандра P_n(t) и A_i определяются из системы (8.4.3), называется квадратурной формулой Гаусса.
Получим квадратурную формулу Гаусса для n=3 (три точки). Полином Лежандра 3-ей степени есть

.
Приравнивая P₃(t)=0, находим

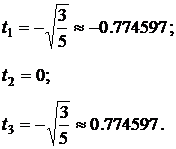
Для определения A_i имеем систему

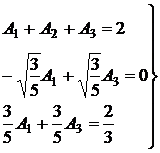
Отсюда A₁=A₃=5/9; A₂=8/9. Следовательно,

.
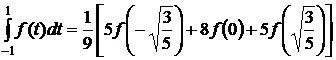Для произвольного интервала [a;b] формула Гаусса имеет вид

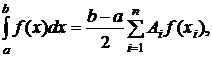(8.4.7)
где

,
t_i - нули полинома Лежандра P_n(t). Остаточный член формулы Гаусса (8.4.7) с n узлами определяется следующим образом:

.
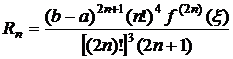В частности,

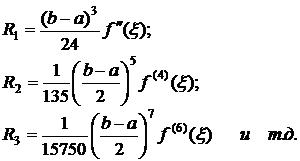
В таблице приведены значения t_i, A_i для n=1,2,..,8:

n	i	t_i	A_i
1	1	0	2
2	1;2	±0.57735027	1
3	1;3	±0.77459667	0.55555556
	2	0	0.88888889
4	1;4	±0.86113631	0.34785484
	2;3	±0.33998104	0.65214516
5	1;5	±0.90617985	0.23692688
	2;4	±0.53846931	0.47862868
	3	0	0.56888889
6	1;6	±0.93246951	0.17132450
	2;5	±0.66120939	0.36076158
	3;4	±0.23861919	0.46791394
7	1;7	±0.94910791	0.12948496
	2;6	±0.74153119	0.27970540
	3;5	±0.40584515	0.38183006
	4	0	0.41795918
8	1;8	±0.96028986	0.10122854
	2;7	±0.79666648	0.22238104
	3;6	±0.52553242	0.31370664
	4;5	±0.183434464	0.36268378

О точности квадратурных формул

Рассмотренные нами квадратурные формулы имеют следующую структуру: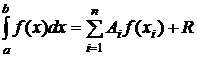

,
где x₁, x₂,..., x_n - система узлов на [a,b], A_i - некоторые известные постоянные коэффициенты, R - остаточный член. При одном и том же числе ординат точность различных квадратурных формул различна.

Пример. Сравнить точность различных квадратурных формул при n=3 для интеграла
.

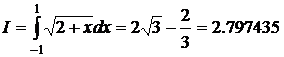Решение: Формула Симпсона дает

Формула Чебышева

Формула Гаусса

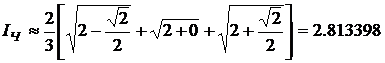
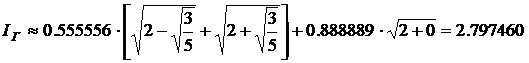
Таким образом, здесь формула Гаусса является наиболее точной.
Точность квадратурной формулы для фиксированного числа узлов существенно зависит от расположения этих узлов. При неудачном выборе узлов квадратурная формула может дать сильно искажённые результаты. Например, для функции y=f(x) (см. ниже) выбирая равноотстоящие узлы a=x₀, x₁, x₂, x₃, x₄=b и пользуясь формулой Ньютона - Котеса (или любой другой) для пяти ординат, получим

,
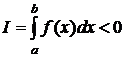тогда как очевидно, что I>0:

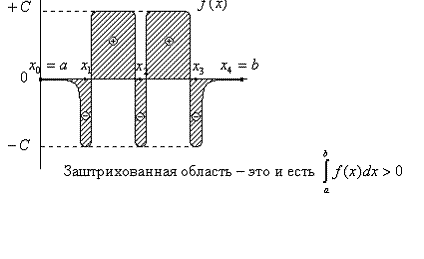
Вообще, при наличии значительного числа нулей подынтегральной функции f(x) или при большом числе экстремумов (т. е. когда имеется большое количество нулей f′(x)), точность квадратурных формул сильно снижается. Поэтому шаг h нужно выбирать так, чтобы он был намного меньше расстояний между соседними нулями функции f(x) и её производной f′(x).
Практические рекомендации:
1) Если подынтегральная функция f(x) задана таблично, то для численного интегрирования мы не можем использовать формулы Гаусса, Чебышева. Поэтому в этом случае применяют формулы трапеций, Симпсона (основанные на интерполяционном полиноме Лагранжа), прямоугольников (лево- и правостороннюю). Другой способ – это предварительно построить другой интерполяционный полином и затем вычислить интеграл. Одним из наиболее широко применяемых полиномов является кубический интерполяционный сплайн. Вычислив коэффициенты сплайна a_i, b_i, c_i, d_i, рассчитываем затем интеграл по формуле

,
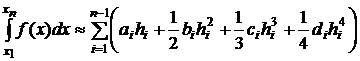где h_i=x_i+1-x_i.
2) Если функция f(x) задана аналитически, то полезно предварительно построить график этой функции. В случае если она окажется сильно осциллирующей, то следует применять специальные приёмы численного интегрирования. Один из них заключается в выделении подинтервалов, в которых содержится один нуль функции f(x) или f′(x). Разбив весь интервал на эти подинтервалы, мы затем вычисляем численно интеграл в каждом таком подинтервале по одной из квадратурных формул, и потом складываем эти интегралы.
Для вычисления интегралов на подинтервалах мы можем использовать любую квадратурную формулу. Наибольшей точностью обладает квадратурная формула Гаусса. Для достижения заданной точности поступают следующим образом. Пусть задана точность ε, число подинтервалов оказалось равным m. Тогда, если погрешность вычисления

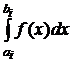меньше

, то погрешность

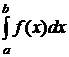будет меньше ε.
3) Для достижения заданной точности вычисления интеграла от f(x), заданного аналитически, можно использовать следующий способ. Пусть I_k - значение интеграла при числе узлов n=k, I_k+1 - n=k+1. Используя квадратурную формулу Гаусса, увеличение числа узлов проводят до тех пор, пока |I_k-I_k+1<ε|, где ε - заданная точность. Если используют формулу Симпсона, то число узлов на каждой итерации обычно удваивают (шаг уменьшают в два раза).

Наименование квадратурной формулы	Остаточный член соответствующей квадратурной формулы
Формула левых прямоугольников и правых прямоугольников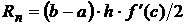
Формула средних прямоугольников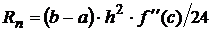
Формула трапеции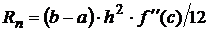
Формула Симпсона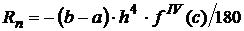

Вычисление несобственных интегралов

Интеграл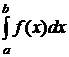

(8.7.1)
называется собственным, если:
1) промежуток интегрирования [a,b] конечен;
2) подынтегральная функция f(x) непрерывна на [a,b].
В противном случае интеграл (8.7.1) называется несобственным. Рассмотрим сначала вычисление интеграла

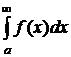(8.7.2)
с бесконечным промежутком интегрирования, где f(x) - непрерывна при a≤x≤∞.
Интеграл (8.7.2) называется сходящимся, если существует конечный предел

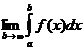. (8.7.3)
В этом случае полагают

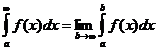. (8.7.4)
Если предел (8.7.3) не существует, то интеграл (8.7.2) называется расходящимся и лишён смысла. Поэтому, прежде чем приступить к вычислению несобственного интеграла, нужно предварительно убедиться, что этот интеграл сходится.
Чтобы вычислить сходящийся несобственный интеграл (8.7.2) с заданной точностью ε, представим его в виде

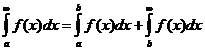, (8.7.5)
где b выбирают столь большим, чтобы имело место неравенство

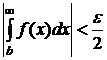. (8.7.6)
Собственный интеграл

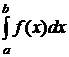вычисляется по одной из квадратурных формул с точностью до

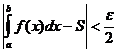, (8.7.7)
где S - приближённое значение интеграла

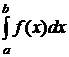. Тогда

,
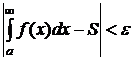и поставленная задача будет решена.
Перейдём теперь к вычислению интеграла (8.7.1), где f(x) имеет конечное число точек разрыва на интервале [a,b]. Промежуток интегрирования разбиваем на частичные промежутки с единственной точкой разрыва. Итак, пусть f(x) имеет одну точку разрыва. Пусть эта точка x=c.

Точка разрыва называется точкой разрыва 1-го рода, если существуют конечные односторонние пределы слева и справа, т.е.
; .
Точка разрыва c называется точкой разрыва 2-го рода, если один из односторонних пределов не существует, или в точке c функция f(x) не определена.

Пример. Функции имеют в точке x=0 разрыв 2-го рода. Функция в точке x=0 имеет правосторонний предел b₂=0 и левосторонний предел b₁=1:

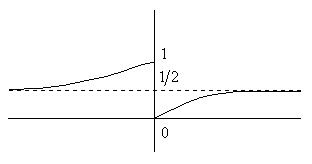
Если в точке x=c разрыв 1-го рода, то можно положить
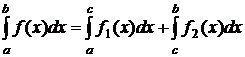, (8.7.8)
где .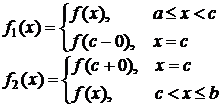
Интегралы 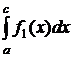и 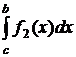вычисляем по квадратурной формуле с точностью до <ε/2.
Если в точке x=c f(x) имеет разрыв 2-го рода, то полагают
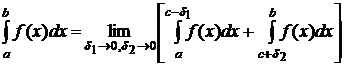, (8.7.9) и в случае существования этого предела интеграл называется сходящимся, в противном случае – расходящимся.
Для приближённого вычисления сходящегося интеграла (8.7.9) с заданной точностью ε выбирают δ₁>0 и δ₂>0 столь малыми, чтобы имело место неравенство
.
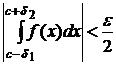Затем по известным квадратурным формулам приближённо вычисляют собственные интегралы
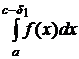и 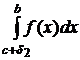. (8.7.10)
Очевидно, что если S₁ и S₂ - приближённые значения интегралов (8.7.10) с точностью до ε/4, то 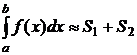с точностью до ε.

Примеры. Решить дифференциальное уравнение y¢=y+2x+1, y(0)=0, xÎ[0,1],h=0.5
1) метод численного интегрирования:
Формулы, по которым подсчитывается значение очередного приближения для трех узлов (x0=0, x1=0.5, x2=1):
y⁽ⁿ⁾ (x1)-y(x0)=h/12[5f(x0,y^(n-1) (x0))+8f(x1,y^(n-1) (x1))-f(x2,y^(n-1) (x2))];
y⁽ⁿ⁾ (x1)-y(x0)=h/3[5f(x0,y^(n-1) (x0))+4f(x1,y^(n-1) (x1))+f(x2,y^(n-1) (x2))];
По условию, y⁽⁰⁾ (x0)=y(0)=0, x={0 ,0.5, 1}.

n	y⁽ⁿ⁾(x)
0	y⁽⁰⁾(x1)=1/24[5×0+8×(2×0.5+1)-(2×1+1)]=13/24 y⁽⁰⁾(x2)=1/6[5×0+4×(2×0.5+1)+(2×1+1)]=11/6
1	y⁽¹⁾(x1)=1/24[5×0+8×(13/24+2×0.5+1)-(11/6+2×1+1)]=23/36 y⁽¹⁾(x2)=1/6[5×0+4×(13/24+2×0.5+1)+(11/6+2×1+1)]=90/36
2	y⁽²⁾(x1)=1/24[5×0+8×(23/36+2×1+1)-(90/36+2×1+1)]=281/(36×12)=0.65 y⁽²⁾(x2)=1/6[5×0+4×(23/36+2×1+1)+(90/36+2×1+1)]=93/36=2.58

2) метод Рунге-Кутта:
первого порядка
y_i₊₁ =y_i +k1; k1=h×f(x_i ,y_i ).
Результаты вычислений:

i	x_i	y_i	y_i+1
0	0	y₀=0	y₁=0+0.5(0+2·0+1)=0.5
1	0.5	y₁=0.5	y₂=0.5+0.5(0.5+2·0.5+1)=1.75
2	1	y₂=1.75	y₃=1.75+0.5(1.75+2·1+1)=4.125

второго порядка:
y_i+1 =y_i +1/2[k1+k2]; k1=h×f(x_i ,y_i ); k2= h×f(x_i +h,y_i +k1).
Результаты вычислений:

i	x_i	y_i	k1	k2	y_i+1
0	0	y₀=0	0.5	1.25	y₁=0.875
1	0.5	y₁=0.875	0.5(0.875+1+1)=1.4375	2.65625	y₂=2.921875

Приближенное вычисление определенных интегралов

Для вычисления определенного интеграла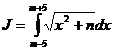

, разбивая отрезок интегрирования сначала на 10 равных частей, а затем на 20 равных частей, найти приближенное значение J₁₀ и J₂₀: а) по формуле трапеций; б) по формуле Симпсона. Оценить точность приближения с помощью разности ε=|J₁₀-J₁₀|.
Тема 2. Численное интегрирование
2.1. Постановка задачи интегрирования
Численное интегрирование функции целесообразно использовать в тех случаях, когда: 1) первообразная F(x) не может быть найдена с помощью элементарных функций; 2)F(x) является слишком сложной; 3) подынтегральная функция f(x) задана таблично или неявно.
Будем рассматривать формулы приближенного вычисления интегралов

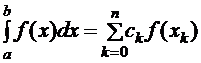, где f(x) –достаточно гладкая функция, xÎ[a,b] и c_k – числа, k=0,1,…,n..
Для составления квадратурных формул данную функцию f(x)заменяют интерполирующей функцией φ(x) и приближенно полагают

≈

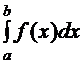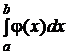
и затем вычисляют интеграл непосредственно, а оценку погрешности формулы определяют исходя из вида функции f(x).

Простейшие формулы Ньютона-Котеса и обобщенные квадратурные формулы

Пусть для функции y=f(x)требуется вычислить интеграл J(f)=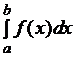

.
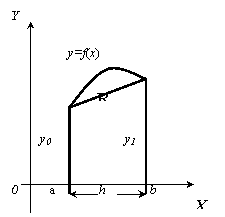
Выбрав шаг h=, разобьем отрезок [a, b] на n равных частей: x₀=a, x_i=x₀+ih(i=1, 2,…, n-1), x_n=bи пусть y_i=f(x_i)(i=0, 1, 2, …, n).

Рисунок 2.1

2.2.1. Формула трапеций.
Пусть n=1.
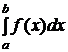=(y₀+y₁)+.
Оценка остаточного члена формулы трапеции:
, .
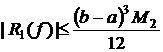Обобщенная формула трапеции для вычисления определенного интеграла на равномерной сетке, запишется так:

где

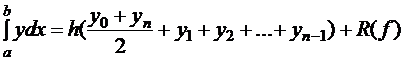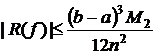2.2.3. Формула парабол (или формула Симпсона)
Формула Симпсона при n=2. Интерполирование функции y=f(x) выполняется по трем ее значениям в точках x₀=a·x₁, , x₂=b, y_i=f(x_i), (i=0,1,2).
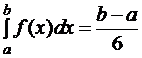(y₀+4y₁+y₂).
Оценка остаточного члена формулы Симпсона:
, .
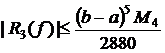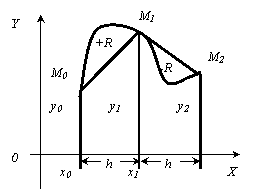
Рис 2.2.

Обобщенная формула Симпсона для вычисления определенного интеграла на равномерной сетке и четного числа шагов, имеет вид:

где

, М₄=

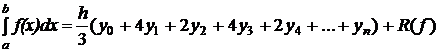, |f^IV(x)|, h=x_i-x_i-1.

2.2.4. Формула «трех восьмых» для вычисления определенного интеграла на равномерной сетке и числа шагов, кратного трем.
При n=3 интерполирование функции выполняется по четырем ее значениям в точках x₀=a, , , x₃=b и y_i=f(x_i), (i=0,1,2,3).
,
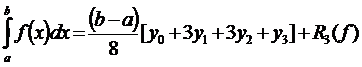где , .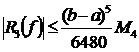
2.2.5. Формула Буля
При n=4.

Оценка остаточного члена формулы:

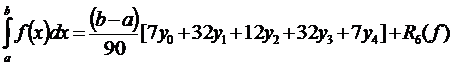
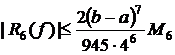Пример. Вычислить приближенное значение интеграла 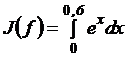, используя обобщенные формулы трапеции, Симпсона, «трех-восьмых», Буля. Оценить остаточный член формул.

Решение.
1) Возьмем количество узлов для трапеции n=6, для Симпсона n=6, для «трех-восьмых» n=6, для Буля n=4.
2) Разобьем отрезок интегрирования [0; 0.6] на n=6 равных частей с шагом h=0.1. Узловые точки найдем по закону x_i=x₀+i*h (i=0,1,2,...,6), x₀=0, x_n=0.6.
3) Вычислим значение подынтегральной функции в полученных узлах y_i=f(x_i), (i=0,1,2,...,6).

i	x_i	y_i
0	0	1,000000
1	0,1	1,105171
2	0,2	1,221403
3	0,3	1,349859
4	0,4	1,491825
5	0,5	1,648721
6	0,6	1,822119

4)Обобщенная формула трапеции:

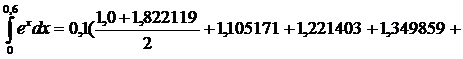1.491825+1.648721) = 0.822804

y″(x)=e^x. Наиб. знач. на отрезке [0; 0.6] при x=0.6, M2=e^0.6=1.822119.

.
5) Обобщенная формула Симпсона:

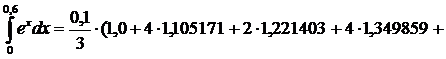2*1.491825+4*1.648721+1.822119) = 0.822119

y^IV(x)=e^x. Наиб. знач. на отрезке [0; 0.6] при x=0.6, M4=e^0.6=1.822119.

.
6) Обобщенная формула «трех восьмых»

=0,822120

y^IV(x)=e^x. Наиб. знач. на отрезке [0; 0.6] при x=0.6, M4=e^0.6=1.822119.

.
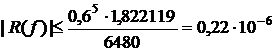7) Формула Буля
h=0.15. Узловые точки x₀=0, x₁=0.15, x₂=0.3, x₃=0.45, x₄=0.6.
y₀=1, y₁=1.161834, y₂=1.349859, y₃=1.568312, y₄=1.822119.

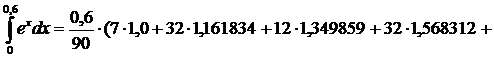7*1.822119) = 0.822119

2. Вычислить приближенное значение интеграла

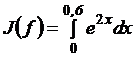, используя
а) формулу трапеции, Симпсона, прямоугольников;
б) обобщенные формулы трапеции, Симпсона, «трех-восьмых», Буля.
Оценить остаточный член формул.
2. Вычислить приближенное значение интеграла

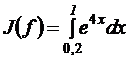, используя
а) формулу трапеции, Симпсона, прямоугольников;
б) обобщенные формулы трапеции, Симпсона, Буля.
Оценить остаточный член формул.
Отделить корни уравнения аналитически или графически и уточнить один из них с точностью до 0,001:
а) методом половинного деления,
6) методом хорд и методом касательных;
в) комбинированным методом;
г) методом итераций
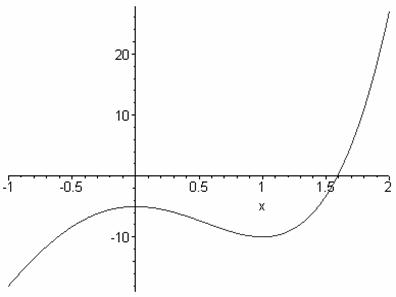
a) 3x⁴ + 4x³ - 12x² -5 = 0
b) x – sinx = 0,25
c) 2x³ -3x² -12x – 5 = 0
d) lnx + (x+1)³ = 0
Отделим корни графическим методом (найдем границы)
a) 3x⁴ + 4x³ - 12x² -5 = 0

Корни лежат в пределах: [1,5; 2]
b) x – sinx = 0,25·

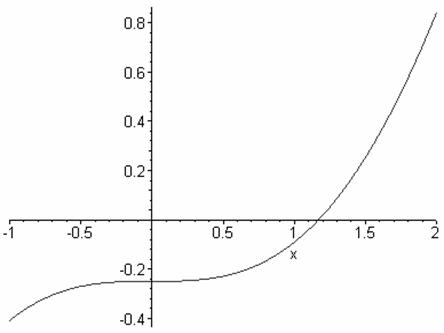
Корни лежат в пределах: [1; 1,5]
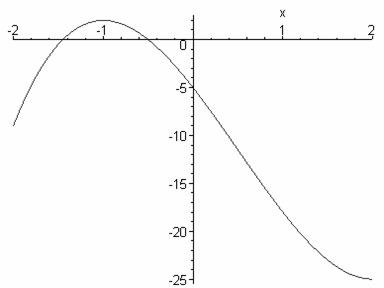
c) 2x³ -3x² -12x – 5 = 0

Корни лежат в пределах: [-2; -1], [-1; 0]
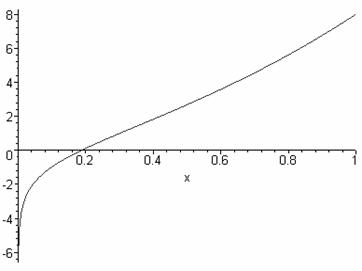
d) lnx + (x+1)³ = 0

Корни лежат в пределах: [0; 0,4]

Решить систему линейных алгебраических уравнений методом простой итерации и методом Зейделя.

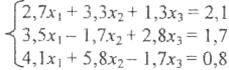
Численное интегрирование

1. Вычислить интеграл по формуле трапеций с тремя десятичными знаками
2. Вычислить интеграл по формуле Симпсона при n = 8 , оценить погрешность результата, составив таблицу конечных разностей
3. Вычислить интеграл по формуле Гаусса

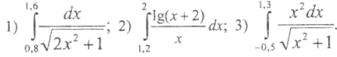
Формула трапеций

Формула Симпсона

Остаточный член формулы Симпсона равен

Формула Гаусса

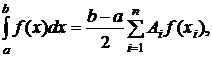
где

t_i - нули полинома Лежандра P_n(t).
1)
Формула трапеций
n = 5

x0	0,8	y0	0,66
x1	1	y1	0,66
x2	1,2	y2	0,58
x3	1,4	y3	0,51
x4	1,6	y4	0,45

I = 0,505
Формула Симпсона
n = 8

x0	0,8	y0	0,662
x1	0,914	y1	0,612
x2	1,029	y2	0,567
x3	1,143	y3	0,526
x4	1,257	y4	0,490
x5	1,371	y5	0,458
x6	1,486	y6	0,430
x7	1,600	y7	0,404

I = 0,397
Остаточный член формулы Симпсона равен R = 0,016
Формула Гаусса
n = 3

n	i	t_i	A_i
3	1;3	±0.77459667	0.55555556
	2	0	0.88888889

b = 1,6; a = 0,8;
∑A_if(x_i) = 1,558
I = 0,623

2)
Формула трапеций
n = 5

x0	1,2	y0	0,42
x1	1,4	y1	0,38
x2	1,6	y2	0,35
x3	1,8	y3	0,32
x4	2	y4	0,30

I = 0,347

Формула Симпсона
n = 8

x0	0,8	y0	0,662
x1	0,914	y1	0,612
x2	1,029	y2	0,567
x3	1,143	y3	0,526
x4	1,257	y4	0,490
x5	1,371	y5	0,458
x6	1,486	y6	0,430
x7	1,600	y7	0,404

I = 0,270
Остаточный член формулы Симпсона равен R = 0,378

Формула Гаусса
n = 3

n	i	t_i	A_i
3	1;3	±0.77459667	0.55555556
	2	0	0.88888889

b = 2; a = 1,2;
∑A_if(x_i) = 1,522
I = 0,60904

3)
Формула трапеций
n = 5

x0	-0,5	y0	0,22
x1	-0,05	y1	0,00
x2	0,4	y2	0,15
x3	0,85	y3	0,55
x4	1,3	y4	1,03

I = 0,863
Формула Симпсона
n = 8

x0	-0,5	y0	0,22
x1	-0,243	y1	0,06
x2	0,014	y2	0,00
x3	0,271	y3	0,07
x4	0,529	y4	0,25
x5	0,786	y5	0,49
x6	1,043	y6	0,75
x7	1,300	y7	1,03

I = 0,489
Остаточный член формулы Симпсона равен R = 0,596

Формула Гаусса
n = 3

n	i	t_i	A_i
3	1;3	±0.77459667	0.55555556
	2	0	0.88888889

b = 1,3; a = -0,5;
∑A_if(x_i) = 0,588582
I = 0,235