Метод сопряженных направлений Пауэлла
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения минимума функции методом Пауэлла. Решение оформляется в формате Word.- Все переменные выражаются через x1,x2
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, x12+x1x2, записываем какx1^2+x1*x2.
Метод Пауэлла относится к прямым методам (методам нулевого порядка). Этим методом наиболее эффективно осуществляется минимизация функций, близких к квадратичным. На каждой итерации алгоритма поиск осуществляется вдоль системы сопряженных направлений.
Два направления поиска Si, Sj называются сопряженными, если SjT·H·Sj=0, i≠j, SiT·H·Si=0, i=j.
где H - положительно определенная квадратная матрица.
Обоснование применения сопряженных направлений в алгоритмах оптимизации. В методе Пауэлла H=▽²f(xk) - матрица вторых частных производных. Идеи метода Пауэлла относятся к квадратичной функции f(x).
Основная идея заключается в том, что если на каждом этапе поиска определяется минимум квадратичной функции f(x) вдоль каждого из p (p < n) - сопряженных направлений и если затем в каждом из направлений делается шаг до минимальной точки, то полное перемещение от начала до шага с номером p сопряжено ко всем поднаправлениям поиска.
Идея использования сопряженных направлений лежит в основе ряда алгоритмов.
Пусть f(x) - квадратичная функция и процесс минимизации начинается в точке x0 с начальным направлением S1. Для удобства возьмем этот вектор единичным, т.е. (S1)T·S1=1. Тогда вектор x1=x0+λ1·S1 и длина шага λ1 определяется из условия минимальности функции в данном направлении т.е.
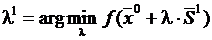 .
.
Для квадратичной функции
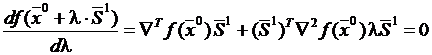 , (1)
, (1)
и, таким образом, оптимальное значение λ на первом шаге определяется в соответствии с соотношением
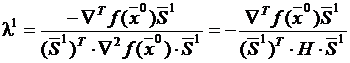 , (2)
, (2)
где H=▽²f(xk).
Из точки x1 процесс минимизации должен осуществляться в другом сопряженном направлении S2 и при этом
(S2)T·H·S1=0.
Квадратичная функция может быть представлена в виде
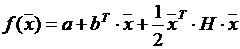 ,
,
где положительно определенная матрица H=▽²f(x).
В общем случае система n линейно независимых направлений поиска S1, S2,..., Sn называется сопряженной по отношению к некоторой положительно определенной матрице H, если (Si)T·H·Sj=0, 0 ≤ i ≠ j ≤ n.
Так как сопряженные направления линейно независимы, то любой вектор в пространстве En можно выразить через S1, S2,..., Sn следующим образом:
где 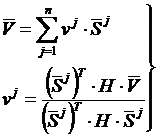 . (3)
. (3)
Для некоторой матрицы H всегда существует, по крайней мере, одна система из n взаимно сопряженных направлений, так как сами собственные векторы матрицы H представляют собой такую систему.
Отметим, что для квадратичной функции справедливо следующее соотношение, которое потребуется в дальнейшем:
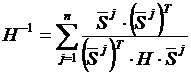 . (4)
. (4)
Чтобы убедиться в его справедливости, рассмотрим матрицу 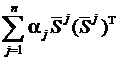 . Умножение ее справа на H·Sk дает
. Умножение ее справа на H·Sk дает
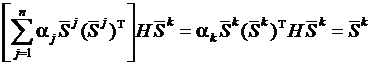 ,
,
если положить 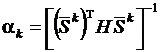 .
.
Вообще говоря, справедливо общее правило, заключающееся в том, что если используются сопряженные направления для поиска минимума квадратичной функции f(x), то эта функция может быть минимизирована за n шагов по одному в каждом из сопряженных направлений. Более того, порядок использования сопряженных направлений несущественен.
Покажем, что это действительно так. Пусть f(x) - квадратичная функция и 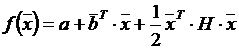 , при этом ▽f(x)=b+H·x.
, при этом ▽f(x)=b+H·x.
В точке минимума ▽f(x*), и эта точка x*=-HT·b.
Заметим, что ▽Tf(xk)·Sk=(Sk)T·▽f(xk).
Так как x1=x0+λ1·S1, (5)
где λ1 определяется в соответствии с соотношением (2):
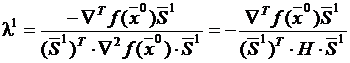 ,
,
затем минимум находится в следующем сопряженном направлении по аналогичным формулам x2=x1+λ2·S2 и т.д., то на n-м шаге имеем
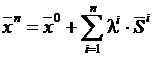 . (6)
. (6)
На каждом шаге минимизируем функцию f(xi-1+λi·Si) в направлении Si, чтобы получить λi, что приводит к следующему выражению (на основании (2))
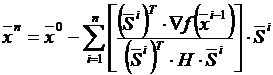 . (7)
. (7)
Кроме того,
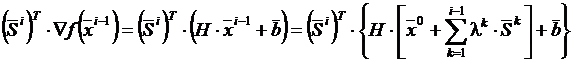 и (Si)T·▽f(xi-1)=(Si)T·[H·x0+b],
и (Si)T·▽f(xi-1)=(Si)T·[H·x0+b],
так как все (Si)T·H·Sk=0, ∀i≠k, Si и Sk – сопряжены.
Таким образом,
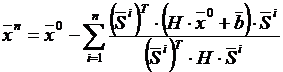 . (8)
. (8)
Выразим векторы x0 и H-1·b через систему сопряженных векторов Si следующим образом (по аналогии с (3)):
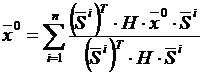 ,
,
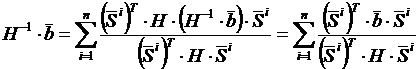 .
.
Подставив эти выражения в (7), получим
xn=x0-x0+H-1·b=H-1·b. (9)
Таким образом, точка xn, полученная в результате минимизации квадратичной функции на n-м шаге, совпадает с точкой минимума квадратичной функции f(x).
Покажем, что для сопряженных направлений, если f(x) каждый раз минимизируется в сопряженном направлении Sj в соответствии с формулой (2), то при этом выполняется следующее равенство:
(xj)T·▽f(xl), 1 ≤ j ≤ l-1,
при использовании не более чем n направлений, то есть ▽f(xl) ортогонален использованным сопряженным направлениям.
Для квадратичной функции ▽f(xl)=b+H·xl. Следовательно,
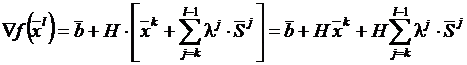 ,
,
где xk - произвольная точка, из которой начинается поиск по сопряженным направлениям. Поскольку ▽f(xk)=b+H·xk,
то 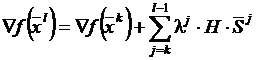 .
.
Умножение этого уравнения слева на (Sk-1)T дает
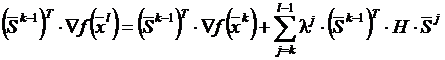 .
.
Первый член в правой части (Sk-1)T·▽f(xk)=0, так как градиент в точке xk ортогонален направлению предыдущего спуска, если точка получена в результате минимизации функции в этом направлении. Кроме того, все остальные слагаемые под знаком суммы исчезают вследствие сопряженности направлений Sk-1 и Sj, и таким образом
(Sj)T·▽f(xl)=0, 1≤j≤l-1. (10)
Алгоритм Пауэлла
Переход из точки xk0 в точку xkn на k-м шаге алгоритма Пауэлла осуществляется в соответствии с формулой: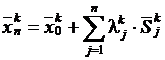 .
.
При этом последовательно осуществляется минимизация исходной функции по сопряженным направлениям Sk1, ... ,Skn. Результатом минимизации по каждому из сопряженных направлений является система параметров λ1k,...,λnk, при которых функция минимальна в каждом из сопряженных направлений:
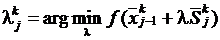 ,
, 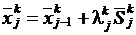 .
.
Начальную систему сопряженных направлений можно выбрать параллельной осям системы координат. В конце каждой итерации алгоритма Пауэлла необходимо выбрать новую систему сопряженных направлений, так как если этого не сделать, то получим простой покоординатный поиск. В основе построения новой системы лежит следующая теорема.
Теорема: Если при начальной точке x0 поиска в направлении вектора S минимум функции f(x) находится к точке xa, а при начальной точке x1≠x0 поиск минимума функции f(x) в том же направлении S приводит к точке xb, то при f(xb)<f(xa) направление xb-xa сопряжено с направлением поиска S.
Доказательство. Используя ранее полученные результаты (10), можно записать, что в первом случае
ST·▽f(xa)=ST·(H·xa+b)=0,
аналогично, во втором случае можно записать
ST·▽f(xb)=ST·(H·xb+b)=0,
Вычитая из первого выражения второе получим, что
ST·H·(xb-xa)=0,
Следовательно, векторы S и (xb-xa) являются сопряженными.
Эта теорема непосредственно может быть распространена на случай нескольких сопряженных направлений следующим образом. Если, начиная из точки x0, точка xa определяется после использования при минимизации нескольких сопряженных направлений p (p<n). И, аналогично, если из точки x1≠x0 точка xb определяется после использования тех же направлений и функция f(x) минимизируется на каждом шаге, то вектор (xb-xa) сопряжен ко всем p направлениям.
Следующий рисунок служит иллюстрацией теоремы.
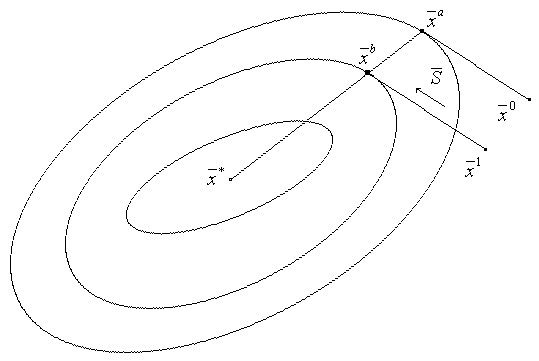
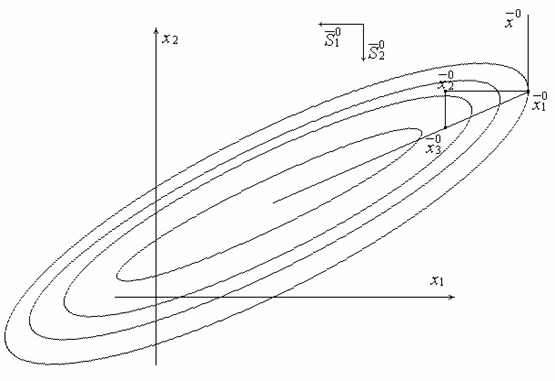
Рисунок.
Пусть в начальный момент для двумерной задачи поиск осуществляется из точки x0 вдоль направлений, параллельных осям координат: S01 и S02. Последовательно были найдены точки x01, x02, x03 (см. рис.).
Таким образом, определили 2 сопряженных направления, в которых следует вести поиск: S02 и (x03-x01). В системе исходных направлений S01 должно быть заменено на (x03-x01), представляющее собой полное перемещение из первого минимума. Направления поиска на следующем этапе:
S11=S02,
S12=x03-x01.
Второй этап начинается с минимизации вдоль направления S12, затем, если необходимо, перемещение в направлении S11. Но в случае квадратичной функции двух переменных после минимизации по двум сопряженным направлениям будет достигнута точка минимума.
В общем случае, на k-м шаге алгоритма Пауэлла используется n линейно независимых направлений поиска. Поиск начинается с точки xk0 и осуществляется по следующему алгоритму:
1. Начиная с точки xk0, решается последовательность задач минимизации функции 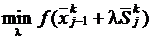 , j=1,n, в направлениях Sk1, ... , Skn. При этом находятся точки xk1, ... , xkn, которые минимизируют исходную функцию в заданных направлениях, причем xk1=xk0+λ1·Sk1 = xk1+λ2·Sk2, ..., xkn=xkn-1+λn·Skn.
, j=1,n, в направлениях Sk1, ... , Skn. При этом находятся точки xk1, ... , xkn, которые минимизируют исходную функцию в заданных направлениях, причем xk1=xk0+λ1·Sk1 = xk1+λ2·Sk2, ..., xkn=xkn-1+λn·Skn.
2. Поиск, осуществляемый на первом этапе, может привести к линейно зависимым направлениям, если, например, в одном из направлений Si не удается найти меньшего значения функции. Поэтому 2 направления могут стать коллинеарными. Поэтому в системе сопряженных направлений не следует заменять старое направление на новое, если после такой замены направления нового набора становятся линейно зависимыми.
На примере квадратичной функции Пауэллом было показано, что при нормировании направлений поиска в соответствии с соотношением:
(Ski)·H·Ski=1, i=1,n,
определитель матрицы, столбцы которой представляют собой направления поиска, принимает максимальное значение тогда и только тогда, когда Ski взаимно сопряжены относительно матрицы H. Он пришел к выводу, что направление полного перемещения на k-м шаге должно заменять предыдущее направление только в том случае, когда заменяющий вектор увеличивает определитель матрицы направлений поиска. Так как только тогда новый набор направлений будет более эффективным.
Для такой проверки из точки xkn делается дополнительный шаг в направлении (xkn-xk0), соответствующий полному перемещению на k-м этапе и получают точку (2xkn-xk0). Для проверки того, что определитель матрицы направлений поиска увеличивается при включении нового направления, делается шаг 3.
3. Обозначим наибольшее уменьшение f(x) на k-м шаге
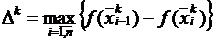 ,
,
соответствующее направление поиска обозначим через Skm.
Обозначим:
f1=f(xk0), f2=f(xkn), f3=f(2xkn-f1=f(xk0),
где xk0=xk-1n, 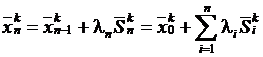 .
.
Тогда, если f3≥f1 и (или) (f1-2f2+f3)(f1-f2-Δk)2≥0.5*Δk(f1-f3)2, то следует использовать на (k+1)-м этапе те же направления Sk1, ... , Skn, что и на k-м этапе, то есть Sk+1i=Ski, i=1,n, и начать поиск из точки xk+10=xkn или из точки xk+10=2xkn-xk0=xkn+1, в зависимости от того, в какой точке функция принимает минимальное значение.
4. Если тест на шаге 3 не прошел, то ищется минимум f(x) в направлении вектора Skn+1, проведенного из xk0 в xkn: Skn+1=(xkn-xk0). Точка этого минимума берется в качестве начальной точки на (k+1)-м этапе. А в системе сопряженных направлений сохраняются все, кроме направления Skm, которое заменяется на новое направление Skn+1, но новое направление помещается в последний столбец матрицы направлений. На (k+1)-м этапе будут использоваться направления
[Sk+11, Sk+12, ..., Sk+1n] = [Sk1, Sk2, ..., Skm-1, Skm+1, ... , Skn, Skn+1].
5. Критерий останова. Алгоритм прерывается, если изменение по каждой переменной оказывается меньше заданной точности по соответствующей переменной или ||xkn-xk0||≤ε.
Пример №1. Методом Пауэлла найти точку минимума функции 4(x1-5)2+(x2-6)2, если задана начальная точка х(0) = (8, 9)Т.
Решение:
Градиент функции: 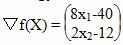
Итерация №0.
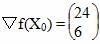
Проверим критерий остановки: |▽f(X0)| < ε
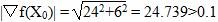
Вычислим значение функции в начальной точке f(X0) = 45.
Направление поиска:
p1 = [1;0]T
p2 = [0;1]T
Шаг №1. Сделаем шаг вдоль направления поиска p2 = [0;1]T
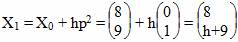
f(X1) = 4(8-5)2+((h+9)-6)2 → min
f(X1) = h2+6h+45 → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x1)=0):
2h+6 = 0. Получим шаг: h = -3
Выполнение этого шага приведет в точку:
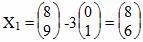
Шаг №2. Сделаем шаг вдоль другого направления поиска p1 = [1;0]T
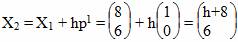
f(X2) = 4((h+8)-5)2+((6)-6)2 → min
f(X2) = 4h2+24h+36 → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x2)=0):
8h+24 = 0. Получим шаг: h = -3
Выполнение этого шага приведет в точку:
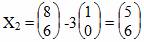
Шаг №3. Повторно сделаем шаг вдоль направления поиска p2 = [0;1]T 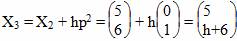
f(X3) = 4(5-5)2+((h+6)-6)2 → min
f(X3) = h2 → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x3)=0):
2h = 0. Получим шаг: h = 0
Выполнение этого шага приведет в точку:
Шаг №4. Выбираем сопряженное направление: p2 = x3 - x1
p2 = [5;6]T - [8;6]T = [-3;0]T
Итерация №1.
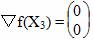
Проверим критерий остановки:
|▽f(X3)| < ε
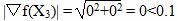
Вычислим значение функции в начальной точке f(X3) = 0.
Ответ: X = [5;6]T
Пример №2. Минимизировать функцию f(x) методом сопряженных направлений, заканчивая вычисления при |d(x)/dx| < 10-3, i=1,2,..,n.
x14+2*x24+x12*x22+2*x1+x2
Градиент функции
| ▽ f(X) = |
|
Итерация №0.
| ▽ f(X0) = |
|
Проверим критерий остановки:
|▽f(X0)| < ε
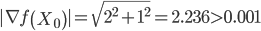
Вычислим значение функции в начальной точке f(X0) = 0.
Направление поиска:
p1 = [1;0]T
p2 = [0;1]T
Шаг №1. Сделаем шаг вдоль направления поиска p2 = [0;1]T
| X1 = X0 + hp2 = |
| + h |
| = |
|
f(X1) = (0)4+2*(h)4+(0)2*(h)2+2*(0)+(h) → min
f(X1) = 2.0*h4+h → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x1)=0):
8.0*h3+1.0 = 0
Получим шаг: h = -0.5
Выполнение этого шага приведет в точку:
| X1 = |
| -0.5 |
| = |
|
Шаг №2. Сделаем шаг вдоль другого направления поиска p1 = [1;0]T
| X2 = X1 + hp1 = |
| + h |
| = |
|
f(X2) = (h)4+2*(-0.5)4+(h)2*(-0.5)2+2*(h)+(-0.5) → min
f(X2) = h4+0.25*h2+2.0*h-0.375 → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x2)=0):
4.0*h3+0.5*h+2.0 = 0
Получим шаг: h = -0.7413
Выполнение этого шага приведет в точку:
| X2 = |
| -0.7413 |
| = |
|
Шаг №3. Повторно сделаем шаг вдоль направления поиска p2 = [0;1]T
| X3 = X2 + hp2 = |
| + h |
| = |
|
f(X3) = (-0.74129)4+2*(h-0.5)4+(-0.74129)2*(h-0.5)2+2*(-0.74129)+(h-0.5) → min
f(X3) = 2.0*h4-4.0*h3+3.5495*h2-0.5495*h-1.4182 → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x3)=0):
8.0*h3-12.0*h2+7.099*h-0.5495 = 0
Получим шаг: h = 0.09038
Выполнение этого шага приведет в точку:
| X3 = |
| + 0.09038 |
| = |
|
Ответ: X = [-0.7413;-0.4096]T
Итерация №1.
| ▽ f(X3) = |
|
Проверим критерий остановки:
|▽f(X3)| < ε

Вычислим значение функции в новой точке f(X3) = -1.442.
Направление поиска:
p1 = [1;0]T
p2 = [-0.741;0.0904]T
Шаг №1. Сделаем шаг вдоль направления поиска p2 = [-0.741;0.0904]T
| X4 = X3 + hp2 = |
| + h |
| = |
|
f(X4) = (-0.7413*h-0.7413)4+2*(0.0904*h-0.4096)4+(-0.7413*h-0.7413)2*(0.0904*h-0.4096)2+2*(-0.7413*h-0.7413)+(0.0904*h-0.4096) → min
f(X4) = 0.3066*h4+1.1738*h3+1.8436*h2-0.090289*h-1.4417 → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x4)=0):
1.2264*h3+3.5213*h2+3.6872*h-0.090289 = 0
Получим шаг: h = 0.02394
Выполнение этого шага приведет в точку:
| X4 = |
| + 0.02394 |
| = |
|
Шаг №2. Сделаем шаг вдоль другого направления поиска p1 = [1;0]T
| X5 = X4 + hp1 = |
| + h |
| = |
|
f(X5) = (h-0.75904)4+2*(-0.40744)4+(h-0.75904)2*(-0.40744)2+2*(h-0.75904)+(-0.40744) → min
f(X5) = h4-3.0362*h3+3.6229*h2-0.0012937*h-1.4428 → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x5)=0):
0.33201*h+4.0*(h-0.75904)3+1.748 = 0
Получим шаг: h = 0.000178
Выполнение этого шага приведет в точку:
| X5 = |
| + 0.000178 |
| = |
|
Шаг №3. Повторно сделаем шаг вдоль направления поиска p2 = [-0.741;0.0904]T
| X6 = X5 + hp2 = |
| + h |
| = |
|
f(X6) = (-0.7413*h-0.75887)4+2*(0.0904*h-0.40744)4+(-0.7413*h-0.75887)2*(0.0904*h-0.40744)2+2*(-0.7413*h-0.75887)+(0.0904*h-0.40744) → min
f(X6) = 0.3066*h4+1.2028*h3+1.9281*h2-0.00093611*h-1.4428 → min
Найдем такой шаг h, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(x6)=0):
1.2264*h3+3.6085*h2+3.8562*h-0.00093611 = 0
Получим шаг: h = 0.000243
Выполнение этого шага приведет в точку:
| X6 = |
| + 0.000243 |
| = |
|
Ответ: X = [-0.759;-0.4074]T
Итерация №2.
| ▽ f(X6) = |
|
Проверим критерий остановки:
|▽f(X6)| < ε
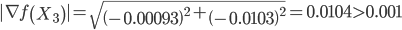
Вычислим значение функции в новой точке f(X6) = -1.443.
Направление поиска: p1 = [1;0]T, p2 = [0;0]T
Одно из направлений поиска p2 = [0;0]T. Заканчиваем процесс итераций.
Ответ: X = [-0.759;-0.4074]T



