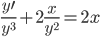Применение формул комбинаторики к вычислению вероятностей
В партии из S изделий имеется T нестандартных. Определите вероятность того, что среди выбранных наудачу s изделий нестандартными окажутся t изделий.Решение. Элементарным исходом является выборка любых s изделий из их общего числа S. Число всех таких исходов равно числу сочетаний из S по s, то есть n = CsS. Интересующее нас событие A — это извлечение s изделий, в которых s – t изделий — качественные, а t — нестандартные. Число таких групп
способами, причем любая группа исправных изделий может комбинироваться с любой группой нестандартных изделий. Отсюда
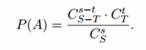
Задачи подобного типа решаются с помощью калькулятора (пример 3).
Пример №1. В команде участников студенческой олимпиады 4 девушки и 6 юношей. Разыгрываются 3 диплома первой степени. Какова вероятность того, что среди обладателей дипломов окажутся одна девушка и двое юношей?
Решение. Число всех равновозможных случаев распределения 3 дипломов среди 10 человек равно числу сочетаний C310. Число групп по двое юношей из шести, которые могут получить дипломы — C26. Каждая пара может сочетаться с любой девушкой, число таких выборов — C14. Следовательно, число групп: двое юношей и одна девушка равно произведению 
. Это число благоприятствующих случаев распределения дипломов. Искомая вероятность:
Пример №2. На складе университета хранится 28 одинаковых упаковок писчей бумаги. Известно, что в четырех из них содержится бумага более низкого качества. Случайным образом выбирают три упаковки бумаги, Вычислить вероятность того, что среди них;
А) нет упаковок с бумагой более низкого качества,
Б) есть одна упаковка такой бумаги.
Решение.
Рассмотрим два случайных события:
А – среди взятых трех упаковок нет упаковок с бумагой более низкого качества;
В - среди взятых трех упаковок есть одна упаковка с бумагой более низкого качества (и, следовательно, две – с бумагой более высокого качества).
Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 3 упаковки бумаги из 28 упаковок, то есть
– числу сочетаний из 28 элементов по 3.
б) Подсчитаем число исходов, благоприятствующих данному событию (среди трех упаковок бумаги ровно 1 упаковка содержит бумагу более низкого качества): две упаковки можно выбрать из 24 упаковок:
способами, при этом одну упаковку нужно выбирать из четырех: 
способами. Следовательно, число благоприятствующих исходов равно
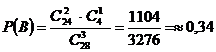
Ответ: а)Р(А) =0,62;б) Р(В)=0,34.
Пример №3. В коробке 30 одинаковых юбилейных монет. Известно, что 5 из них имеют нестандартный процент содержания золота. Случайным образом выбирают три монеты. Вычислите вероятность того, что: а). Все монеты имеют нестандартный процент содержания золота; б). Только одна монета имеет нестандартный процент содержания золота.
Решение:
Рассмотрим два случайных события:
А – среди взятых трех монет все монеты имеют нестандартный процент содержания золота;
В - среди взятых трех монет одна монета имеет нестандартный процент содержания золота.
Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 3 монеты из 30, то есть
– числу сочетаний из 30 элементов по 3.
искомая вероятность равна отношению числа исходов, благоприятствующих событию А, к числу всех элементарных исходов:
б) Подсчитаем число исходов, благоприятствующих данному событию (среди трех монет ровно 1 монета имеет нестандартный процент содержания золота): две монеты можно выбрать из 25 монет:
способами, при этом одну монету нужно выбирать из 5:
способами. Следовательно,число благоприятствующих исходов равно 
Искомая вероятность равна отношению числа исходов, благоприятствующих событию В, к числу всех элементарных исходов
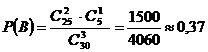
Ответ: а)Р(А) =0,00246;б) Р(В)=0,37.
Аналогичные примеры задач (задачи подобного типа решаются с помощью калькулятора (пример 3)).
- В ящике имеется 10 деталей, среди которых 7 окрашенных. Рабочий наугад извлекает 4 детали. Найти вероятность того, что среди извлеченных деталей окажутся ровно две окрашенные детали.
- В ноябре обычно бывает 18 морозных дней какова вероятность того что среди шести случайно выбранных ноябрьских дней окажется хотя бы 2 морозных?
Примечание: В ноябре 30 дней, из низ 18 морозных (бракованных). В калькуляторе рассчитываются вероятности для всех 6 дней, поэтому для ответ необходимо взятьP(2)+P(3)+P(4)+P(5)+P(6)или1-P(0)-P(1).
