Уравнение регрессии в стандартизованном виде
Задание.- Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
- Дайте экономическую интерпретацию параметров модели.
- Рассчитайте стандартизованные коэффициенты модели и запишите уравнение регрессии в стандартизованном виде. Верно ли утверждение, что цена блага оказывает большее влияние на объем предложения блага, чем заработная плата сотрудников?
- Для полученной модели (в естественной форме) проверьте выполнение условия гомоскедастичности остатков, применив тест Голдфельда-Квандта.
- Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
- Проверьте, адекватно ли предположение об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки (по первым 8 и остальным 8 наблюдениям) в одну и рассматривать единую модель регрессии Y по X?
1. Оценка уравнения регрессии. Определим вектор оценок коэффициентов регрессии с помощью сервиса Уравнение множественной регрессии
. Согласно методу наименьших квадратов, вектор s получается из выражения: s = (XTX)-1XTY
Матрица X
| 1 | 182.94 | 1018 |
| 1 | 193.45 | 920 |
| 1 | 160.09 | 686 |
| 1 | 157.99 | 405 |
| 1 | 123.83 | 683 |
| 1 | 152.02 | 530 |
| 1 | 130.53 | 525 |
| 1 | 137.38 | 418 |
| 1 | 137.58 | 425 |
| 1 | 118.78 | 161 |
| 1 | 142.9 | 242 |
| 1 | 99.49 | 226 |
| 1 | 116.17 | 162 |
| 1 | 185.66 | 70 |
| 4.07 |
| 4 |
| 2.98 |
| 2.2 |
| 2.83 |
| 3 |
| 2.35 |
| 2.04 |
| 1.97 |
| 1.02 |
| 1.44 |
| 1.22 |
| 1.11 |
| 0.82 |
Матрица XT
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 182.94 | 193.45 | 160.09 | 157.99 | 123.83 | 152.02 | 130.53 | 137.38 | 137.58 | 118.78 | 142.9 | 99.49 | 116.17 | 185.66 |
| 1018 | 920 | 686 | 405 | 683 | 530 | 525 | 418 | 425 | 161 | 242 | 226 | 162 | 70 |
| XT X = |
|
В матрице, (XTX) число 14, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы XT и 1-го столбца матрицы X
Умножаем матрицы, (XTY)
| XT Y = |
|
Находим обратную матрицу (XTX)-1
| 2.25 | -0.0161 | 0.00037 |
| -0.0161 | 0.000132 | -7.0E-6 |
| 0.00037 | -7.0E-6 | 1.0E-6 |
| Y(X) = |
| * |
| = |
|
Уравнение регрессии (оценка уравнения регрессии)
Y = 0.18 + 0.00297X1 + 0.00347X2
2. Матрица парных коэффициентов корреляции R. Число наблюдений n = 14. Число независимых переменных в модели равно 2, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 4. Матрица, независимых переменных Х имеет размерность (14 х 4).
Матрица, составленная из Y и X:
| 1 | 4.07 | 182.94 | 1018 |
| 1 | 4 | 193.45 | 920 |
| 1 | 2.98 | 160.09 | 686 |
| 1 | 2.2 | 157.99 | 405 |
| 1 | 2.83 | 123.83 | 683 |
| 1 | 3 | 152.02 | 530 |
| 1 | 2.35 | 130.53 | 525 |
| 1 | 2.04 | 137.38 | 418 |
| 1 | 1.97 | 137.58 | 425 |
| 1 | 1.02 | 118.78 | 161 |
| 1 | 1.44 | 142.9 | 242 |
| 1 | 1.22 | 99.49 | 226 |
| 1 | 1.11 | 116.17 | 162 |
| 1 | 0.82 | 185.66 | 70 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4.07 | 4 | 2.98 | 2.2 | 2.83 | 3 | 2.35 | 2.04 | 1.97 | 1.02 | 1.44 | 1.22 | 1.11 | 0.82 |
| 182.94 | 193.45 | 160.09 | 157.99 | 123.83 | 152.02 | 130.53 | 137.38 | 137.58 | 118.78 | 142.9 | 99.49 | 116.17 | 185.66 |
| 1018 | 920 | 686 | 405 | 683 | 530 | 525 | 418 | 425 | 161 | 242 | 226 | 162 | 70 |
| 14 | 31.05 | 2038.81 | 6471 |
| 31.05 | 83.37 | 4737.04 | 18230.79 |
| 2038.81 | 4737.04 | 307155.61 | 995591.55 |
| 6471 | 18230.79 | 995591.55 | 4062413 |
| ∑n | ∑y | ∑x1 | ∑x2 |
| ∑y | ∑y2 | ∑x1 y | ∑x2 y |
| ∑x1 | ∑yx1 | ∑x1 2 | ∑x2 x1 |
| ∑x2 | ∑yx2 | ∑x1 x2 | ∑x2 2 |
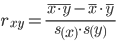
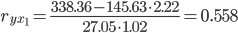
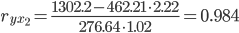
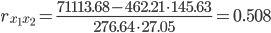
| Признаки x и y | ∑xi | 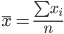 | ∑yi | 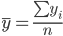 | ∑xiyi | 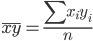 |
| Для y и x1 | 2038.81 | 145.629 | 31.05 | 2.218 | 4737.044 | 338.36 |
| Для y и x2 | 6471 | 462.214 | 31.05 | 2.218 | 18230.79 | 1302.199 |
| Для x1 и x2 | 6471 | 462.214 | 2038.81 | 145.629 | 995591.55 | 71113.682 |
| Признаки x и y | 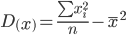 | 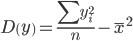 | 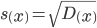 | 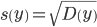 |
| Для y и x1 | 731.797 | 1.036 | 27.052 | 1.018 |
| Для y и x2 | 76530.311 | 1.036 | 276.641 | 1.018 |
| Для x1 и x2 | 76530.311 | 731.797 | 276.641 | 27.052 |
Матрица парных коэффициентов корреляции R:
| - | y | x1 | x2 |
| y | 1 | 0.558 | 0.984 |
| x1 | 0.558 | 1 | 0.508 |
| x2 | 0.984 | 0.508 | 1 |
- связь между результативным признаком и факторным должна быть выше межфакторной связи;
- связь между факторами должна быть не более 0.7. Если в матрице есть межфакторный коэффициент корреляции rxjxi > 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.;
- при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними.
В нашем случае все парные коэффициенты корреляции |r|<0.7, что говорит об отсутствии мультиколлинеарности факторов.
Модель регрессии в стандартном масштабе
Модель регрессии в стандартном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам: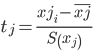
где хji - значение переменной хji в i-ом наблюдении.
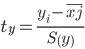
Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение S.
Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:
ty = ∑βjtxj
Для оценки β-коэффициентов применим МНК. При этом система нормальных уравнений будет иметь вид:
rx1y=β1+rx1x2•β2 + ... + rx1xm•βm
rx2y=rx2x1•β1 + β2 + ... + rx2xm•βm
...
rxmy=rxmx1•β1 + rxmx2•β2 + ... + βm
Для наших данных (берем из матрицы парных коэффициентов корреляции):
0.558 = β1 + 0.508β2
0.984 = 0.508β1 + β2
Данную систему линейных уравнений решаем методом Гаусса: β1 = 0.0789; β2 = 0.944;
Стандартизированная форма уравнения регрессии имеет вид:
y0 = 0.0789x1 + 0.944x2
Найденные из данной системы β–коэффициенты позволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам:
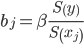
a=y-∑bj·xj
Стандартизированные частные коэффициенты регрессии. Стандартизированные частные коэффициенты регрессии - β-коэффициенты (βj) показывают, на какую часть своего среднего квадратического отклонения S(у) изменится признак-результат y с изменением соответствующего фактора хj на величину своего среднего квадратического отклонения (Sхj) при неизменном влиянии прочих факторов (входящих в уравнение).
По максимальному βj можно судить, какой фактор сильнее влияет на результат Y.
По коэффициентам эластичности и β-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
Коэффициент βj может также интерпретироваться как показатель прямого (непосредственного) влияния j-ого фактора (xj) на результат (y). Во множественной регрессии j-ый фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели).
Косвенное влияние измеряется величиной: ∑βirxj,xi, где m - число факторов в модели. Полное влияние j-ого фактора на результат равное сумме прямого и косвенного влияний измеряет коэффициент линейной парной корреляции данного фактора и результата - rxj,y.
Так для нашего примера непосредственное влияние фактора x1 на результат Y в уравнении регрессии измеряется βj и составляет 0.0789; косвенное (опосредованное) влияние данного фактора на результат определяется как:
rx1x2β2 = 0.508 * 0.944 = 0.4796
Пример №2. Покажем пример нахождения стандартизованных коэффициентов с помощью калькулятора.
Уравнение множественной регрессии может быть представлено в виде:
Y = f(β , X) + ε
где X = X(X1, X2, ..., Xm) - вектор независимых (объясняющих) переменных; β - вектор параметров (подлежащих определению); ε - случайная ошибка (отклонение); Y - зависимая (объясняемая) переменная.
теоретическое линейное уравнение множественной регрессии имеет вид:
Y = β0 + β1X1 + β2X2 + ... + βmXm + ε
β0 - свободный член, определяющий значение Y, в случае, когда все объясняющие переменные Xj равны 0.
Прежде чем перейти к определению нахождения оценок коэффициентов регрессии, необходимо проверить ряд предпосылок МНК.
Предпосылки МНК:
1. Математическое ожидание случайного отклонения εi равно 0 для всех наблюдений (M(εi) = 0).
2. Гомоскедастичность (постоянство дисперсий отклонений). Дисперсия случайных отклонений εi постоянна: D(εi) = D(εj) = S2 для любых i и j.
3. отсутствие автокорреляции.
4. Случайное отклонение должно быть независимо от объясняющих переменных: Yeixi = 0.
5. Модель является линейное относительно параметров.
6. отсутствие мультиколлинеарности. Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость.
7. Ошибки εi имеют нормальное распределение. Выполнимость данной предпосылки важна для проверки статистических гипотез и построения доверительных интервалов.
Эмпирическое уравнение множественной регрессии представим в виде:
Y = b0 + b1X1 + b1X1 + ... + bmXm + e
Здесь b0, b1, ..., bm - оценки теоретических значений β0, β1, β2, ..., βm коэффициентов регрессии (эмпирические коэффициенты регрессии); e - оценка отклонения ε.
При выполнении предпосылок МНК относительно ошибок εi, оценки b0, b1, ..., bm параметров β0, β1, β2, ..., βm множественной линейной регрессии по МНК являются несмещенными, эффективными и состоятельными (т.е. BLUE-оценками).
Для оценки параметров уравнения множественной регрессии применяют МНК.
1. Оценка уравнения регрессии.
Матрица парных коэффициентов корреляции.
| - | y | x1 | x2 | x3 |
| y | 1 | 0.91 | 0.87 | 0.25 |
| x1 | 0.91 | 1 | 0.96 | 0.27 |
| x2 | 0.87 | 0.96 | 1 | 0.3 |
| x3 | 0.25 | 0.27 | 0.3 | 1 |
Коллинеарность – зависимость между факторами. В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:
r(xjy) > r(xkxj) ; r(xky) > r(xkxj).
Если одно из неравенств не соблюдается, то исключается тот параметр xk или xj, связь которого с результативным показателем Y оказывается наименее тесной.
При оценке мультиколлинеарности факторов следует учитывать, что чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии.
Для отбора наиболее значимых факторов xi учитываются следующие условия:
- связь между результативным признаком и факторным должна быть выше межфакторной связи;
- связь между факторами должна быть не более 0.7;
- при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними.
Более объективную характеристику тесноты связи дают частные коэффициенты корреляции, измеряющие влияние на результат фактора xi при неизменном уровне других факторов.
Модель регрессии в стандартном масштабе.
Модель регрессии в стандартном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам:
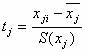
где хji - значение переменной хji в i-ом наблюдении.
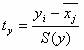
Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение S.
Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:
ty = ∑βjtxj
Для оценки β-коэффициентов применим МНК. При этом система нормальных уравнений будет иметь вид:
rx1y=β1+rx1x2•β2 + ... + rx1xm•βm
rx2y=rx2x1•β1 + β2 + ... + rx2xm•βm
...
rxmy=rxmx1•β1 + rxmx2•β2 + ... + βm
Для наших данных:
0.909753132158 = β1 + 0.964334224566β2 + 0.266609783368β3
0.871599975524 = 0.964334224566β1 + β2 + 0.303816910883β3
0.248833984737 = 0.266609783368β1 + 0.303816910883β2 + β3
Откуда находим: β1 = 0.99252522540571; β2 = -0.088940575270852; β3 = 0.011238700231903;
Стандартизированная форма уравнения регрессии имеет вид:
y0 = 0.993x1 -0.0889x2 + 0.0112x3
Найденные из данной системы β–коэффициенты позволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам:
a=y-∑bj·xj
3. Анализ параметров уравнения регрессии.
Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительных ошибок аппроксимации
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка ε = Y - Y(x) = Y - X*s (абсолютная ошибка аппроксимации)
| Y | Y(x) | ε | (Y-Y)2 |
| 360 | 353.38 | 6.62 | 900 |
| 298 | 314.13 | -16.13 | 1024 |
| 328 | 329.68 | -1.68 | 4 |
| 330 | 332.79 | -2.79 | 0 |
| 366 | 370.25 | -4.25 | 1296 |
| 316 | 310.92 | 5.08 | 196 |
| 334 | 320.45 | 13.55 | 16 |
| 300 | 315.52 | -15.52 | 900 |
| 314 | 317.88 | -3.88 | 256 |
| 320 | 308.78 | 11.22 | 100 |
| 362 | 361.89 | 0.11 | 1024 |
| 332 | 324.34 | 7.66 | 4 |
| 5720 |
Несмещенная оценка дисперсии равна:
Оценка среднеквадратичного отклонения равна (стандартная ошибка для оценки Y):
Найдем оценку ковариационной матрицы вектора k = S • (XTX)-1
| 462.04 | -61.95 | 1199.68 | -1.72 |
| -61.95 | 9.02 | -187.38 | 0.14 |
| 1199.68 | -187.38 | 4208.43 | -5.42 |
| -1.72 | 0.14 | -5.42 | 0.21 |
Показатели тесноты связи факторов с результатом.
Если факторные признаки различны по своей сущности и (или) имеют различные единицы измерения, то коэффициенты регрессии bj при разных факторах являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат.
К таким показателям тесноты связи относят: частные коэффициенты эластичности, β–коэффициенты, частные коэффициенты корреляции.
Частные коэффициенты эластичности.
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле:
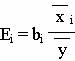
Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется признак-результат у с увеличением признака-фактора хj на 1% от своего среднего уровня при фиксированном положении других факторов модели.
![]()
Частный коэффициент эластичности |E1| < 1. Следовательно, его влияние на результативный признак Y незначительно.
![]()
Частный коэффициент эластичности |E2| < 1. Следовательно, его влияние на результативный признак Y незначительно.
![]()
Частный коэффициент эластичности |E3| < 1. Следовательно, его влияние на результативный признак Y незначительно.
Стандартизированные частные коэффициенты регрессии.
Стандартизированные частные коэффициенты регрессии - β-коэффициенты (βj) показывают, на какую часть своего среднего квадратического отклонения S(у) изменится признак-результат y с изменением соответствующего фактора хj на величину своего среднего квадратического отклонения (Sхj) при неизменном влиянии прочих факторов (входящих в уравнение).
По максимальному βj можно судить, какой фактор сильнее влияет на результат Y.
По коэффициентам эластичности и β-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
Коэффициент βj может также интерпретироваться как показатель прямого (непосредственного) влияния j-ого фактора (xj) на результат (y). Во множественной регрессии j-ый фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели).
Косвенное влияние измеряется величиной: ∑βirxj,xi, где m - число факторов в модели. Полное влияние j-ого фактора на результат равное сумме прямого и косвенного влияний измеряет коэффициент линейной парной корреляции данного фактора и результата - rxj,y.
Так для нашего примера непосредственное влияние фактора x1 на результат Y в уравнении регрессии измеряется βj и составляет 0.99252522540571; косвенное (опосредованное) влияние данного фактора на результат определяется как:
rx1x2β2 = 0.964334224566*(-0.088940575270852)=-0.08577
Частные коэффициенты корреляции.
Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и xi) при условии, что влияние на них остальных факторов (xj) устранено.
![]()
![]()
Теснота связи умеренная
![]()
![]()
Теснота связи сильная
![]()
![]()
Теснота связи низкая.
![]()
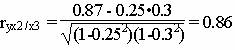
Теснота связи сильная
![]()
![]()
Теснота связи низкая.
![]()
![]()
Теснота связи низкая.
![]()
![]()
Теснота связи сильная
![]()
![]()
Теснота связи сильная
![]()
![]()
Теснота связи низкая.
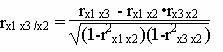
![]()
Теснота связи низкая.
![]()
![]()
Теснота связи низкая.
![]()
![]()
Теснота связи низкая.
Индекс множественной корреляции (множественный коэффициент корреляции).
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции.
В отличии от парного коэффициента корреляции, который может принимать отрицательные значения, он принимает значения от 0 до 1.
Поэтому R не может быть использован для интерпретации направления связи. Чем плотнее фактические значения yi располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина Ry(x1,...,xm).
Таким образом, при значении R близком к 1, уравнение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат. При значении R близком к 0 уравнение регрессии плохо описывает фактические данные и факторы оказывают слабое воздействие на результат.
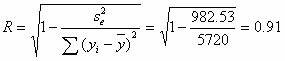
Связь между признаком Y факторами X сильная
Значимость коэффициента корреляции.
![]()
По таблице Стьюдента находим Tтабл
Tкрит(n-m-1;α/2) = (8;0.025) = 2.306
Поскольку Tнабл > Tкрит , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Коэффициент детерминации.
R2= 0.912 = 0.83
т.е. в 82.83 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая
4. Оценка значения результативного признака при заданных значениях факторов.
Y(0.0,0.0,0.0,) = 94.78 + 17.82 * 0.0-34.11 * 0.0 + 0.11 * 0.0 = 94.78
Доверительные интервалы с вероятностью 0.95 для среднего значения результативного признака M(Y).
S2 = X0T(XTX)-1X0
где
X0T = [ 1 ; 0.0 ; 0.0 ; 0.0]
(XTX)-1
| 41.69 | -5.59 | 108.25 | -0.16 |
| -5.59 | 0.81 | -16.91 | 0.0129 |
| 108.25 | -16.91 | 379.74 | -0.49 |
| -0.16 | 0.0129 | -0.49 | 0.0188 |
X0
| 1 |
| 0 |
| 0 |
| 0 |
(Y – t*SY ; Y + t*SY )
(94.78 – 2.306*71.56 ; 94.78 + 2.306*71.56)
(-70.24;259.8)
C вероятностью 0.95 среднее значение Y при X0i находится в указанных пределах.
Доверительные интервалы с вероятностью 0.95 для индивидуального значения результативного признака.
(94.78 – 2.306*72.41 ; 94.78 + 2.306*72.41)
(-72.2;261.76)
C вероятностью 0.95 индивидуальное значение Y при X0i находится в указанных пределах.
5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
v = n - m - 1 называется числом степеней свободы. Считается, что при оценивании множественной линейной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений, по крайней мере, в 3 раза превосходило число оцениваемых параметров.
1) t-статистика
Tтабл (n-m-1;α) = (8;0.025) = 2.306
Находим стандартную ошибку коэффициента регрессии b0:
Статистическая значимость коэффициента регрессии b0 подтверждается.
Находим стандартную ошибку коэффициента регрессии b1:
Статистическая значимость коэффициента регрессии b1 подтверждается.
Находим стандартную ошибку коэффициента регрессии b2:
Статистическая значимость коэффициента регрессии b2 не подтверждается.
Находим стандартную ошибку коэффициента регрессии b3:
Статистическая значимость коэффициента регрессии b3 не подтверждается.
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(bi - ti Sbi; bi + ti Sbi)
b0: (94.78 - 2.306 • 21.5 ; 94.78 + 2.306 • 21.5) = (45.21;144.35)
b1: (17.82 - 2.306 • 3 ; 17.82 + 2.306 • 3) = (10.9;24.75)
b2: (-34.11 - 2.306 • 64.87 ; -34.11 + 2.306 • 64.87) = (-183.7;115.49)
b3: (0.11 - 2.306 • 0.46 ; 0.11 + 2.306 • 0.46) = (-0.94;1.16)
6. Проверка общего качества уравнения множественной регрессии.
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности: R2 или b1 = b2 =... = bm = 0 (гипотеза о незначимости уравнения регрессии, рассчитанного по данным генеральной совокупности).
Для ее проверки используют F-критерий Фишера.
При этом вычисляют фактическое (наблюдаемое) значение F-критерия, через коэффициент детерминации R2, рассчитанный по данным конкретного наблюдения.
По таблицам распределения Фишера-Снедоккора находят критическое значение F-критерия (Fкр). Для этого задаются уровнем значимости α (обычно его берут равным 0,05) и двумя числами степеней свободы k1=m и k2=n-m-1.
2) F-статистика. Критерий Фишера
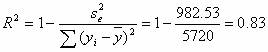
Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение Y.
Более объективной оценкой является скорректированный коэффициент детерминации:
Добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.
Проверим гипотезу об общей значимости - гипотезу об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:
H0: β1 = β2 = ... = βm = 0.
Проверка этой гипотезы осуществляется с помощью F-статистики распределения Фишера.
Если F < Fkp = Fα ; n-m-1, то нет оснований для отклонения гипотезы H0.
Табличное значение при степенях свободы k1 = 3 и k2 = n-m-1 = 12 - 3 -1 = 8, Fkp(3;8) = 4.07
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
Оценка значимости дополнительного включения фактора (частный F-критерий).
Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличить долю объясненной вариации результативного признака. Это может быть связано с последовательностью вводимых факторов (т. к. существует корреляция между самими факторами).
Мерой оценки значимости улучшения качества модели, после включения в нее фактора хj, служит частный F-критерий – Fxj:
где m – число оцениваемых параметров.
В числителе - прирост доли вариации у за счет дополнительно включенного в модель фактора хj.
Если наблюдаемое значение Fxj больше Fkp, то дополнительное введение фактора xj в модель статистически оправдано.
Частный F-критерий оценивает значимость коэффициентов «чистой» регрессии (bj). Существует взаимосвязь между частным F-критерием - Fxj и t-критерием, используемым для оценки значимости коэффициента регрессии при j-м факторе:
7. Проверка на наличие гетероскедастичности.
1) Методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной Xi, а по оси ординат квадраты отклонения εi2.
Если имеется определенная связь между отклонениями, то гетероскедастичность имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии гетероскедастичности.
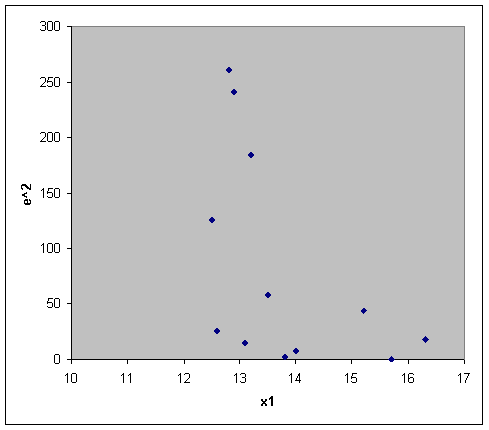
Как видим, особой зависимости не наблюдается.
2) При помощи теста ранговой корреляции Спирмена.
Тест ранговой корреляции Спирмена
Задаются два параметра: xi, ε.
| y | y(x) | ε = y-y(x) | ε2 |
| 360 | 353.38 | 6,62 | 43,79 |
| 298 | 314.13 | -16,13 | 260,21 |
| 328 | 329.68 | -1,68 | 2,84 |
| 330 | 332.79 | -2,79 | 7,77 |
| 366 | 370.25 | -4,25 | 18,04 |
| 316 | 310.92 | 5,08 | 25,85 |
| 334 | 320.45 | 13,55 | 183,7 |
| 300 | 315.52 | -15,52 | 240,73 |
| 314 | 317.88 | -3,88 | 15,06 |
| 320 | 308.78 | 11,22 | 125,82 |
| 362 | 361.89 | 0,11 | 0,0128 |
| 332 | 324.34 | 7,66 | 58,71 |
Коэффициент ранговой корреляции Спирмена.
Присвоим ранги признаку ε и фактору x1. Найдем сумму разности квадратов d2.
По формуле вычислим коэффициент ранговой корреляции Спирмена.
| x1 | ε | ранг x1, dx | ранг ε, dy | (dx - dy)2 |
| 15.2 | 6.62 | 10 | 9 | 1 |
| 12.8 | -16.13 | 3 | 1 | 4 |
| 13.8 | -1.68 | 8 | 6 | 4 |
| 14 | -2.79 | 9 | 5 | 16 |
| 16.3 | -4.25 | 12 | 3 | 81 |
| 12.6 | 5.08 | 2 | 8 | 36 |
| 13.2 | 13.55 | 6 | 12 | 36 |
| 12.9 | -15.52 | 4 | 2 | 4 |
| 13.1 | -3.88 | 5 | 4 | 1 |
| 12.5 | 11.22 | 1 | 11 | 100 |
| 15.7 | 0.11 | 11 | 7 | 16 |
| 13.5 | 7.66 | 7 | 10 | 9 |
| 308 |
Связь между признаком ε и фактором x1 слабая и обратная
Оценка коэффициента ранговой корреляции Спирмена.
Значимость коэффициента ранговой корреляции Спирмена
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена при конкурирующей гипотезе Hi. p ≠ 0, надо вычислить критическую точку:
где n - объем выборки; p - выборочный коэффициент ранговой корреляции Спирмена: t(α, к) - критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента, по уровню значимости α и числу степеней свободы k = n-2.
Если |p| < Тkp - нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками не значима. Если |p| > Tkp - нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.
По таблице Стьюдента находим t(α, k):
t(α, k) = (10;0.05) = 1.812
Поскольку Tkp > p, то принимаем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически - не значим и ранговая корреляционная связь между оценками по двум тестам незначимая. Для нашего анализа это свидетельствует об отсутствии гетероскедастичности.
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения εi с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения εi (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии автокорреляции.
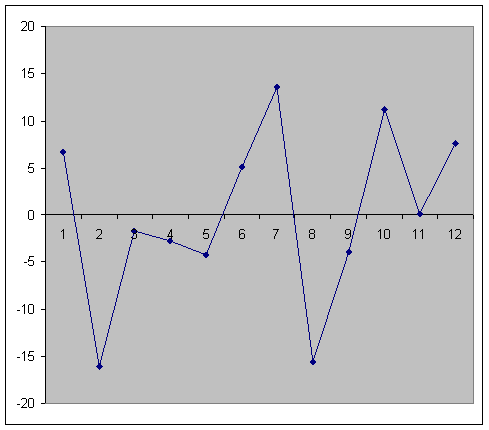
2. Коэффициент автокорреляции.
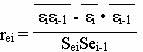
Если коэффициент автокорреляции rei < 0.5, то есть основания утверждать, что автокорреляция отсутствует.
3. Критерий Дарбина-Уотсона.
Этот критерий является наиболее известным для обнаружения автокорреляции.
При статистическом анализе уравнения регрессии на начальном этапе часто проверяют выполнимость одной предпосылки: условия статистической независимости отклонений между собой. При этом проверяется некоррелированность соседних величин ei.
| y | y(x) | ei = y-y(x) | e2 | (ei - ei-1)2 |
| 360 | 353.38 | 6.62 | 43.79 | 0 |
| 298 | 314.13 | -16.13 | 260.21 | 517.47 |
| 328 | 329.68 | -1.68 | 2.84 | 208.7 |
| 330 | 332.79 | -2.79 | 7.77 | 1.22 |
| 366 | 370.25 | -4.25 | 18.04 | 2.13 |
| 316 | 310.92 | 5.08 | 25.85 | 87.08 |
| 334 | 320.45 | 13.55 | 183.7 | 71.73 |
| 300 | 315.52 | -15.52 | 240.73 | 845.01 |
| 314 | 317.88 | -3.88 | 15.06 | 135.35 |
| 320 | 308.78 | 11.22 | 125.82 | 227.96 |
| 362 | 361.89 | 0.11 | 0.0128 | 123.29 |
| 332 | 324.34 | 7.66 | 58.71 | 56.99 |
| 982.53 | 2276.94 |
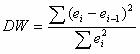
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости α, числа наблюдений n = 12 и количества объясняющих переменных m=3.
Автокорреляция отсутствует, если выполняется следующее условие:
d1 < DW и d2 < DW < 4 - d2.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 < DW < 2.5. Поскольку 1.5 < 2.32 < 2.5, то автокорреляция остатков отсутствует.
Для более надежного вывода целесообразно обращаться к табличным значениям.
По таблице Дарбина-Уотсона для n=12 и k=3 (уровень значимости 5%) находим: d1 = 0.82; d2 = 1.75.
Поскольку 0.82 < 2.32 и 1.75 < 2.32 < 4 - 1.75, то автокорреляция остатков присутствует.