Уравнение множественной регрессии
Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.Назначение сервиса. С помощью онлайн-калькулятора можно найти следующие показатели:
- уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
- множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;
Отбор факторов обычно осуществляется в два этапа:
- теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
- количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа - однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.
- Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
- Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
- Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность - тесная линейная связь между факторами.
Пример. Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X
| 1 | 5 | 14.5 |
| 1 | 12 | 18 |
| 1 | 6 | 12 |
| 1 | 7 | 13 |
| 1 | 8 | 14 |
Матрица Y
| 9 |
| 13 |
| 16 |
| 14 |
| 21 |
Транспонируем матрицу X, получаем XT:
| 1 | 1 | 1 | 1 | 1 |
| 5 | 12 | 6 | 7 | 8 |
| 14.5 | 18 | 12 | 13 | 14 |
| Умножаем матрицы, XT X = |
|
В матрице, (XTX) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы XT и 1-го столбца матрицы X
| Умножаем матрицы, XT Y = |
|
Находим обратную матрицу (XTX)-1
| 13.99 | 0.64 | -1.3 |
| 0.64 | 0.1 | -0.0988 |
| -1.3 | -0.0988 | 0.14 |
Вектор оценок коэффициентов регрессии равен
(XTX)-1XTY = y(x) = |
| * |
| = |
|
Получили оценку уравнения регрессии:
Y = 34.66 + 1.97X1-2.45X2
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R2 = 1 - s2e/∑(yi - yср)2 = 1 - 33.18/77.2 = 0.57
F = R2/(1 - R2)*(n - m -1)/m = 0.57/(1 - 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы
k1 = 2 и k2 = n-m-1 = 5 - 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 < Fkp, то коэффициент детерминации статистически не значим, а следовательно, полученное уравнение регрессии статистически ненадежно. Это означает, что его нельзя использовать для прогноза и дальнейшего анализа.
Пример №2. Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X1 (%), а также по уровню инфляции X2 (%).
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| X1 | 3,5 | 2,8 | 6,3 | 4,5 | 3,1 | 1,5 | 7,6 | 6,7 | 4,2 | 2,7 | 4,5 | 3,5 | 5,0 | 2,3 | 2,8 |
| X2 | 4,5 | 3,0 | 3,1 | 3,8 | 3,8 | 1,1 | 2,3 | 3,6 | 7,5 | 8,0 | 3,9 | 4,7 | 6,1 | 6,9 | 3,5 |
| Y | 9,0 | 6,0 | 8,9 | 9,0 | 7,1 | 3,2 | 6,5 | 9,1 | 14,6 | 11,9 | 9,2 | 8,8 | 12,0 | 12,5 | 5,7 |
Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .

Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),

После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X1 + 1.4798X2
Скачать.
Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).
Пример №3.
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.
| ВВП | 16331,97 | 16763,35 | 17492,22 | 18473,83 | 19187,64 | 20066,25 | 21281,78 | 22326,86 | 23125,90 |
| Потребление в текущих ценах | 771,92 | 814,28 | 735,60 | 788,54 | 853,62 | 900,39 | 999,55 | 1076,37 | 1117,51 |
| Инвестиции в текущих ценах | 176,64 | 173,15 | 151,96 | 171,62 | 192,26 | 198,71 | 227,17 | 259,07 | 259,85 |
- Средние значения величин;
- Дисперсии величин;
- Среднеквадратические отклонения величин;
- Ковариацию ВВП и потребления, ковариацию ВВП и инвестиций;
- Коэффициент корреляции ВВП и потребления, ковариацию ВВП и инвестиций;
- Коэффициент частной корреляции ВВП и потребления, коэффициент частной корреляции ВВП и инвестиций;
- Построить уравнение регрессии для зависимости ВВП от потребления. Определить коэффициент детерминации и сделать вывод о качестве полученного уравнения регрессии. С помощью t-теста проверить гипотезу H0: β = 0 для пятипроцентного уровня значимости и сделать вывод о значимости полученного коэффициента. Построить девяностопятипроцентный доверительный интервал для коэффициента регрессии b. С помощью F-теста проверить полученное уравнение регрессии на значимость. Провести t-тест для коэффициента корреляции.
- Построить уравнение множественной регрессии для зависимости ВВП от потребления и инвестиций. Определить коэффициент детерминации и сделать вывод о качестве полученного уравнения регрессии. С помощью t-теста проверить гипотезы H0: β1 = 0, H0: β2 = 0 для пятипроцентного уровня значимости и сделать вывод о значимости полученных коэффициентов. Построить девяностопятипроцентный доверительный интервал для коэффициентов регрессии b1, b2. С помощью F-теста проверить полученное уравнение регрессии на значимость. Провести t-тест для коэффициента корреляции.
Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).
Пример №4. На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:
- Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
- Рассчитать частные коэффициенты эластичности. Сделать вывод.
- Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
- Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
- Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.
s = (XTX)-1XTY
Матрица X
| 1 | 3.9 | 10 |
| 1 | 3.9 | 14 |
| 1 | 3.7 | 15 |
| 1 | 4 | 16 |
| 1 | 3.8 | 17 |
| 1 | 4.8 | 19 |
| 1 | 5.4 | 19 |
| 1 | 4.4 | 20 |
| 1 | 5.3 | 20 |
| 1 | 6.8 | 20 |
| 1 | 6 | 21 |
| 1 | 6.4 | 22 |
| 1 | 6.8 | 22 |
| 1 | 7.2 | 25 |
| 1 | 8 | 28 |
| 1 | 8.2 | 29 |
| 1 | 8.1 | 30 |
| 1 | 8.5 | 31 |
| 1 | 9.6 | 32 |
| 1 | 9 | 36 |
Матрица Y
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 8 |
| 8 |
| 8 |
| 10 |
| 9 |
| 11 |
| 9 |
| 11 |
| 12 |
| 12 |
| 12 |
| 12 |
| 14 |
| 14 |
Матрица XT
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3.9 | 3.9 | 3.7 | 4 | 3.8 | 4.8 | 5.4 | 4.4 | 5.3 | 6.8 | 6 | 6.4 | 6.8 | 7.2 | 8 | 8.2 | 8.1 | 8.5 | 9.6 | 9 |
| 10 | 14 | 15 | 16 | 17 | 19 | 19 | 20 | 20 | 20 | 21 | 22 | 22 | 25 | 28 | 29 | 30 | 31 | 32 | 36 |
Умножаем матрицы, (XTY)
Находим определитель det(XTX)T = 139940.08
Находим обратную матрицу (XTX)-1

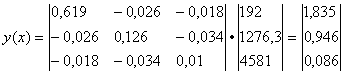
Y = 1.8353 + 0.9459X 1 + 0.0856X 2
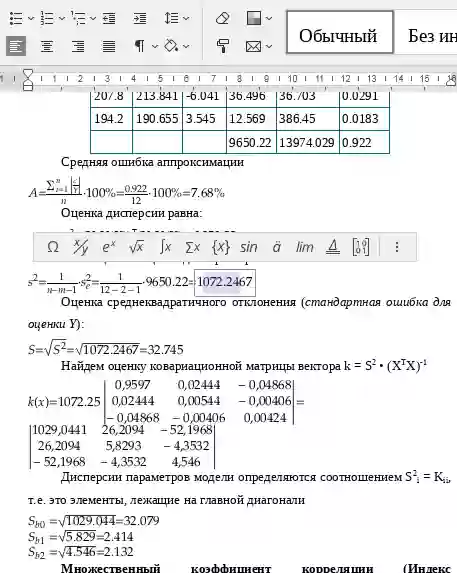
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y - X*s
| 0.62 |
| 0.28 |
| 0.38 |
| 0.01 |
| 0.11 |
| -1 |
| -0.57 |
| 0.29 |
| -0.56 |
| 0.02 |
| -0.31 |
| 1.23 |
| -1.15 |
| 0.21 |
| 0.2 |
| -0.07 |
| -0.07 |
| -0.53 |
| 0.34 |
| 0.57 |
se2 = (Y - X*s)T(Y - X*s)
Несмещенная оценка дисперсии равна
Оценка среднеквадратичного отклонения равна
Найдем оценку ковариационной матрицы вектора k = σ*(XTX)-1
| k(x) = 0.36 |
| = |
|
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)
Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора хi при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции - последовательно берутся пары yx1,yx2,... , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции
Коэффициент детерминации
R 2= 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл: Tтабл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл < Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - не значим
Проверка гипотез относительно коэффициентов уравнения регрессии
1) t-статистика
Tтабл (n-m-1;α/2) = (17;0.025) = 2.11
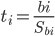
Находим стандартную ошибку коэффициента регрессии b0:
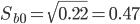
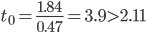
Статистическая значимость коэффициента регрессии b0 подтверждается.
Находим стандартную ошибку коэффициента регрессии b1:
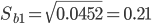
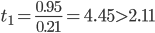
Статистическая значимость коэффициента регрессии b1 подтверждается.
Находим стандартную ошибку коэффициента регрессии b2: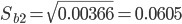
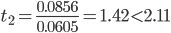
Статистическая значимость коэффициента регрессии b2 не подтверждается.
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(bi - ti Sbi; bi + ti Sbi)
b0: (1.84 - 2.11 • 0.47 ; 1.84 + 2.11 • 0.47) = (0.84;2.83)
b1: (0.95 - 2.11 • 0.21 ; 0.95 + 2.11 • 0.21) = (0.5;1.39)
b2: (0.0856 - 2.11 • 0.0605 ; 0.0856 + 2.11 • 0.0605) = (-0.042;0.21)
2) F-статистика. Критерий Фишера
Fkp = 3.2
Поскольку F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
Построение парной регрессионной модели
1) Рассчитайте корреляцию между, как минимум, тремя экономическими показателями из статистических данных по выборке не менее 15 наблюдений (из Интернета, печатных источников или Вашего предприятия). Интерпретируйте полученные данные.2) Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
3) Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели. Сравните адекватность модели с парной регрессией.
4) Проверьте любую из построенных моделей (парной или множественной регрессии) на отсутствие автокорреляции.
Рекомендации к решению контрольной работы.
Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.
Пример №3. Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x1, дохода компании x2 и объема инвестиций в расширение и модернизацию производства x3. Исходные данные представлены выборкой объема n=50.
Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x1, x2, x3 взятых по отдельности. Для каждой объясняющей переменной:
- Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
- Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации
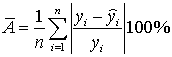 .
. - Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
- Постройте на поле корреляции прямую линию выборочной регрессии по точкам
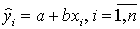 .
. - Постройте диаграмму остатков.
- Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение Fтабл определите с помощью функции FРАСПОБР).
- Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
- Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
- Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
- Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.
Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации 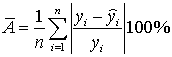 и дайте ей интерпретацию.
и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.