Временные ряды в эконометрических исследованиях

Большинство эконометрических моделей строится как динамические эконометрические модели. Это означает, что моделирование причинно-следственных связей между переменными осуществляется во времени, а исходные данные представлены в форме временных рядов.

Временной ряд х_t (t=1; n) – ряд значений какого-либо показателя за несколько последовательных промежутков времени.

Каждый временной ряд х_t складывается из следующих основных составляющих (компонентов):

Тенденции, характеризующей общее направление динамики изучаемого явления. Аналитически тенденция выражается некоторой функцией времени, называемой трендом (Т).
Циклической или периодической составляющей, характеризующей циклические или периодические колебания изучаемого явления. Колебания представляют собой отклонения фактических уровней ряда от тренда. Объем продаж некоторых товаров подвержен сезонным колебаниям. Сезонные колебания (S) – периодические колебания, которые имеют определенный и постоянный период равный годовому промежутку. Конъюнктурные колебания (К) связаны с большими экономическими циклами, период таких колебаний – несколько лет.
Случайной составляющей, которая является результатом воздействия множества случайных факторов (Е).

Тогда уровень ряда можно представить как функцию от этих составляющих (компонентов):

=f(T, K, S, E).

В зависимости от взаимосвязи между составляющими может быть построена либо аддитивная модель: =T+K+S+E, либо мультипликативная модель: =T·K·S·E ряда динамики.

Для определения состава компонентов (структуры временного ряда) в модели временного ряда строят автокорреляционную функцию.
Автокорреляция– корреляционная связь между последовательными уровнями одного и того же ряда динамики (сдвинутыми на определенный промежуток времени L - лаг). То есть, автокорреляция - это связь между рядом: x₁, x₂, ... x_n-l и рядом x_1+l, x_2+l, ...,x_n, где L- положительное целое число. Автокорреляция может быть измерена коэффициентом автокорреляции:
,
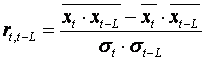где ,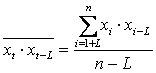
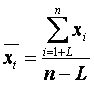– средний уровень ряда (x_1+L, x_2+L,...,x_n ),
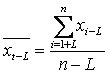средний уровень ряда (x₁, x₂,..., x_n-L ),
s_t, s_t-L – средние квадратические отклонения, для рядов (x_1+L, x_2+L,..., x_n ) и (x₁, x₂,..., x_n-L) соответственно.

Лаг (сдвиг во времени) определяет порядок коэффициента автокорреляции. Если L=1, то имеем коэффициент автокорреляции 1-ого порядка r_t,t-1, если L=2, то коэффициент автокорреляции 2-ого порядка r_t,t-₂и т.д. Следует учитывать, что с увеличением лага на единицу, число пар значений, по которым рассчитывается коэффициент автокорреляции уменьшается на 1. Поэтому обычно рекомендуют максимальный порядок коэффициента автокорреляции равный n/4.

Рассчитав несколько коэффициентов автокорреляции, можно определить лаг (L), при котором автокорреляция (r_t,t-L) наиболее высокая, выявив тем самым структуру временного ряда.

Если наиболее высоким оказывается значение коэффициента автокорреляции первого порядка r_t,t-₁, то исследуемый ряд содержит только тенденцию.
Если наиболее высоким оказался коэффициент автокорреляции r_t,t-L порядка L, то ряд содержит колебания периодом L.
Если ни один из r_t,t-L не является значимым, можно сделать одно из двух предположений:
- либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
- либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.

Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции) называют коррелограммой.

Для выявления закономерных колебаний внутри года при выполнении контрольной работы рекомендуется рассчитывать не меньше 4-х уровней коэффициентов автокорреляции.
Рассмотрим на примере как построить коррелограмму, чтобы определяется структуру временного ряда.
Пусть нам даны поквартальные данные об объеме выпуска некоторого товара некоторой фирмой –х (усл.ед.) за 3 года:

1993				1994				1995
1	2	3	4	1	2	3	4	1	2	3	4
410	560	715	500	520	740	975	670	705	950	1200	900

Чтобы построить коррелогорамму для нашего примера, исходный ряд динамики дополним рядами из уровней этого ряда, сдвинутыми во времени (таблица 6).
Таблица 6

t	1	2	3	4	5	6	7	8	9	10	11	12
х_t	-	560	715	500	520	740	975	670	705	950	1200	900	r_t,t-1=0,537
x_t-1	-	410	560	715	500	520	740	975	670	705	950	1200	r_t,t-1=0,537
х_t	-	-	715	500	520	740	975	670	705	950	1200	900	r_t,t-2=0,085
х_t-2	-	-	410	560	715	500	520	740	975	670	705	950	r_t,t-2=0,085
х_t	-	-	-	500	520	740	975	670	705	950	1200	900	r_t,t-3=0,445
х_t-3	-	-	-	410	560	715	500	520	740	975	670	705	r_t,t-3=0,445
х_t	-	-	-	-	520	740	975	670	705	950	1200	900	r_t,t-4=0,990
х_t-4	-	-	-	-	410	560	715	500	520	740	975	670	r_t,t-4=0,990
х_t	-	-	-	-	-	740	975	670	705	950	1200	900	r_t,t-5=0,294
х_t-5	-	-	-	-	-	410	560	715	500	520	740	975	r_t,t-5=0,294

Рассчитаем коэффициенты корреляции:
1-ого порядка для рядов х_t и х_{t -1} ,
2-ого порядка для рядов х_t и х_{t -2} ,
3-его порядка для рядов х_t и х_{t -3} ,
4-ого порядка для рядов х_t и х_{t -4,}
5-ого порядка для рядов х_t и х_{t -5}

Результаты расчетов представлены в таблице 7.
Таблица 7

Лаг (порядок) – L	r_t,t-L	Коррелограмма
1	0,537	****
2	0,085	*
3	0,445	***
4	0,990	*****
5	0,294	**

Вывод: в данном ряду динамики имеется тенденция (т.к. r_t,t-1=0,537 →1) и периодические колебания с периодом (L) равным 4, т.е. имеют место сезонные колебания (т.к. r_t,t-4=0,99 →1).

Построение модели временного ряда с сезонными колебаниями (аддитивная модель).
Процесс построения модели временного ряда (х), содержащего n уровней некоторого показателя за Z лет, с L сезонными колебаниями включает следующие шаги:
1) Выравнивание исходного ряда методом скользящей средней (х^c ). Произведем выравнивание исходного ряда взятого из примера, рассмотренного выше, методом скользящей средней с периодом усреднения равным 3. Результаты представлены в таблице 9 (столбец 4).
2) Расчет значений сезонной составляющейS_i, i=1;L , где L– число сезонов в году. Для нашего примера L=4 (сезоны - кварталы).
Расчет значений сезонных составляющих осуществляется после устранения тенденции из исходных уровней ряда: x-x^c (столбец 5, таблица 9). Для дальнейшего расчета S_i построим отдельную таблицу. Строки данной таблицы соответствуют сезонам, столбцы - годам. В теле таблицы находятся значения: x -x^c . По этим данным рассчитываются средние оценки сезонных составляющих каждой строке (S^c_i). Если сумма всех средних оценок равна нулю ( ), то данные средние и будут окончательными значениями сезонных составляющих (S_i=S^c_i). Если их сумма не равна нулю, то рассчитываются скорректированные значения сезонных составляющих вычитанием из средней оценки величины равной отношению суммы средних оценок к их общему числу (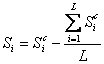). Для нашего примера расчет значений S_i представлен в таблице 8.
Таблица 8

Номер сезона	Год 1	Год 2	Год 3	Средняя оценка сезонной составляющей	Скорректированная оценка сезонной составляющей S_i
1	-	-66,67	-70,00	-68,33	-67,15
2	-1,67	-5,00	-1,67	-2,78	-1,60
3	123,33	180 ,00	183,33	162,22	163,40
4	-78,33	-113,33	-	-95,83	-94,66
Итого				-4, 72	0

3) Устранение влияния сезонной составляющей из исходного ряда динамики: x^S = x-S_i . Результаты расчета x^S для нашего примера представлены в столбце 6 таблицы 9.
4) Аналитическое выравнивание уровней x^S (построение тренда):

.
Расчет параметров при аналитическом выравнивании чаще всего производится с помощью метода наименьших квадратов (МНК). При этом поиск параметров для линейного уравнения тренда можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю. Для этого вводится новая условная переменная времени t^y, такая, что åt^y =0. Уравнение тренда при этом будет следующим:

.
При нечетном числе уровней ряда динамики для получения å t^y=0 уровень, находящийся в середине ряда, принимается за условное начало отсчета времени (периоду или моменту времени, соответствующему данному уровню присваивается нулевое значение). Даты времени, расположенные левее этого уровня, обозначаются натуральными числами со знаком минус (-1 –2 –3 ...), а даты времени, расположенные правее этого уровня – натуральными числами со знаком плюс (1 2 3 ...).
Если число уровней ряда четное, периоды времени левой половины ряда (до середины) нумеруются –1, -3, -5 и т.д. А периоды правой половины - +1, +3, +5 и.т.д. При этом åt^y будет равна 0.
Система нормальных уравнений (соответствующих МНК) преобразуется к виду:

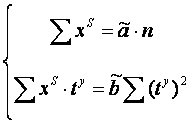
Отсюда параметры уравнения рассчитываются по формулам:

.
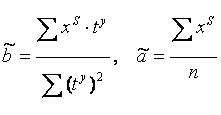Интерпретация параметров линейного уравнения тренда

- уровень ряда за период времени t^у =0;

- средний абсолютный прирост уровня ряда за единичный промежуток времени.
В нашем примере четное число уровней ряда: n=12. Следовательно, условная переменная времени для 6-ого элемента ряда будет равна –1, а для 7-ого +1. Значения переменной _i^y содержатся во 2-ом столбце таблицы 9.
Параметры линейного тренда будут:

=14257,5/572=24,93;

=8845/12=737,08. Это значит, что с каждым кварталом объем выпуска товара в среднем увеличивается на 2∙28,7 усл.ед. А средний за период с 1993 по 1995гг объем выпуска составил 738,75 усл.ед.
Рассчитаем значения трендовой компоненты по формуле

(столбец 7 таблицы 9).
5) Учет сезонной составляющей в выровненных уровнях ряда (

=T+S). Результаты расчета для нашего примера представлены в столбце 8 таблицы 9.
6) Расчет абсолютной ошибки временного ряда (Е= x-

) осуществляется для оценки качества полученной модели. Результаты расчета для нашего примера представлены в столбце 9 таблицы 9.
Таблица 9

T	t^у	x	x^c	x-x^c	x^s	T		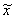E
1	2	3	4	5	6	7	8	9
1	-11	410	-	-	477,15	462,9 0	395,75	14,25
2	-9	560	561,67	-1,67	561,60	512,75	511,15	48,85
3	-7	715	591,67	123,33	551,60	562,60	726,00	-11,01
4	-5	500	578,33	-78,33	594,65	612,45	517,80	-17,80
5	-3	520	586,67	-66,67	587,15	662,31	595,15	-75,15
6	-1	740	745 ,00	-5 ,00	741,60	712,16	710,56	29,44
7	1	975	795 ,00	180 ,00	811,60	762,00	925,41	49,59
8	3	670	783,33	-113,33	764,65	811,86	717,21	-47,21
9	5	705	775 ,00	-70 ,00	772,15	861,71	794,56	-89,56
10	7	950	951,67	-1,67	951,60	911,56	909,97	40,03
11	9	1200	1016,67	183,33	1036, 60	961,41	1124,82	75,18
12	11	900	-	-	994,65	1011,27	916,61	-16,61
Итого	8845			8845,00	8845,00	8845,00	16,61

Значимость параметров линейного уравнения тренда (Т) определяется на основе t -критерия Стьюдента также как и в линейном парном регрессионном анализе.

Прогнозирование по аддитивной модели.
Пусть требуется дать прогноз уровня временного ряда на период (n +1). Точечный прогноз значения уровня временного ряда х_n+1 в аддитивной модели есть сумма трендовой компоненты и сезонной компоненты (соответствующей i –ому сезону прогноза): =T_n+1+S_i.
Для построения доверительного интервала прогноза нужно рассчитать среднюю ошибку прогноза:
m^р = ,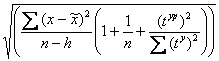
где h- число параметров в уравнении тренда;
t^yp – значение условной переменной времени для периода прогнозирования.
Затем рассчитаем предельную ошибку прогноза: D^р =t_a · m_р,
где t_a- коэффициент доверия, определяемый по таблицам Стьюдента по уровню значимости α и числу степеней свободы равным (n-h).
Окончательно получим: (-D^р; +D^р).

Временные ряды в эконометрических исследованиях

Правила ввода данных

Поиск

Процесс

Сообщение