Оптимизация сетевого графика методом «время – стоимость»
При использовании этого метода предполагают, что при уменьшении продолжительности работы возрастает ее стоимость.Продолжительность работы t(i, j) может находиться в пределах a(i,j)≤t(i,j)≤b(i,j), где a(i,j) – минимально возможная (экстренная) продолжительность работы (i, j), которую только можно осуществить в условиях разработки; b(i, j) – нормальная продолжительность выполнения работы. При этом стоимость c(i, j) работы (i, j) заключена в пределах cmin(i, j) (при нормальной продолжительности работы) до cmax(i, j) (при экстренной продолжительности работы).
Из соображений удобства принимается, что зависимость величины c от t является линейной, т. е. график функции c = c(t) имеет следующий вид (рис. 1).
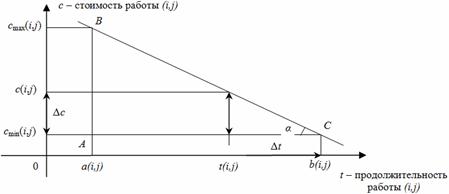
Рис. 1
Выясним, на сколько возрастут затраты c(i, j), если продолжительность работы уменьшить с величины b(i, j) до t(i, j). Обозначим через α угол наклона прямой (острый угол между прямой и осью t), пусть tg α=h(i,h). Тогда прирост стоимости
Δc=c(i,j)-cmin(i,j)=Δ·tg α, т. е. Δc=[b(i,j)-t(i,j)]·h(i,j), (1)
Величина h(i,j) показывает затраты на ускорение работы(i, j) на единицу времени (по сравнению с нормальной продолжительностью). Из треугольника ABC
![]() (2)
(2)
Пример. Оптимизировать сетевой график. Исходные данные представлены в таблице (1).
| Работа (i, j) | Продолжительность работы, сутки | Коэффициент затрат на ускорение работы h(i, j) | Стоимость работы, усл. руб. c(i, j) при t= b(i, j) | |
| минимальная a(i, j) | максимальная b(i, j) | |||
| (0,1) | 10 | 20 | 6 | 35 |
| (0,2) | 12 | 32 | 3 | 50 |
| (1,2) | 2 | 12 | 3 | 15 |
| (1,3) | 2 | 7 | 8 | 10 |
| (2,7) | 2 | 7 | 3 | 10 |
| (3,4) | 16 | 26 | 2 | 50 |
| (3,5) | 8 | 13 | 6 | 15 |
| (4,6) | 12 | 22 | 4 | 40 |
| (5,6) | 20 | 25 | 4 | 30 |
| (6,7) | 8 | 13 | 5 | 25 |
| (7,8) | 6 | 11 | 9 | 20 |
| Итого | 300 | |||
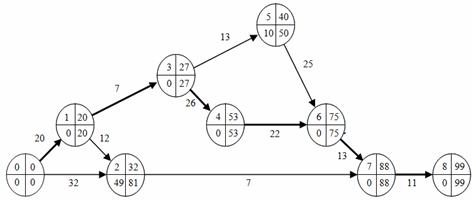
Критические работы (0,1), (1,3), (3,4), (4,6), (6,7), (7,9) на рисунке выделены жирными стрелками. Продолжительность критического пути Tкр = 99 суток.
I шаг. Рассмотрим коэффициенты затрат критических работ. Из таблицы:
h(0, 1) = 6, h(1, 3) = 8, h(3, 4) = 2, h(4, 6) = 4, h(6, 7) = 5, h(7, 8) = 9.
Наименьший коэффициент на ускорение имеет работа (3, 4), поэтому прежде всего будем сокращать ее продолжительность. Поскольку максимальная продолжительность b(3,4)=26, а минимальная – a(3,4), продолжительность работы (3,4) можно сократить максимум на 10 суток, при этом по формуле (6.22) стоимость проекта возрастет на величину Δc=10·2=20 (усл. руб.) и составит 300+20=320 (усл. руб.).
Длина критического пути уменьшится максимум на 10 суток (с 99 до 89).
Найдем другие полные пути, не совпадающие с критическим:
L2: 0 → 1 → 3 → 5 → 6 → 7 → 8;
L3: 0 → 1 → 2 → 7 → 8;
L4: 0 → 2 → 7 → 8,
их продолжительности:
t(L2)=20+7+13+25+13+11=89;
t(L3)=20+12+7+11=50;
t(L4)=32+7+11=50;
II шаг. Теперь у нас два критических пути: L1 и L2, и сократить срок выполнения проекта можно за счет одновременного сокращения их продолжительности. Это можно сделать, уменьшив продолжительности работ, лежащих на этих путях (0, 1), (1, 3) (6, 7) или (7, 8).
Затраты на ускорение этих работ: h(0, 1) = 6, h(1, 3) = 8, h(6, 7) = 5, h(7, 8) = 9.
Минимальный из этих коэффициентов 5, поэтому будем сокращать t(6, 7). ее можно сократить максимум на 13 – 8 = 5 суток.
На эту величину уменьшатся длины критических путей и срок выполнения проекта. При этом стоимость увеличится на 5 · 5 = 25 усл. руб. и составит 320 + 25 = 345 руб.
Теперь t(L1)=t(L2)=84, t(L3)=t(L4)=50.
III шаг. Выбираем минимальное из чисел:
h(0, 1) = 6, h(1, 3) = 8, h(7, 8) = 9, это h(0, 1) = 6. Работу (0, 1) сокращаем на 20 – 10 = 10 суток, стоимость возрастет на 6·10 = 60 усл. руб. и составит 345 + 60 = 405 усл. руб.
Теперь t(L1)=t(L2)=74, t(L3)=50-10=40, t(L4)=50.
IV шаг. Минимальное из чисел h(1, 3) = 8, h(7, 8) = 9 есть h(1, 3) = 8. Сокращаем продолжительность (1, 3) на 7 – 2 = 5 суток, стоимость возрастет на 8 · 5 = 40 усл. руб. и составит 405 + 40 = 445 усл. руб.
t(L1)=t(L2)=69, t(L3)=40, t(L4)=50.
V шаг. Сокращаем продолжительность работы (7, 8) на 11 – 6 = 5 суток, стоимость возрастет на 9 · 5 = 45 усл. руб. и составит c = 445 + 45 = 490 руб.
t(L1)=t(L2)=64, t(L3)=40, t(L4)=50.
VI шаг. На L1 осталась несокращенной работа (4, 6), на L2 – работы (3, 5) и (5, 6). Если сократить одну из них, то срок выполнения проекта не изменится. Поэтому сократим одну работу на L1, одну – на L2 на одно и то же количество суток. Так как 22 – 12 = 10, 13 – 8 = 5, 25 – 20 = 5, то сокращаем работы (4, 6) и (5, 6) на 5 суток (коэффициент h(5, 6) = 4, h(3, 5) = 6). Стоимость возрастет на 4 · 5 + 4 · 5 = 40 руб. и составит 490 + 40 = 530 усл. руб.
t(L1)=t(L2)=59, t(L3)=35, t(L4)=45.
VII шаг. Можно сократить работу (4, 6) еще на 5 суток и работу (3, 5) тоже на 5 суток, тогда стоимость возрастет на 4 · 5 + 6 · 5 = 50 усл. руб. и составит 530 + 50 = 580 усл. руб.; срок t(L1)=t(L2)=54 суток.
График функции c(t) имеет следующий вид (рис. 3).
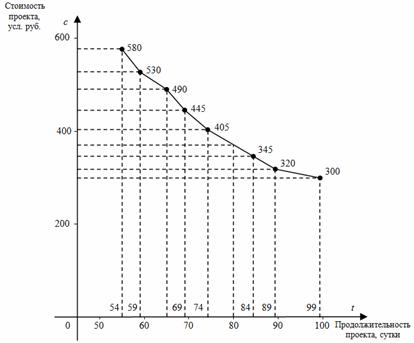
Рис. 3
С помощью этого графика можно:
1) оценить стоимость проекта при любом возможном сроке его выполнения. Например, найдем стоимость проекта для срока t = 80 суток. Запишем уравнение прямой, проходящей через две точки (74, 405) и (84, 345):
![]() ;
; ![]() ;
; ![]() .
.
Подставляя в формулу c=849-6t время t = 80, найдем с(80) = 849 – 6 · 80 = 369 (усл. руб.);
2) найти продолжительность выполнения проекта при заданной стоимости. Например, определим продолжительность для c = 540 руб. Уравнение прямой через точки (54, 580) и (59, 530):
![]() ;
; ![]() ;
;
-10(t-54)=c-580; 10t+540=c-580.
При с = 540 найдем t= 58 суток.

