Двойственный симплексный метод
Двойственный симплексный метод основан на теории двойственности (см. решение двойственной задачи) и используется для решения задач линейного программирования, свободные члены которых bi могут принимать любые значения, а система ограничений задана неравенствами смысла «≤», «≥» или равенством «=».Назначение сервиса. Онлайн-калькулятор используется для решения задач линейного программирования P-методом в следующих формах записи: базовой форме записи симплекс-метода, в виде симплексной таблицы, модифицированным симплекс-методом.
Графический метод решения ЗЛП
Решение транспортной задачи
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X)зависит от количества реализованных партий товара Х и представлен в таблице.
| Объем товара Х (в партиях) | Доход G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
В P-методе оптимальный план получается в результате движения по псевдопланам. Псевдоплан - план, в котором условия оптимальности удовлетворяются, а среди значений базисных переменных xi имеются отрицательные числа. Алгоритм двойственного симплекс-метода включает следующие этапы:
- Составление псевдоплана. Систему ограничений исходной задачи приводят к системе неравенств смысла «≤».
- Проверка плана на оптимальность. Если в полученном опорном плане не выполняется условие оптимальности, то задача решается симплексным методом.
- Выбор ведущих строки и столбца. Среди отрицательных значений базисных переменных выбираются наибольшие по абсолютной величине. Строка, соответствующая этому значению, является ведущей.
- Расчет нового опорного плана. Новый план получается в результате пересчета симплексной таблицы методом Жордана-Гаусса. Далее переход к этапу 2.
Алгоритм двойственного симплекс-метода
1) выбирают разрешающую строку по наибольшему по абсолютной величине отрицательному элементу столбца свободных членов;
2) выбирают разрешающий столбец по наименьшему по абсолютной величине отношению элементов L строки к отрицательным элементам разрешающей строки;
3) пересчитывают симплексную таблицу по правилам обычного симплекс-метода;
4) решение проверяют на оптимальность. Признаком получения допустимого оптимального решения является отсутствие в столбце свободных членов отрицательных элементов.
Замечания
1. Если в разрешающей строке нет ни одного отрицательного элемента, задача неразрешима.
2. Если ограничения задачи заданы неравенствами типа «≥», двойственный симплекс-метод позволяет избавиться от необходимости введения искусственных переменных.
Особенности двойственного симплекс-метода Используются при решении методом Гомори.
Пример №1. Решить задачу, используя алгоритм двойственного симплекс-метода
L = x1 + 4x2 → min
2х1+3х2+4х3 ≥ 20
5х1-х2+2х3 ≥ 12
х1+2х2-х3 ≤ 2
х1+4х2-2х3 ≤ 1
х1, х2, х3 ≥ 0
Составляем исходную симплексную таблицу.
| Баз. | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Св. |
| x4 | -2 | -3 | -4 | 1 | 0 | 0 | 0 | -20 |
| x5 | -5 | 1 | -2 | 0 | 1 | 0 | 0 | -12 |
| x6 | 1 | 2 | -1 | 0 | 0 | 1 | 0 | 2 |
| x7 | -1 | 4 | -2 | 0 | 0 | 0 | 1 | 1 |
| L | -1 | -4 | -1 | 0 | 0 | 0 | 0 | 0 |
Отсутствие в L строке положительных оценок свидетельствует об оптимальности исходного решения, а наличие в столбце свободных членов отрицательных элементов – о его недопустимости. Согласно алгоритму двойственного симплекс-метода выбираем разрешающую строку по наибольшему по абсолютной величине отрицательному элементу столбца свободных элементов. В нашем примере разрешающая строка – первая. Разрешающий столбец выбирается в соответствии с правилом, изложенным в пункте 2 схемы алгоритма. Разрешающий элемент равен (-4). После пересчета получаем следующую таблицу
| Баз. | х1 | х2 | х3 | х4 | х5 | х6 | х7 | Св. |
| х3 | 1/2 | 3/4 | 1 | -1/4 | 0 | 0 | 0 | 5 |
| х5 | -4 | 5/2 | 0 | -1/2 | 1 | 0 | 0 | -2 |
| х6 | 3/2 | 11/4 | 0 | -1/4 | 0 | 1 | 0 | 7 |
| х7 | 0 | 11/2 | 0 | -1/2 | 0 | 0 | 1 | 11 |
| L | -1/2 | -13/4 | 0 | -1/4 | 0 | 0 | 0 | 5 |
Аналогично рассуждая, получим еще одну таблицу
| Баз. | х1 | х2 | х3 | х4 | х5 | х6 | х7 | Св. |
| х3 | 0 | 17/16 | 1 | -5/16 | 1/8 | 0 | 0 | 19/4 |
| х1 | 1 | -5/8 | 0 | 1/8 | -1/4 | 0 | 0 | 1/2 |
| х6 | 0 | 59/16 | 0 | -7/16 | 3/8 | 1 | 0 | 25/4 |
| х7 | 0 | 11/2 | 0 | -1/2 | 0 | 0 | 1 | 11 |
| L | 0 | -57/16 | 0 | -3/16 | -1/8 | 0 | 0 | 21/4 |
Отсутствие в столбце свободных членов отрицательных элементов свидетельствует о том, что получено оптимальное решение Lmin=21/4, Xmin(1/2; 0; 19/4; 0; 25/4; 11).
Замечание. Если решение ЗЛП и недопустимо и неоптимально, то сначала получаем допустимое решение, используя алгоритм двойственного симплекс-метода, а затем по правилам обычного симплекс-метода получаем оптимальное решение.
Пример.
L = 5x1 – x2 – x3 → max
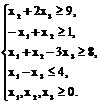 или
или 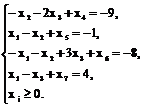
Составляем исходную симплекс-таблицу
| Баз. | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Св. |
| x4 | 0 | -1 | -2 | 1 | 0 | 0 | 0 | -9 |
| x5 | 1 | -1 | 0 | 0 | 1 | 0 | 0 | -1 |
| x6 | -1 | -1 | 3 | 0 | 0 | 1 | 0 | -8 |
| x7 | 1 | 0 | -1 | 0 | 0 | 0 | 1 | 4 |
| L | -5 | 1 | 4 | 0 | 0 | 0 | 0 | 0 |
Решение недопустимо, так как в столбце свободных членов есть отрицательные элементы и неоптимально, так как в строке L есть отрицательная оценка (-5). Получаем сначала допустимое решение, используя алгоритм двойственного симплекс-метода. После пересчета получаем следующую симплексную таблицу
| Баз. | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Св. |
| x2 | 0 | 1 | 2 | -1 | 0 | 0 | 0 | 9 |
| x5 | 1 | 0 | 2 | -1 | 1 | 0 | 0 | 8 |
| x6 | -1 | 0 | 5 | -1 | 0 | 1 | 0 | 1 |
| x7 | -1 | 0 | -1 | 0 | 0 | 0 | 1 | 4 |
| L | -5 | 0 | 2 | 1 | 0 | 0 | 0 | -9 |
Используем обычный симплекс-метод и получаем следующие таблицы
| Баз. | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Св. |
| x2 | 0 | 1 | 2 | -1 | 0 | 0 | 0 | 9 |
| х5 | 0 | 0 | 3 | -1 | 1 | 0 | -1 | 4 |
| х6 | 0 | 0 | -4 | -1 | 0 | 1 | 1 | 5 |
| x1 | 1 | 0 | -1 | 0 | 0 | 0 | 1 | 4 |
| L | 0 | 0 | -3 | 1 | 0 | 0 | 5 | 11 |
| Баз. | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Св. |
| x2 | 0 | 1 | 0 | -1/2 | 0 | -1/2 | -1/2 | 13/2 |
| x5 | 1 | 0 | 0 | -1/4 | 1 | -3/4 | -7/4 | 1/4 |
| x6 | 0 | 0 | 1 | -1/4 | 0 | 1/4 | 1/4 | 5/4 |
| x1 | 0 | 0 | 0 | -1/4 | 0 | 1/4 | 5/4 | 21/4 |
| L | 0 | 0 | 0 | 1/4 | 0 | 3/4 | 23/4 | 59/4 |
Отсутствие в строке L отрицательных оценок свидетельствует о том, что получено оптимальное решение.
Lmax=59/4, Xmax(21/4; 13/2; 5/4; 0; 1/4; 0; 0).
Пример. Предприятию необходимо выпустить по плану продукции А1 единиц, А2 единиц, А3 единиц. Каждый вид изделия может производиться на двух машинах.
Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальны? Дана матрица затрат и ресурс времени каждой машины. Записать модель исследуемой операции в форме, допускающей использование P–метода.
Известно, что содержание n питательных веществ A, B и С в рационе должно быть не менее m1, m2, m3 единиц соответственно. Указанные питательные вещества содержат три вида продуктов. Содержание единиц питательных веществ в одном килограмме каждого из видов продукта приведено в таблице. определите дневной рацион, обеспечивающий получение необходимого количества питательных веществ при минимальных денежных затратах.
Задание: Решить задачу, используя алгоритм двойственного симплекс-метода.
Приведем систему ограничений к системе неравенств смысла ≤, умножив соответствующие строки на (-1).
Определим минимальное значение целевой функции F(X) = 4x1 + 2x2 + x3 при следующих условиях-ограничений.
- x1 - x2≤-10
2x1 + x2 - x3≤8
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В первом неравенстве смысла (≤) вводим базисную переменную x4. Во втором неравенстве смысла (≤) вводим базисную переменную x5.
-1x1-1x2 + 0x3 + 1x4 + 0x5 = -10
2x1 + 1x2-1x3 + 0x4 + 1x5 = 8
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| A = |
|
x4, x5,
Полагая, что свободные переменные равны нулю, получим первый опорный план:
X1 = (0,0,0,-10,8)
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x4 | -10 | -1 | -1 | 0 | 1 | 0 |
| x5 | 8 | 2 | 1 | -1 | 0 | 1 |
| F(X0) | 0 | -4 | -2 | -1 | 0 | 0 |
Итерация №1
1. Проверка критерия оптимальности.
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
2. Определение новой свободной переменной.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет первая строка, а переменную x4 следует вывести из базиса.
3. Определение новой базисной переменной. Минимальное значение θ соответствует 2-му столбцу, т.е. переменную x2 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-1).
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x4 | -10 | -1 | -1 | 0 | 1 | 0 |
| x5 | 8 | 2 | 1 | -1 | 0 | 1 |
| F(X0) | 0 | -4 | -2 | -1 | 0 | 0 |
| θ | 0 | -4 : (-1) = 4 | -2 : (-1) = 2 | - | - | - |
4. Пересчет симплекс-таблицы. Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 10 | 1 | 1 | 0 | -1 | 0 |
| x5 | -2 | 1 | 0 | -1 | 1 | 1 |
| F(X0) | 20 | -2 | 0 | -1 | -2 | 0 |
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 | x 5 |
| -10 : -1 | -1 : -1 | -1 : -1 | 0 : -1 | 1 : -1 | 0 : -1 |
| 8-(-10 • 1):-1 | 2-(-1 • 1):-1 | 1-(-1 • 1):-1 | -1-(0 • 1):-1 | 0-(1 • 1):-1 | 1-(0 • 1):-1 |
| 0-(-10 • -2):-1 | -4-(-1 • -2):-1 | -2-(-1 • -2):-1 | -1-(0 • -2):-1 | 0-(1 • -2):-1 | 0-(0 • -2):-1 |
Итерация №2
1. Проверка критерия оптимальности.
План 1 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
2. Определение новой свободной переменной.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет вторая строка, а переменную x5 следует вывести из базиса.
3. Определение новой базисной переменной. Минимальное значение θ соответствует третьему столбцу, т.е. переменную x3 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-1).
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 10 | 1 | 1 | 0 | -1 | 0 |
| x5 | -2 | 1 | 0 | -1 | 1 | 1 |
| F(X0) | 20 | -2 | 0 | -1 | -2 | 0 |
| θ | 0 | - | - | -1 : (-1) = 1 | - | - |
4. Пересчет симплекс-таблицы. Выполняем преобразования.
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 10 | 1 | 1 | 0 | -1 | 0 |
| x3 | 2 | -1 | 0 | 1 | -1 | -1 |
| F(X1) | 22 | -3 | 0 | 0 | -3 | -1 |
| B | x 1 | x 2 | x 3 | x 4 | x 5 |
| 10-(-2 • 0):-1 | 1-(1 • 0):-1 | 1-(0 • 0):-1 | 0-(-1 • 0):-1 | -1-(1 • 0):-1 | 0-(1 • 0):-1 |
| -2 : -1 | 1 : -1 | 0 : -1 | -1 : -1 | 1 : -1 | 1 : -1 |
| 20-(-2 • -1):-1 | -2-(1 • -1):-1 | 0-(0 • -1):-1 | -1-(-1 • -1):-1 | -2-(1 • -1):-1 | 0-(1 • -1):-1 |
В базисном столбце все элементы положительные. Переходим к основному алгоритму симплекс-метода.
Итерация №3
1. Проверка критерия оптимальности.
Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи.
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 10 | 1 | 1 | 0 | -1 | 0 |
| x3 | 2 | -1 | 0 | 1 | -1 | -1 |
| F(X1) | 22 | -3 | 0 | 0 | -3 | -1 |
Оптимальный план можно записать так: x1 = 0, x2 = 10, x3 = 2
F(X) = 2•10 + 1•2 = 22
Пример №2. Задание.
5x1 + 6x2≥1
15x1≥1
7x1 + 12x2≥1
Приведем систему ограничений к системе неравенств смысла ≤, умножив соответствующие строки на (-1).
Определим минимальное значение целевой функции F(X) = x1 + x2 при следующих условиях-ограничений.
- 5x1 - 6x2≤-1
- 15x1≤-1
- 7x1 - 12x2≤-1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x3. В 2-м неравенстве смысла (≤) вводим базисную переменную x4. В 3-м неравенстве смысла (≤) вводим базисную переменную x5.
-5x1-6x2 + 1x3 + 0x4 + 0x5 = -1
-15x1 + 0x2 + 0x3 + 1x4 + 0x5 = -1
-7x1-12x2 + 0x3 + 0x4 + 1x5 = -1
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| A= | -5 | -6 | 1 | 0 | 0 |
| -15 | 0 | 0 | 1 | 0 | |
| -7 | -12 | 0 | 0 | 1 |
Решим систему уравнений относительно базисных переменных:
x3, x4, x5,
Полагая, что свободные переменныеравны 0, получим первый опорный план:
X1 = (0,0,-1,-1,-1)
Базисное решениеназывается допустимым, если оно неотрицательно.
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x3 | -1 | -5 | -6 | 1 | 0 | 0 |
| x4 | -1 | -15 | 0 | 0 | 1 | 0 |
| x5 | -1 | -7 | -12 | 0 | 0 | 1 |
| F(X0) | 0 | -1 | -1 | 0 | 0 | 0 |
Пример решения Р-методом
Условие задачи. Предприятию необходимо выпустить по плану продукции А1– 500 единиц, А2– 300 единиц, А3– 450 единиц. Каждый вид изделия может производиться на двух машинах.Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальны? Дана матрица затрат и ресурс времени каждой машины. Записать модель исследуемой операции в форме, допускающей использование P – метода.
| Матрица затрат времени на производство видов продукции g – го вида A=(aig) | ||||
| Машины | Виды продукции | Ресурс времени машин | ||
|
А1 | А2 |
А3 | ||
| 1 | 2 | 3 | 3 | 1500 |
|
2 | 5 |
4 | 1 |
1000 |
| План выпуска продукции | 500 | 300 | 450 | |
Составим математическую модель задачи.
2x11+ 3x12+3x13≤ 1500
5x21+ 4x22+x23≤ 1000
x11+ x21≥ 500
x12+ x22≥ 300
x13+ x23≥ 450
Целевая функция:
2x11+ 3x12+3x13+ 5x21+ 4x22+x23→ min
Запишем в виде, решаемом Р-методом.
2x11+ 3x12+3x13≤ 1500
5x21+ 4x22+x23≤ 1000
-x11 -x21≤ -500
-x12-x22≤ -300
-x13-x23≤ -450
Определим минимальное значение целевой функции F(X) = 2x1+3x2+3x3+5x4+4x5+x6при следующих условиях-ограничений.
2x1+3x2+3x3≤1500
5x4+4x5+x6≤1000
-x1-x4≤-500
-x2-x5≤-300
-x3-x6≤-450
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
2x1+ 3x2+ 3x3+ 0x4+ 0x5+ 0x6+ 1x7+ 0x8+ 0x9+ 0x10+ 0x11= 1500
0x1+ 0x2+ 0x3+ 5x4+ 4x5+ 1x6+ 0x7+ 1x8+ 0x9+ 0x10+ 0x11= 1000
-1x1+ 0x2+ 0x3-1x4+ 0x5+ 0x6+ 0x7+ 0x8+ 1x9+ 0x10+ 0x11= -500
0x1-1x2+ 0x3+ 0x4-1x5+ 0x6+ 0x7+ 0x8+ 0x9+ 1x10+ 0x11= -300
0x1+ 0x2-1x3+ 0x4+ 0x5-1x6+ 0x7+ 0x8+ 0x9+ 0x10+ 1x11= -450
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| 2 | 3 | 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
|
0 | 0 |
0 | 5 |
4 | 1 |
0 | 1 |
0 | 0 |
0 |
| -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
|
0 | -1 |
0 | 0 |
-1 | 0 |
0 | 0 |
0 | 1 |
0 |
| 0 | 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 |
Решим систему уравнений относительно базисных переменных:
x7, x8, x9, x10, x11,
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,0,0,0,0,1500,1000,-500,-300,-450)
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
| 0 |
x7 | 1500 |
2 | 3 |
3 | 0 |
0 | 0 |
1 | 0 |
0 | 0 |
0 |
| | x8 | 1000 | 0 | 0 | 0 | 5 | 4 | 1 | 0 | 1 | 0 | 0 | 0 |
| |
x9 | -500 |
-1 | 0 |
0 | -1 |
0 | 0 |
0 | 0 |
1 | 0 |
0 |
| | x10 | -300 | 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | 0 |
| |
x11 | -450 |
0 | 0 |
-1 | 0 |
0 | -1 |
0 | 0 |
0 | 0 |
1 |
| Индексная строка | F(X0) | 0 | -2 | -3 | -3 | -5 | -4 | -1 | 0 | 0 | 0 | 0 | 0 |
| θ |
| |
2 | |
| 5 |
| |
| |
| |
|
Оптимальный план можно записать так: x5 = 133.33, x8 = 16.67, x1 = 500, x2 = 166.67, x6 = 450
F(X) = 2*500 + 3*166.67 + 4*133.33 + 1*450 = 2483.33
Пример №1. Предприятию необходимо выпустить по плану продукции, не менее, чем: А 1 - 500 единиц, А2 – 300 единиц, А 3 – 450 единиц. Каждый вид изделия может производиться на двух машинах. Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальными, если задана матрица затрат. Ресурс времени каждой машины приведен справа от таблицы. Записать модель исследуемой операции в форме, допускающей использование Р-метода. Решить задачу Р-методом.
Пример №2. Из 4 видов кормов необходимо составить рацион, в состав которого должно входить не менее в1 ед. вещества А, в 2 ед. вещества В и в 3 ед. вещества С. Количество единиц вещества, содержащегося в 1 кг корма каждого вида, указано в соответствующей таблице. В ней же приведена цена 1 кг корма каждого вида.
Составить рацион, содержащий не менее нужного количества указанных питательных веществ и имеющий минимальную стоимость.