Метод отсечения. Алгоритм Гомори
Общая задача линейного дискретного целочисленного программирования имеет вид:xj ≥ 0 , j = 1,..,n (4.3)
xj– целые, j = 1,..,n (4.4)
Задача (4.1) – (4.4) называется полностью целочисленной задачей линейного программирования, т.к. на все переменные положено условие целочисленности (ограничение 4.4). Когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной.
Пусть дана задача полностью целочисленного линейного программирования (4.1) – (4.4). Алгоритм метода отсечений состоит из следующих этапов:
1) решается ЗЛП (4.1) – (4.3) с отброшенными условием целочисленности (4.4); если она не разрешима, то задача (4.1) –(4.4) тоже решения не имеет;
2) если условие целочисленности выполняется по всем переменным, то найденное решение есть решение задачи (4.1) –(4.4);
3) иначе строится дополнительное отсекающее ограничение, включается в систему ограничений (4.2) – (4.3) и на этап 1.
Для решения полностью целочисленной задачи ЛП Гомори предложено делать каждый раз на этапе 3 дополнительное ограничение для нецелой переменной с наибольшей дробной частью.
Предположим, что задача с отброшенным условием целочисленности решена. Рассмотрим i-ю строку оптимальной симплексной таблицы, которой соответствует нецелое решение β i базисной переменной xi Пусть R – множество индексов j, которые соответствуют небазисным переменным. Тогда переменная xi может быть выражена через небазисные переменные xj:
Обозначим наибольшую целую часть числа a, его не превосходящую, через [a], ( a≥[a]), а дробную положительную часть – через {a} Очевидно a = [a] + {a}. Например, если a=4,7 то [a] = 4, {a} = 0,7, если a =-8,6, то [a] = -9, {a} = 0,4.
Выразим базисную переменную xi в (4.5) в виде суммы целой и дробной частей.
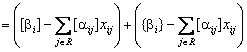 .(4.6)
.(4.6)
Выражение в левых круглых скобках (4.6) целое число, и чтобы xj было целым, необходимо, чтобы выражение в правых круглых скобках (4.6) тоже было целым. Когда выражение
Соотношение (4.7) определяет правильное отсечение Гомори.
Задача (4.1) – (4.4) не будет иметь полностью целочисленного решения, если встретится в симплекс-таблице уравнение такое, что βi дробное число, а αij –целые.
Пример решения методом Гомори
Решить задачу ЛП max: Z = 3 x1 + x 2
при ограничениях: 3x1 – 2x2 ≤3
-5 x1 – 4x 2 ≤ -10;
2 x1 + x 2 ≤ 5;
x1, x 2 ≥ 0
x1, x 2 – целые.
Без учета целочисленности оптимальной симплекс-таблицей будет следующая табл. 4.1.
Решим прямую задачу линейного программирования симплексным методом, с использованием калькулятора.
Поскольку в правой части присутствуют отрицательные значения, умножим соответствующие строки на (-1).
Определим максимальное значение целевой функции F(X) = 3x1 + x2 при следующих условиях-ограничений.
3x1 - 2x2≤3
5x1 + 4x2≥10
2x1 + x2≤5
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
3x1-2x2 + 1x3 + 0x4 + 0x5 = 3
5x1 + 4x2 + 0x3-1x4 + 0x5 = 10
2x1 + 1x2 + 0x3 + 0x4 + 1x5 = 5
Введем искусственные переменные x.
3x1-2x2 + 1x3 + 0x4 + 0x5 + 0x6 = 3
5x1 + 4x2 + 0x3-1x4 + 0x5 + 1x6= 10
2x1 + 1x2 + 0x3 + 0x4 + 1x5 + 0x6= 5
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = 3x1+x2 - Mx6 => max
Из уравнений выражаем искусственные переменные:
x6 = 10-5x1-4x2+x4
которые подставим в целевую функцию:
F(X) = (3+5M)x1+(1+4M)x2+(-1M)x4+(-10M) => max
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

Решим систему уравнений относительно базисных переменных:
x3, x6, x5,
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,3,0,5,10)
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| 0 | x3 | 3 | 3 | -2 | 1 | 0 | 0 | 0 |
| x6 | 10 | 5 | 4 | 0 | -1 | 0 | 1 | |
| x5 | 5 | 2 | 1 | 0 | 0 | 1 | 0 | |
| Индексная строка | F(X0) | -10M | -3-5M | -1-4M | 0 | 1M | 0 | 0 |
Переходим к основному алгоритму симплекс-метода.
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 1 | x3 | 3 | 3 | -2 | 1 | 0 | 0 | 0 | 1 |
| x6 | 10 | 5 | 4 | 0 | -1 | 0 | 1 | 2 | |
| x5 | 5 | 2 | 1 | 0 | 0 | 1 | 0 | 21/2 | |
| Индексная строка | F(X1) | -10M | -3-5M | -1-4M | 0 | 1M | 0 | 0 | 0 |
Итерация №0.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент.
Вычислим значения Diпо строкам как частное от деления:
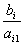
и из них выберем наименьшее:
min (3 : 3 , 10 : 5 , 5 : 2 ) = 1
Следовательно, 1-ая строка является ведущей.
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 2 | x1 | 1 | 1 | -2/3 | 1/3 | 0 | 0 | 0 | - |
| x6 | 5 | 0 | 71/3 | -12/3 | -1 | 0 | 1 | 15/22 | |
| x5 | 3 | 0 | 21/3 | -2/3 | 0 | 1 | 0 | 12/7 | |
| Индексная строка | F(X2) | 3-5M | 0 | -3-71/3M | 1+12/3M | 1M | 0 | 0 | 0 |
Итерация №1.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент.
Вычислим значения Diпо строкам как частное от деления:
и из них выберем наименьшее:
min (- , 5 : 71/3, 3 : 21/3) =15/22
Следовательно, 2-ая строка является ведущей.
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 3 | x1 | 15/11 | 1 | 0 | 2/11 | -1/11 | 0 | 1/11 | - |
| x2 | 15/22 | 0 | 1 | -5/22 | -3/22 | 0 | 3/22 | - | |
| x5 | 19/22 | 0 | 0 | -3/22 | 7/22 | 1 | -7/22 | 43/7 | |
| Индексная строка | F(X3) | 51/22 | 0 | 0 | 7/22 | -9/22 | 0 | 9/22+1M | 0 |
Итерация №2.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x4, так как это наибольший коэффициент.
Вычислим значения Diпо строкам как частное от деления:
и из них выберем наименьшее:
min (- , - , 19/22:7/22) = 43/7
Следовательно, 3-ая строка является ведущей.
Конец итераций: найден оптимальный план
Окончательный вариант симплекс-таблицы:
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| 4 | x1 | 16/7 | 1 | 0 | 1/7 | 0 | 2/7 | 0 |
| x2 | 12/7 | 0 | 1 | -2/7 | 0 | 3/7 | 0 | |
| x4 | 43/7 | 0 | 0 | -3/7 | 1 | 31/7 | -1 | |
| Индексная строка | F(X4) | 66/7 | 0 | 0 | 1/7 | 0 | 12/7 | 1M |
Оптимальный план можно записать так:
x1= 16/7
x2= 12/7
x4= 43/7
F(X) = 3•16/7+ 1•12/7= 66/7
В полученном оптимальном плане присутствуют дробные числа.
По 1-у уравнению с переменной x1, получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью6/7, составляем дополнительное ограничение:
q1- q11•x1- q12•x2- q13•x3- q14•x4- q15•x5- q16•x6≤0
q1= b1- [b1] = 16/7- 1 =6/7
q11= a11- [a11] = 1 - 1 = 0
q12= a12- [a12] = 0 - 0 = 0
q13= a13- [a13] =1/7- 0 =1/7
q14= a14- [a14] = 0 - 0 = 0
q15= a15- [a15] =2/7- 0 =2/7
q16= a16- [a16] = 0 - 0 = 0
Дополнительное ограничение имеет вид:
6/7-1/7x3-2/7x5≤0
Преобразуем полученное неравенство в уравнение:
6/7-1/7x3-2/7x5+ x7= 0
коэффициенты которого введем дополнительной строкой в оптимальную симплексную таблицу.
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 0 | x1 | 16/7 | 1 | 0 | 1/7 | 0 | 2/7 | 0 | 0 |
| x2 | 12/7 | 0 | 1 | -2/7 | 0 | 3/7 | 0 | 0 | |
| x4 | 43/7 | 0 | 0 | -3/7 | 1 | 31/7 | -1 | 0 | |
| x7 | -6/7 | 0 | 0 | -1/7 | 0 | -2/7 | 0 | 1 | |
| Индексная строка | F(X0) | -10M | -3-5M | -1-4M | 0 | 1M | 0 | 0 | 0 |
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 4-ая строка, а переменную x7следует вывести из базиса.
В строку θ заносим следующие величины:
[ - ; - ;1/7:-1/7; - ;12/7:-2/7; - ; - ;] = [ - ; -;-1; - ;-41/2; - ; - ;]
Минимальное значение θ соответствует 3-му столбцу, т.е. переменную x3необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный-1/7.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 |
| 16/7-(-6/7• 1/7):-1/7 | 1-(0 • 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 1 /7-(-1/7• 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 2 /7-(-2/7• 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 0-(1 • 1/7):-1/7 |
| 12/7-(-6/7• -2/7):-1/7 | 0-(0 • -2/7):-1/7 | 1-(0 • -2/7):-1/7 | -2 /7-(-1/7• -2/7):-1/7 | 0-(0 • -2/7):-1/7 | 3 /7-(-2/7• -2/7):-1/7 | 0-(0 • -2/7):-1/7 | 0-(1 • -2/7):-1/7 |
| 43/7-(-6/7• -3/7):-1/7 | 0-(0 • -3/7):-1/7 | 0-(0 • -3/7):-1/7 | -3/7-(-1/7• -3/7):-1/7 | 1-(0 • -3/7):-1/7 | 31/7-(-2/7• -3/7):-1/7 | -1-(0 • -3/7):-1/7 | 0-(1 • -3/7):-1/7 |
| -6/7: -1/7 | 0 : -1/7 | 0 : -1/7 | -1/7: -1/7 | 0 : -1/7 | -2/7: -1/7 | 0 : -1/7 | 1 : -1/7 |
| 66/7-(-6/7• 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 1/7-(-1/7• 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 12/7-(-2/7• 1/7):-1/7 | 10000-(0 • 1/7):-1/7 | 0-(1 • 1/7):-1/7 |
| План | Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 0 | x1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| x2 | 3 | 0 | 1 | 0 | 0 | 1 | 0 | -2 | |
| x4 | 7 | 0 | 0 | 0 | 1 | 4 | -1 | -3 | |
| x3 | 6 | 0 | 0 | 1 | 0 | 2 | 0 | -7 | |
| Индексная строка | F(X0) | -10M | -3-5M | -1-4M | 0 | 1M | 0 | 0 | 0 |
Решение получилось целочисленным. Нет необходимости применять метод Гомори.
Оптимальный целочисленный план можно записать так: x1= 1, x2= 3, x4= 7, x3= 6; F(X) = 6
Пример №2. Решить методом отсечений следующую целочисленную задачу ЛП:
7x1 + 9x2 → max
- x1 + 3x2≤6
7x1 + x2≤35
- x1 + 3x2≤6
1 ≥ x2 ≥
1, x2 - целые
7x1 + 9x2 → max
- x1 + 3x2≤6
7x1 + x2≤35
- x1 + 3x2≤6
Решаем задачу L0 симплекс-методом.
Определим максимальное значение целевой функции F(X) = 7x1 + 9x2 при следующих условиях-ограничений.
- x1 + 3x2≤6
7x1 + x2≤35
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x3. В 2-м неравенстве смысла (≤) вводим базисную переменную x4.
-1x1 + 3x2 + 1x3 + 0x4 = 6
7x1 + 1x2 + 0x3 + 1x4 = 35
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| A = |
|
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Экономический смысл дополнительных переменных: дополнительные переменные задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Решим систему уравнений относительно базисных переменных: x3, x4
Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,6,35)
Базисное решение называется допустимым, если оно неотрицательно.
| Базис | B | x1 | x2 | x3 | x4 |
| x3 | 6 | -1 | 3 | 1 | 0 |
| x4 | 35 | 7 | 1 | 0 | 1 |
| F(X0) | 0 | -7 | -9 | 0 | 0 |
Переходим к основному алгоритму симплекс-метода.
В полученном оптимальном плане присутствуют дробные числа. Определяем первое правильное отсечение.
По 1-у уравнению с переменной x2, получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью 1/2, составляем дополнительное ограничение:
q1 - q11•x1 - q12•x2 - q13•x3 - q14•x4≤0
q1 = b1 - [b1] = 31/2 - 3 = 1/2
q11 = a11 - [a11] = 0 - 0 = 0
q12 = a12 - [a12] = 1 - 1 = 0
q13 = a13 - [a13] = 7/22 - 0 = 7/22
q14 = a14 - [a14] = 1/22 - 0 = 1/22
Дополнительное ограничение имеет вид:
1/2-7/22x3-1/22x4 ≤ 0
Преобразуем полученное неравенство в уравнение:
1/2-7/22x3-1/22x4 + x5 = 0
коэффициенты которого введем дополнительной строкой в оптимальную симплексную таблицу.
Поскольку двойственный симплекс-метод используется для поиска минимума целевой функции, делаем преобразование F(x) = -F(X).
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 7/2 | 0 | 1 | 7/22 | 1/22 | 0 |
| x1 | 9/2 | 1 | 0 | -1/22 | 3/22 | 0 |
| x5 | -1/2 | 0 | 0 | -7/22 | -1/22 | 1 |
| F(X0) | -63 | 0 | 0 | -28/11 | -15/11 | 0 |
1. Проверка критерия оптимальности.
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
2. Определение новой свободной переменной.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 3-ая строка, а переменную x5 следует вывести из базиса.
3. Определение новой базисной переменной.
Минимальное значение θ соответствует 3-му столбцу, т.е. переменную x3 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-7/22).
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 31/2 | 0 | 1 | 7/22 | 1/22 | 0 |
| x1 | 41/2 | 1 | 0 | -1/22 | 3/22 | 0 |
| x5 | -1/2 | 0 | 0 | -7/22 | -1/22 | 1 |
| F(X0) | -63 | 0 | 0 | -26/11 | -14/11 | 0 |
| θ | - | - | -26/11 : (-7/22) = 8 | -14/11 : (-1/22) = 30 | - |
4. Пересчет симплекс-таблицы.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 3 | 0 | 1 | 0 | 0 | 1 |
| x1 | 32/7 | 1 | 0 | 0 | 1/7 | -1/7 |
| x3 | 11/7 | 0 | 0 | 1 | 1/7 | -22/7 |
| F(X0) | -59 | 0 | 0 | 0 | -1 | -8 |
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 | x 5 |
| 31/2-(-1/2 • 7/22):-7/22 | 0-(0 • 7/22):-7/22 | 1-(0 • 7/22):-7/22 | 7/22-(-7/22 • 7/22):-7/22 | 1/22-(-1/22 • 7/22):-7/22 | 0-(1 • 7/22):-7/22 |
| 41/2-(-1/2 • -1/22):-7/22 | 1-(0 • -1/22):-7/22 | 0-(0 • -1/22):-7/22 | -1/22-(-7/22 • -1/22):-7/22 | 3/22-(-1/22 • -1/22):-7/22 | 0-(1 • -1/22):-7/22 |
| -1/2 : -7/22 | 0 : -7/22 | 0 : -7/22 | -7/22 : -7/22 | -1/22 : -7/22 | 1 : -7/22 |
| -63-(-1/2 • -26/11):-7/22 | 0-(0 • -26/11):-7/22 | 0-(0 • -26/11):-7/22 | -26/11-(-7/22 • -26/11):-7/22 | -14/11-(-1/22 • -26/11):-7/22 | 0-(1 • -26/11):-7/22 |
В полученном оптимальном плане присутствуют дробные числа.
По 2-у уравнению с переменной x1, получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью 4/7, составляем дополнительное ограничение:
q2 - q21•x1 - q22•x2 - q23•x3 - q24•x4 - q25•x5≤0
q2 = b2 - [b2] = 44/7 - 4 = 4/7
q21 = a21 - [a21] = 1 - 1 = 0
q22 = a22 - [a22] = 0 - 0 = 0
q23 = a23 - [a23] = 0 - 0 = 0
q24 = a24 - [a24] = 1/7 - 0 = 1/7
q25 = a25 - [a25] = -1/7 + 1 = 6/7
Дополнительное ограничение имеет вид:
4/7-1/7x4-6/7x5 ≤ 0
Преобразуем полученное неравенство в уравнение:
4/7-1/7x4-6/7x5 + x6 = 0
коэффициенты которого введем дополнительной строкой в оптимальную симплексную таблицу.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 3 | 0 | 1 | 0 | 0 | 1 | 0 |
| x1 | 32/7 | 1 | 0 | 0 | 1/7 | -1/7 | 0 |
| x3 | 11/7 | 0 | 0 | 1 | 1/7 | -22/7 | 0 |
| x6 | -4/7 | 0 | 0 | 0 | -1/7 | -6/7 | 1 |
| F(X0) | -59 | 0 | 0 | 0 | -1 | -8 | 0 |
1. Проверка критерия оптимальности.
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
2. Определение новой свободной переменной.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 4-ая строка, а переменную x6 следует вывести из базиса.
3. Определение новой базисной переменной.
Минимальное значение θ соответствует 4-му столбцу, т.е. переменную x4 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-1/7).
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 3 | 0 | 1 | 0 | 0 | 1 | 0 |
| x1 | 44/7 | 1 | 0 | 0 | 1/7 | -1/7 | 0 |
| x3 | 14/7 | 0 | 0 | 1 | 1/7 | -31/7 | 0 |
| x6 | -4/7 | 0 | 0 | 0 | -1/7 | -6/7 | 1 |
| F(X0) | -59 | 0 | 0 | 0 | -1 | -8 | 0 |
| θ | - | - | - | -1 : (-1/7) = 7 | -8 : (-6/7) = 91/3 | - |
4. Пересчет симплекс-таблицы.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 3 | 0 | 1 | 0 | 0 | 1 | 0 |
| x1 | 4 | 1 | 0 | 0 | 0 | -1 | 1 |
| x3 | 1 | 0 | 0 | 1 | 0 | -4 | 1 |
| x4 | 4 | 0 | 0 | 0 | 1 | 6 | -7 |
| F(X0) | -55 | 0 | 0 | 0 | 0 | -2 | -7 |
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 |
| 3-(-4/7 • 0):-1/7 | 0-(0 • 0):-1/7 | 1-(0 • 0):-1/7 | 0-(0 • 0):-1/7 | 0-(-1/7 • 0):-1/7 | 1-(-6/7 • 0):-1/7 | 0-(1 • 0):-1/7 |
| 44/7-(-4/7 • 1/7):-1/7 | 1-(0 • 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 1/7-(-1/7 • 1/7):-1/7 | -1/7-(-6/7 • 1/7):-1/7 | 0-(1 • 1/7):-1/7 |
| 14/7-(-4/7 • 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 0-(0 • 1/7):-1/7 | 1-(0 • 1/7):-1/7 | 1/7-(-1/7 • 1/7):-1/7 | -31/7-(-6/7 • 1/7):-1/7 | 0-(1 • 1/7):-1/7 |
| -4/7 : -1/7 | 0 : -1/7 | 0 : -1/7 | 0 : -1/7 | -1/7 : -1/7 | -6/7 : -1/7 | 1 : -1/7 |
| -59-(-4/7 • -1):-1/7 | 0-(0 • -1):-1/7 | 0-(0 • -1):-1/7 | 0-(0 • -1):-1/7 | -1-(-1/7 • -1):-1/7 | -8-(-6/7 • -1):-1/7 | 0-(1 • -1):-1/7 |
Решение получилось целочисленным. Нет необходимости применять метод Гомори.
Оптимальный целочисленный план можно записать так: x2 = 3, x1 = 4, x3 = 1, x4 = 4;F(X) = 55
Пример №3. Решить целочисленную задачу линейного программирования, используя метод Гомори: F(X) = 8x1 + 5x2
5x1 + 2x2≤20
x1 + x2≤6
Решение находим с помощью калькулятора.
Этап I. Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 8x1 + 5x2 при следующих условиях-ограничений.
5x1 + 2x2≤20
x1 + x2≤6
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
5x1 + 2x2 + 1x3 + 0x4 = 20
1x1 + 1x2 + 0x3 + 1x4 = 6
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Решим систему уравнений относительно базисных переменных: x3, x4,
Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,20,6)
|
План |
Базис |
B |
x1 |
x2 |
x3 |
x4 |
|
0 |
x3 |
20 |
5 |
2 |
1 |
0 |
|
|
x4 |
6 |
1 |
1 |
0 |
1 |
|
Индексная строка |
F(X0) |
0 |
-8 |
-5 |
0 |
0 |
Посмотреть все итерации
Оптимальный план можно записать так:
x1 = 22/3, x2 = 31/3. F(X) = 8•22/3 + 5•31/3 = 38
Этап II. В полученном оптимальном плане присутствуют дробные числа. Используем метод Гомори.
По 1-у уравнению с переменной x1, получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью 2/3, составляем дополнительное ограничение:
q1 - q11•x1 - q12•x2 - q13•x3 - q14•x4≤0
q1 = b1 - [b1] = 22/3 - 2 = 2/3
q11 = a11 - [a11] = 1 - 1 = 0
q12 = a12 - [a12] = 0 - 0 = 0
q13 = a13 - [a13] = 1/3 - 0 = 1/3
q14 = a14 - [a14] = -2/3 + 1 = 1/3
Дополнительное ограничение имеет вид:
2/3-1/3x3-1/3x4≤0
Преобразуем полученное неравенство в уравнение:
2/3-1/3x3-1/3x4 + x5 = 0
коэффициенты которого введем дополнительной строкой в оптимальную симплексную таблицу.
|
План |
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
|
0 |
x1 |
22/3 |
1 |
0 |
1/3 |
-2/3 |
0 |
|
|
x2 |
31/3 |
0 |
1 |
-1/3 |
12/3 |
0 |
|
|
x5 |
-2/3 |
0 |
0 |
-1/3 |
-1/3 |
1 |
|
Индексная строка |
F(X0) |
38 |
0 |
0 |
1 |
3 |
0 |
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 3-ая строка, а переменную x5 следует вывести из базиса.
В строку θ заносим следующие величины:
[ - ; - ;1:-1/3;3:-1/3; - ;] = [ - ; - ;-3;-9; - ;]
Минимальное значение θ соответствует 3-му столбцу, т.е. переменную x3 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный -1/3.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Представим расчет каждого элемента в виде таблицы:
|
B |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
|
22/3-(-2/3 • 1/3):-1/3 |
1-(0 • 1/3):-1/3 |
0-(0 • 1/3):-1/3 |
1/3-(-1/3 • 1/3):-1/3 |
-2/3-(-1/3 • 1/3):-1/3 |
0-(1 • 1/3):-1/3 |
|
31/3-(-2/3 • -1/3):-1/3 |
0-(0 • -1/3):-1/3 |
1-(0 • -1/3):-1/3 |
-1/3-(-1/3 • -1/3):-1/3 |
12/3-(-1/3 • -1/3):-1/3 |
0-(1 • -1/3):-1/3 |
|
-2/3 : -1/3 |
0 : -1/3 |
0 : -1/3 |
-1/3 : -1/3 |
-1/3 : -1/3 |
1 : -1/3 |
|
38-(-2/3 • 1):-1/3 |
0-(0 • 1):-1/3 |
0-(0 • 1):-1/3 |
1-(-1/3 • 1):-1/3 |
3-(-1/3 • 1):-1/3 |
0-(1 • 1):-1/3 |
|
План |
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
|
0 |
x1 |
2 |
1 |
0 |
0 |
-1 |
1 |
|
|
x2 |
4 |
0 |
1 |
0 |
2 |
-1 |
|
|
x3 |
2 |
0 |
0 |
[ |
1 |
-3 |
|
Индексная строка |
F(X0) |
36 |
0 |
0 |
[ |
2 |
3 |
Решение получилось целочисленным. Нет необходимости применять метод Гомори.
Оптимальный план можно записать так: x1 = 2, x2 = 4, x3 = 2
F(X) = 36
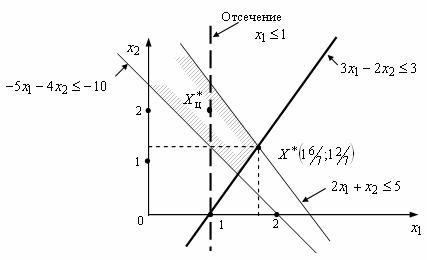
Пример №4. Найти полностью целочисленное решение следующих задач, сопровождая (где это возможно) решение графической иллюстрацией. Предполагается, что все Xk≥0.
Пример №5. Решить целочисленную задачу линейного программирования, используя метод Гомори: F(X) = x1 + 2x2
4x1 + 3x2≤24
-x1 + x2≤3
Решение находим с помощью сервиса Метод Гомори
(случай целочисленного решения).
Этап I. Решим прямую задачу линейного программирования симплекс-методом.
Определим максимальное значение целевой функции F(X) = x1 + 2x2 при следующих условиях-ограничений.
4x1 + 3x2≤24
-x1 + x2≤3
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
4x1 + 3x2 + 1x3 + 0x4 = 24
-1x1 + 1x2 + 0x3 + 1x4 = 3
Введем новую переменную x0 = x1 + 2x2.
Выразим базисные переменные <3, 4> через небазисные.
x0 = 0+x1+2x2
x3 = 24-4x1-3x2
x4 = 3+x1-x2
Переходим к основному алгоритму симплекс-метода.
Поскольку задача решается на максимум, то переменную для включения в текущий план выбирают по максимальному положительному числу в уравнении для x0.
x0 = 0+x1+2x2
x3 = 24-4x1-3x2
x4 = 3+x1-x2
В качестве новой переменной выбираем x2.
Вычислим значения D2 по всем уравнениям для этой переменной.
и из них выберем наименьшее:
min (24 : 3 , 3 : 1 ) = 3
Вместо переменной x4 в план войдет переменная x2.
Выразим переменную x2 через x4 и подставим во все выражения.
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = 6+3x1-2x4
x3 = 15-7x1+3x4
x2 = 3+x1-x4
Полагая небазисные переменные x = (3, 2) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (-3, 0, 0, 2), x0 = 6
x0 = 6+3x1-2x4
x3 = 15-7x1+3x4
x2 = 3+x1-x4
В качестве новой переменной выбираем x1.
Вычислим значения D1 по всем уравнениям для этой переменной.
и из них выберем наименьшее:
min (15 : 7 , - ) = 21/7
Вместо переменной x3 в план войдет переменная x1.
Выразим переменную x1 через x3 и подставим во все выражения.
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = 123/7-3/7x3-5/7x4
x1 = 21/7-1/7x3+3/7x4
x2 = 51/7-1/7x3-4/7x4
Полагая небазисные переменные x = (1, 2) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (0, 0, 3/7, 5/7), x0 = 123/7
Выражение для x0 не содержит положительных элементов. Найден оптимальный план.
Окончательный вариант системы уравнений:
x0 = 123/7-3/7x3-5/7x4
x1 = 21/7-1/7x3+3/7x4
x2 = 51/7-1/7x3-4/7x4
Оптимальный план можно записать так:
x1 = 21/7, x2 = 51/7
F(X) = 1•21/7 + 2•51/7 = 123/7
Этап II. В полученном оптимальном плане присутствуют дробные числа. Применяем алгоритм отсечений Гомори.
По 1-у уравнению с переменной x1, получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью 1/7,
составляем дополнительное ограничение:
q1 - q11•x1 - q12•x2 - q13•x3 - q14•x4≤0
q1 = b1 - [b1] = 21/7 - 2 = 1/7
q11 = a11 - [a11] = 1 - 1 = 0
q12 = a12 - [a12] = 0 - 0 = 0
q13 = a13 - [a13] = 1/7 - 0 = 1/7
q14 = a14 - [a14] = -3/7 + 1 = 4/7
Дополнительное ограничение имеет вид:
1/7-1/7x3-4/7x4≤0
Преобразуем полученное неравенство в уравнение:
1/7-1/7x3-4/7x4 + x5 = 0
коэффициенты которого введем дополнительной строкой в оптимальную симплексную таблицу.
|
План |
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
|
0 |
x1 |
21/7 |
1 |
0 |
1/7 |
-3/7 |
0 |
|
|
x2 |
51/7 |
0 |
1 |
1/7 |
4/7 |
0 |
|
|
x5 |
-1/7 |
0 |
0 |
-1/7 |
-4/7 |
1 |
|
Индексная строка |
F(X0) |
123/7 |
0 |
0 |
3/7 |
5/7 |
0 |
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 3-ая строка, а переменную x5 следует вывести из базиса.
В строку θ заносим следующие величины:
[ - ; - ;3/7:-1/7;5/7:-4/7; - ;] = [ - ; - ;-3;-11/4; - ;]
Минимальное значение θ соответствует 4-му столбцу, т.е. переменную x4 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный -4/7.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Представим расчет каждого элемента в виде таблицы:
|
B |
x1 |
x2 |
x3 |
x4 |
x5 |
|
21/7-(-1/7 • -3/7):-4/7 |
1-(0 • -3/7):-4/7 |
0-(0 • -3/7):-4/7 |
1/7-(-1/7 • -3/7):-4/7 |
-3/7-(-4/7 • -3/7):-4/7 |
0-(1 • -3/7):-4/7 |
|
51/7-(-1/7 • 4/7):-4/7 |
0-(0 • 4/7):-4/7 |
1-(0 • 4/7):-4/7 |
1/7-(-1/7 • 4/7):-4/7 |
4/7-(-4/7 • 4/7):-4/7 |
0-(1 • 4/7):-4/7 |
|
-1/7 : -4/7 |
0 : -4/7 |
0 : -4/7 |
-1/7 : -4/7 |
-4/7 : -4/7 |
1 : -4/7 |
|
123/7-(-1/7 • 5/7):-4/7 |
0-(0 • 5/7):-4/7 |
0-(0 • 5/7):-4/7 |
3/7-(-1/7 • 5/7):-4/7 |
5/7-(-4/7 • 5/7):-4/7 |
0-(1 • 5/7):-4/7 |
|
План |
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
|
0 |
x1 |
21/4 |
1 |
0 |
1/4 |
0 |
-3/4 |
|
|
x2 |
5 |
0 |
1 |
0 |
0 |
1 |
|
|
x4 |
1/4 |
0 |
0 |
1/4 |
1 |
-13/4 |
|
Индексная строка |
F(X0) |
121/4 |
0 |
0 |
1/4 |
0 |
11/4 |
В полученном оптимальном плане присутствуют дробные числа.
По 1-у уравнению с переменной x1, получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью 1/4, составляем дополнительное ограничение:
q1 - q11•x1 - q12•x2 - q13•x3 - q14•x4 - q15•x5≤0
q1 = b1 - [b1] = 21/4 - 2 = 1/4
q11 = a11 - [a11] = 1 - 1 = 0
q12 = a12 - [a12] = 0 - 0 = 0
q13 = a13 - [a13] = 1/4 - 0 = 1/4
q14 = a14 - [a14] = 0 - 0 = 0
q15 = a15 - [a15] = -3/4 + 1 = 1/4
Дополнительное ограничение имеет вид:
1/4-1/4x3-1/4x5≤0
Преобразуем полученное неравенство в уравнение:
1/4-1/4x3-1/4x5 + x6 = 0
коэффициенты которого введем дополнительной строкой в оптимальную симплексную таблицу.
|
План |
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
0 |
x1 |
21/4 |
1 |
0 |
1/4 |
0 |
-3/4 |
0 |
|
|
x2 |
5 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
x4 |
1/4 |
0 |
0 |
1/4 |
1 |
-13/4 |
0 |
|
|
x6 |
-1/4 |
0 |
0 |
-1/4 |
0 |
-1/4 |
1 |
|
Индексная строка |
F(X0) |
121/4 |
0 |
0 |
1/4 |
0 |
11/4 |
0 |
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
Среди отрицательных значений базисных переменных выбираем наибольший по модулю.
Ведущей будет 4-ая строка, а переменную x6 следует вывести из базиса.
В строку θ заносим следующие величины:
[ - ; - ;1/4:-1/4; - ;11/4:-1/4; - ;] = [ - ; - ;-1; - ;-5; - ;]
Минимальное значение θ соответствует 3-му столбцу, т.е. переменную x3 необходимо ввести в базис.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный -1/4.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Представим расчет каждого элемента в виде таблицы:
|
B |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
21/4-(-1/4 • 1/4):-1/4 |
1-(0 • 1/4):-1/4 |
0-(0 • 1/4):-1/4 |
1/4-(-1/4 • 1/4):-1/4 |
0-(0 • 1/4):-1/4 |
-3/4-(-1/4 • 1/4):-1/4 |
0-(1 • 1/4):-1/4 |
|
5-(-1/4 • 0):-1/4 |
0-(0 • 0):-1/4 |
1-(0 • 0):-1/4 |
0-(-1/4 • 0):-1/4 |
0-(0 • 0):-1/4 |
1-(-1/4 • 0):-1/4 |
0-(1 • 0):-1/4 |
|
1/4-(-1/4 • 1/4):-1/4 |
0-(0 • 1/4):-1/4 |
0-(0 • 1/4):-1/4 |
1/4-(-1/4 • 1/4):-1/4 |
1-(0 • 1/4):-1/4 |
-13/4-(-1/4 • 1/4):-1/4 |
0-(1 • 1/4):-1/4 |
|
-1/4 : -1/4 |
0 : -1/4 |
0 : -1/4 |
-1/4 : -1/4 |
0 : -1/4 |
-1/4 : -1/4 |
1 : -1/4 |
|
121/4-(-1/4 • 1/4):-1/4 |
0-(0 • 1/4):-1/4 |
0-(0 • 1/4):-1/4 |
1/4-(-1/4 • 1/4):-1/4 |
0-(0 • 1/4):-1/4 |
11/4-(-1/4 • 1/4):-1/4 |
0-(1 • 1/4):-1/4 |
|
План |
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
0 |
x1 |
2 |
1 |
0 |
0 |
0 |
-1 |
1 |
|
|
x2 |
5 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
x4 |
0 |
0 |
0 |
0 |
1 |
-2 |
1 |
|
|
x3 |
1 |
0 |
0 |
1 |
0 |
1 |
-4 |
|
Индексная строка |
F(X0) |
12 |
0 |
0 |
0 |
0 |
1 |
1 |
Решение получилось целочисленным. Оптимальный план можно записать так:
x1 = 2, x2 = 5, x3 = 1, x4 = 0
F(X) = 12
Перейти к онлайн решению своей задачи
Пример №6. Решить следующие частично целочисленные задачи, сопровождая (где это возможно) решение графической иллюстрацией. Предполагается, что все Xj≥0, XXi≥0 – целочисленное.
Решениенаходим с помощью онлайн сервиса Метод Гомори.
Этап 1. Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = x1+ x2при следующих условиях-ограничений.
2x1+ 11x2≤38
x1+ x2≤7
4x1- 5x2≤5
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x3. В 2-м неравенстве смысла (≤) вводим базисную переменную x4. В 3-м неравенстве смысла (≤) вводим базисную переменную x5.
2x1+ 11x2+ 1x3+ 0x4+ 0x5= 38
1x1+ 1x2+ 0x3+ 1x4+ 0x5= 7
4x1-5x2+ 0x3+ 0x4+ 1x5= 5
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

Решим систему уравнений относительно базисных переменных:
x3, x4, x5,
Полагая, что свободные переменныеравны 0, получим первый опорный план:
X1 = (0,0,38,7,5)
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x3 | 38 | 2 | 11 | 1 | 0 | 0 |
| x4 | 7 | 1 | 1 | 0 | 1 | 0 |
| x5 | 5 | 4 | -5 | 0 | 0 | 1 |
| F(X0) | 0 | -1 | -1 | 0 | 0 | 0 |
Посмотреть все итерации
В полученном оптимальном плане присутствуют дробные числа.
По 1-у уравнению с переменной x2, получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью2/3, составляем дополнительное ограничение:
q1- q11•x1- q12•x2- q13•x3- q14•x4- q15•x5≤0
q1= b1- [b1] = 22/3- 2 =2/3
q11= a11- [a11] = 0 - 0 = 0
q12= a12- [a12] = 1 - 1 = 0
q13= a13- [a13] =1/9- 0 =1/9
q14= a14- [a14] =-2/9+ 1 =7/9
q15= a15- [a15] = 0 - 0 = 0
Дополнительное ограничение имеет вид:
2/3-1/9x3-7/9x4≤0
Преобразуем полученное неравенство в уравнение:
2/3-1/9x3-7/9x4+ x6= 0
коэффициенты которого введем дополнительной строкой в оптимальную симплексную таблицу.
Поскольку двойственный симплекс-методиспользуется для поиска минимума целевой функции, делаем преобразование F(x) = -F(X).
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 22/3 | 0 | 1 | 1/9 | -2/9 | 0 | 0 |
| x1 | 41/3 | 1 | 0 | -1/9 | 12/9 | 0 | 0 |
| x5 | 1 | 0 | 0 | 1 | -6 | 1 | 0 |
| x6 | -2/3 | 0 | 0 | -1/9 | -7/9 | 0 | 1 |
| F(X0) | -7 | 0 | 0 | 0 | -1 | 0 | 0 |
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-1/9).
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 22/3 | 0 | 1 | 1/9 | -2/9 | 0 | 0 |
| x1 | 41/3 | 1 | 0 | -1/9 | 12/9 | 0 | 0 |
| x5 | 1 | 0 | 0 | 1 | -6 | 1 | 0 |
| x6 | -2/3 | 0 | 0 | -1/9 | -7/9 | 0 | 1 |
| F(X) | -7 | 0 | 0 | 0 | -1 | 0 | 0 |
| θ | 0 | - | - | 0 : (-1/9) = 0 | -1 : (-7/9) = 12/7 | - | - |
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 2 | 0 | 1 | 0 | -1 | 0 | 1 |
| x1 | 5 | 1 | 0 | 0 | 2 | 0 | -1 |
| x5 | -5 | 0 | 0 | 0 | -13 | 1 | 9 |
| x3 | 6 | 0 | 0 | 1 | 7 | 0 | -9 |
| F(X0) | -7 | 0 | 0 | 0 | -1 | 0 | 0 |
На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-13).
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x2 | 2 | 0 | 1 | 0 | -1 | 0 | 1 |
| x1 | 5 | 1 | 0 | 0 | 2 | 0 | -1 |
| x5 | -5 | 0 | 0 | 0 | -13 | 1 | 9 |
| x3 | 6 | 0 | 0 | 1 | 7 | 0 | -9 |
| F(X) | -7 | 0 | 0 | 0 | -1 | 0 | 0 |
| θ | 0 | - | - | - | -1 : (-13) =1/13 | - | - |
Решение получилось целочисленным. Нет необходимости применять метод Гомори.
Оптимальный целочисленный план можно записать так: x1 = 2, x2 = 3, F(X) = 5