Симплекс-метод. Поиск наибольшего значения
Вариант 1.1. Для изготовления цемента двух видов используется сырье трех видов. Запасы сырья известны и равны соответственно: 264, 136 и 266 т. Количество сырья каждого вида, необходимое для производства единицы цемента первого вида соответственно равны: 12, 4 и 3. Для цемента второго вида: 3, 5 и 14. Прибыль от реализации цемента первого вида составляет 6 у.е., от цемента второго вида - 4 у.е. Составить план, обеспечивающий наибольшую прибыль производству:
а) записать математическую модель;
б) решить задачу графическим методом;
в) решить задачу симплекс-методом;
г) к исходной задаче записать двойственную и решить ее, используя соотношение двойственности и решение исходной.
Решение:
а) математическая модель;
x1 – производство цемента первого вида;
x2 – производство цемента второго вида;
12x1 + 3x2 ≤ 264
4x1 + 5x2 ≤ 136
3x1 + 14x2 ≤ 266
x1 ≥ 0, x2 ≥ 0
Целевая функция:
6x1 + 4x2 → max
б) решим задачу графическим методом;
Необходимо найти максимальное значение целевой функции F = 6X1+4X2 => max, при системе ограничений:
12x1+3x2≤264 (1)
4x1+5x2≤136 (2)
3x1+14x2≤266 (3)
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
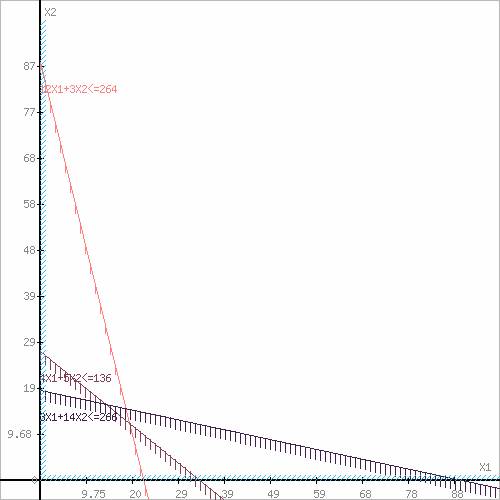
Обозначим границы области многоугольника решений.
Рассмотрим целевую функцию задачи F = 6X1+4X2 => max.
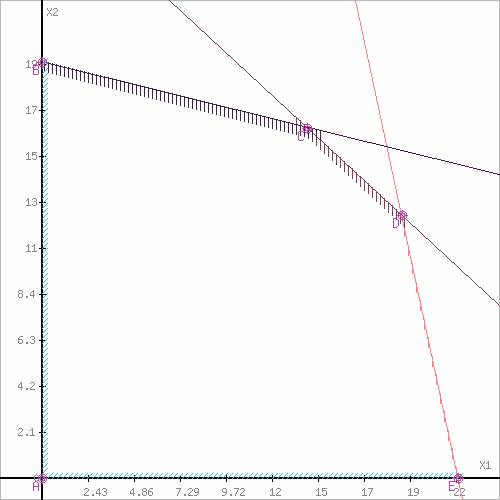
Построим прямую, отвечающую значению функции F = 0: F = 6X1+4X2
= 0. Будем двигать эту прямую параллельным образом. Поскольку нас интересует
максимальное решение, поэтому двигаем прямую до последнего касания обозначенной
области. На графике эта прямая обозначена пунктирной линией.
Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения
прямых 1 и 2, то ее координаты удовлетворяют уравнениям этих прямых:
12x1+3x2≤264
4x1+5x2≤136
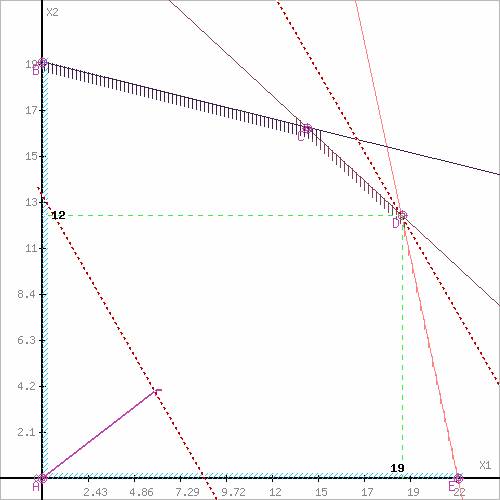
Решив систему уравнений, получим:
x1 = (264-3x2)/12
4(264-3x2)/12+5x2 = 136
x1 = 19, x2 = 12
Откуда найдем максимальное значение целевой функции:
F(X) = 6*19 + 4*12 = 162
Таким образом, чтобы получить максимальную прибыль необходимо выпускать 19 т. цемента 1-го вида, и 12 т. цемента 2-го вида.
в) решить задачу симплекс-методом;
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 6x1+4x2 при следующих условиях-ограничений.
12x1+3x2≤264
4x1+5x2≤136
3x1+14x2≤266
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
12x1 + 3x2 + 1x3 + 0x4 + 0x5 = 264
4x1 + 5x2 + 0x3 + 1x4 + 0x5 = 136
3x1 + 14x2 + 0x3 + 0x4 + 1x5 = 266
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных:
x3, x4, x5,
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,264,136,266)
|
План |
Базис |
В |
x1 |
x2 |
x3 |
x4 |
x5 |
|
0 |
x3 |
264 |
12 |
3 |
1 |
0 |
0 |
|
|
x4 |
136 |
4 |
5 |
0 |
1 |
0 |
|
|
x5 |
266 |
3 |
14 |
0 |
0 |
1 |
|
Индексная строка |
F(X0) |
0 |
-6 |
-4 |
0 |
0 |
0 |
Переходим к основному алгоритму симплекс-метода.
|
План |
Базис |
В |
x1 |
x2 |
x3 |
x4 |
x5 |
min |
|
1 |
x3 |
264 |
12 |
3 |
1 |
0 |
0 |
22 |
|
|
x4 |
136 |
4 |
5 |
0 |
1 |
0 |
34 |
|
|
x5 |
266 |
3 |
14 |
0 |
0 |
1 |
88.67 |
|
Индексная строка |
F(X1) |
0 |
-6 |
-4 |
0 |
0 |
0 |
0 |
Итерация №0.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления
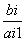и из них выберем наименьшее: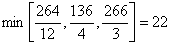
Следовательно, 1-ая строка является ведущей
Разрешающий элемент равен 12 и находится на пересечении ведущего столбца и ведущей строки
Формируем следующую часть симплексной таблицы.
Вместо переменной x3 в план 1 войдет переменная x1
Строка, соответствующая переменной x1 в плане 1, получена в результате деления всех элементов строки x3 плана 0 на разрешающий элемент РЭ=12
На месте разрешающего элемента в плане 1 получаем 1.
В остальных клетках столбца x1 плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x1 и столбец x1 .
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (12), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
|
План |
Базис |
В |
x1 |
x2 |
x3 |
x4 |
x5 |
min |
|
2 |
x1 |
22 |
1 |
0.25 |
0.0833 |
0 |
0 |
88 |
|
|
x4 |
48 |
0 |
4 |
-0.3333 |
1 |
0 |
12 |
|
|
x5 |
200 |
0 |
13.25 |
-0.25 |
0 |
1 |
15.09 |
|
Индексная строка |
F(X2) |
132 |
0 |
-2.5 |
0.5 |
0 |
0 |
0 |
Итерация №1.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления
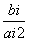и из них выберем наименьшее: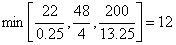
Следовательно, 2-ая строка является ведущей
Разрешающий элемент равен 4 и находится на пересечении ведущего столбца и ведущей строки
Формируем следующую часть симплексной таблицы.
Вместо переменной x4 в план 2 войдет переменная x2
Строка, соответствующая переменной x2 в плане 2, получена в результате деления всех элементов строки x4 плана 1 на разрешающий элемент РЭ=4
На месте разрешающего элемента в плане 2 получаем 1.
В остальных клетках столбца x2 плана 2 записываем нули.
Таким образом, в новом плане 2 заполнены строка x2 и столбец x2 .
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план
Окончательный вариант симплекс-таблицы:
|
План |
Базис |
В |
x1 |
x2 |
x3 |
x4 |
x5 |
|
3 |
x1 |
19 |
1 |
0 |
0.1042 |
-0.0625 |
0 |
|
|
x2 |
12 |
0 |
1 |
-0.0833 |
0.25 |
0 |
|
|
x5 |
41 |
0 |
0 |
0.8542 |
-3.31 |
1 |
|
Индексная строка |
F(X3) |
162 |
0 |
0 |
0.2917 |
0.625 |
0 |
Оптимальный план можно записать так:
x1 = 19
x2 = 12
x5 = 41
F(X) = 6*19 + 4*12 = 162
г) к исходной задаче записать двойственную и решить ее, используя соотношение двойственности и решение исходной.
Составим двойственную задачу к прямой задаче.
12y1+4y2+3y3≥6
3y1+5y2+14y3≥4
264y1+136y2+266y3 => min
y1 ≥ 0
y2 ≥ 0
y3 ≥ 0
Решение двойственной задачи дает оптимальную систему оценок ресурсов.
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
Из первой теоремы двойственности следует, что Y = C*A-1.
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.
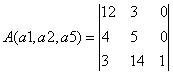
Определив обратную матрицу А-1 через алгебраические дополнения, получим:
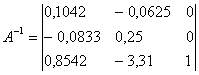
Как видно из последнего плана симплексной таблицы, обратная матрица A-1 расположена в столбцах дополнительных переменных .
Тогда Y = C*A-1 =
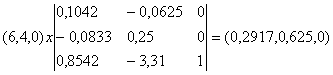
Оптимальный план двойственной задачи равен:
y1 = 0.29
y2 = 0.62
y3 = 0
Z(Y) = 264*0.29+136*0.62+266*0 = 162
2. На трех станциях отправления сосредоточен однородный груз, который следует перевезти в четыре пункта назначения, имеющих потребность в этом грузе. Стоимость перевозок единицы груза от каждой станции до каждого пункта назначения считается известной и содержится в таблице. Требуется составить такой план перевозок, при котором их общая стоимость окажется минимальной.
Решить транспортную задачу методом потенциалов.
|
Поставщик |
В1 |
В2 |
В3 |
В4 |
Запасы груза |
|
А1 |
4 |
6 |
19 |
21 |
100 |
|
А2 |
29 |
4 |
8 |
6 |
150 |
|
А3 |
7 |
11 |
13 |
14 |
200 |
|
Потребности |
220 |
80 |
75 |
75 |
|
Решение:
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
|
|
1 |
2 |
3 |
4 |
Запасы |
|
1 |
4 |
6 |
19 |
21 |
100 |
|
2 |
29 |
4 |
8 |
6 |
150 |
|
3 |
7 |
11 |
13 |
14 |
200 |
|
Потребности |
220 |
80 |
75 |
75 |
|
Проверим необходимое и достаточное условие разрешимости задачи.
∑ a = 100 + 150 + 200 = 450
∑ b = 220 + 80 + 75 + 75 = 450
Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
Занесем исходные данные в распределительную таблицу.
|
|
1 |
2 |
3 |
4 |
Запасы |
|
1 |
4 |
6 |
19 |
21 |
100 |
|
2 |
29 |
4 |
8 |
6 |
150 |
|
3 |
7 |
11 |
13 |
14 |
200 |
|
Потребности |
220 |
80 |
75 |
75 |
|
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
Искомый элемент равен 4
Для этого элемента запасы равны 100, потребности 220. Поскольку минимальным является 100, то вычитаем его.
|
4 |
x |
x |
x |
0 |
|
29 |
4 |
8 |
6 |
150 |
|
7 |
11 |
13 |
14 |
200 |
|
120 |
80 |
75 |
75 |
0 |
Искомый элемент равен 4
Для этого элемента запасы равны 150, потребности 80. Поскольку минимальным является 80, то вычитаем его.
|
4 |
x |
x |
x |
0 |
|
29 |
4 |
8 |
6 |
70 |
|
7 |
x |
13 |
14 |
200 |
|
120 |
0 |
75 |
75 |
0 |
Искомый элемент равен 6
Для этого элемента запасы равны 70, потребности 75. Поскольку минимальным является 70, то вычитаем его.
|
4 |
x |
x |
x |
0 |
|
x |
4 |
x |
6 |
0 |
|
7 |
x |
13 |
14 |
200 |
|
120 |
0 |
75 |
5 |
0 |
Искомый элемент равен 7
Для этого элемента запасы равны 200, потребности 120. Поскольку минимальным является 120, то вычитаем его.
|
4 |
x |
x |
x |
0 |
|
x |
4 |
x |
6 |
0 |
|
7 |
x |
13 |
14 |
80 |
|
0 |
0 |
75 |
5 |
0 |
Искомый элемент равен 13
Для этого элемента запасы равны 80, потребности 75. Поскольку минимальным является 75, то вычитаем его.
|
4 |
x |
x |
x |
0 |
|
x |
4 |
x |
6 |
0 |
|
7 |
x |
13 |
14 |
5 |
|
0 |
0 |
0 |
5 |
0 |
Искомый элемент равен 14
Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.
|
4 |
x |
x |
x |
0 |
|
x |
4 |
x |
6 |
0 |
|
7 |
x |
13 |
14 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
|
1 |
2 |
3 |
4 |
Запасы |
|
1 |
4[100] |
6 |
19 |
21 |
100 |
|
2 |
29 |
4[80] |
8 |
6[70] |
150 |
|
3 |
7[120] |
11 |
13[75] |
14[5] |
200 |
|
Потребности |
220 |
80 |
75 |
75 |
|
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.
2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 6. Следовательно, опорный план является невырожденным.
4. Проверим оптимальность опорного плана. Найдем потенциалы ui, vi. по занятым клеткам таблицы, в которых ui + vi = cij, полагая, что u1 = 0.
u1 + v1 = 4; 0 + v1 = 4; v1 = 4
u3 + v1 = 7; 4 + u3 = 7; u3 = 3
u3 + v3 = 13; 3 + v3 = 13; v3 = 10
u3 + v4 = 14; 3 + v4 = 14; v4 = 11
u2 + v4 = 6; 11 + u2 = 6; u2 = -5
u2 + v2 = 4; -5 + v2 = 4; v2 = 9
|
|
v1=4 |
v2=9 |
v3=10 |
v4=11 |
|
u1=0 |
4[100] |
6 |
19 |
21 |
|
u2=-5 |
29 |
4[80] |
8 |
6[70] |
|
u3=3 |
7[120] |
11 |
13[75] |
14[5] |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vi > cij
(1;2): 0 + 9 > 6; ∆12 = 0 + 9 - 6 = 3
(3;2): 3 + 9 > 11; ∆32 = 3 + 9 - 11 = 1
max(3,1) = 3
Выбираем максимальную оценку свободной клетки (1;2): 6
Для этого в перспективную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-». Цикл приведен в таблице.
|
|
1 |
2 |
3 |
4 |
Запасы |
|
1 |
4[100][-] |
6[+] |
19 |
21 |
100 |
|
2 |
29 |
4[80][-] |
8 |
6[70][+] |
150 |
|
3 |
7[120][+] |
11 |
13[75] |
14[5][-] |
200 |
|
Потребности |
220 |
80 |
75 |
75 |
|
Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 4) = 5. Прибавляем 5 к объемам грузов, стоящих в плюсовых клетках и вычитаем 5 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
|
|
1 |
2 |
3 |
4 |
Запасы |
|
1 |
4[95] |
6[5] |
19 |
21 |
100 |
|
2 |
29 |
4[75] |
8 |
6[75] |
150 |
|
3 |
7[125] |
11 |
13[75] |
14 |
200 |
|
Потребности |
220 |
80 |
75 |
75 |
|
4. Проверим оптимальность опорного плана. Найдем потенциалы ui, vi. по занятым клеткам таблицы, в которых ui + vi = cij, полагая, что u1 = 0.
u1 + v1 = 4; 0 + v1 = 4; v1 = 4
u3 + v1 = 7; 4 + u3 = 7; u3 = 3
u3 + v3 = 13; 3 + v3 = 13; v3 = 10
u1 + v2 = 6; 0 + v2 = 6; v2 = 6
u2 + v2 = 4; 6 + u2 = 4; u2 = -2
u2 + v4 = 6; -2 + v4 = 6; v4 = 8
|
|
v1=4 |
v2=6 |
v3=10 |
v4=8 |
|
u1=0 |
4[95] |
6[5] |
19 |
21 |
|
u2=-2 |
29 |
4[75] |
8 |
6[75] |
|
u3=3 |
7[125] |
11 |
13[75] |
14 |
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui+ vi <= cij.
Минимальные затраты составят:
F(x) = 4*95 + 6*5 + 4*75 + 6*75 + 7*125 + 13*75 = 3010