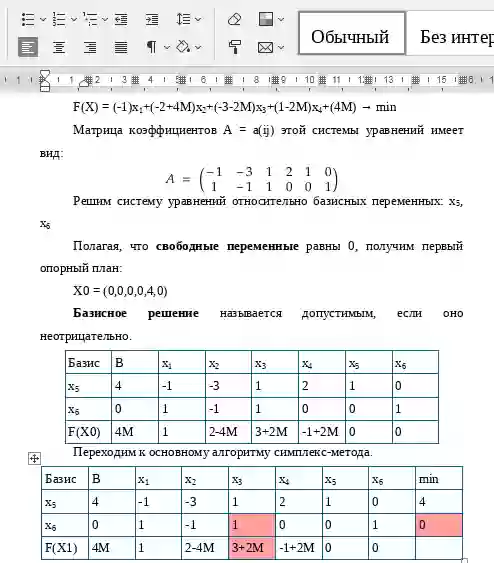
Симплексный метод решения ЗЛП
Симплекс-метод - это итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения, улучшающих значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения.Назначение сервиса. Сервис предназначен для онлайн решения задач линейного программирования (ЗЛП) симплекс-методом в следующих формах записи:
- в виде симплексной таблицы (метод жордановых преобразований); базовой форме записи;
- модифицированным симплекс-методом; в столбцовой форме; в строчечной форме.
Графический метод решения ЗЛП
Решение транспортной задачи
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X)зависит от количества реализованных партий товара Х и представлен в таблице.
| Объем товара Х (в партиях) | Доход G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
Алгоритм симплекс-метода включает следующие этапы:
- Составление первого опорного плана. Переход к канонической форме задачи линейного программирования путем введения неотрицательных дополнительных балансовых переменных.
- Проверка плана на оптимальность. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить.
- Определение ведущих столбца и строки. Из отрицательных коэффициентов индексной строки выбирается наибольший по абсолютной величине. Затем элементы столбца свободных членов симплексной таблицы делит на элементы того же знака ведущего столбца.
- Построение нового опорного плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана—Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | min |
| x3 | 20 | 5 | 2 | 1 | 0 | 20:5=4 |
| x4 | 6 | 1 | 1 | 0 | 1 | 6:1=6 |
| F(X1) | -8 | -5 | 0 | 0 | 0 |
Если необходимо найти экстремум целевой функции, то речь идет о поиске минимального значения (
F(x) → min, см. пример решения минимизации функции) и максимального значения (F(x) → max, см. пример решения максимизации функции)
Экстремальное решение достигается на границе области допустимых решений в одной из вершин угловых точек многоугольника, либо на отрезке между двумя соседними угловыми точками.
Основная теорема линейного программирования. Если целевая функция ЗЛП достигает экстремального значения в некоторой точке области допустимых решений, то она принимает это значение в угловой точке. Если целевая функция ЗЛП достигает экстремального значения более чем в одной угловой точке, то она принимает это же значение в любой из выпуклой линейной комбинации этих точек.
Суть симплекс-метода. Движение к точке оптимума осуществляется путем перехода от одной угловой точки к соседней, которая ближе и быстрее приближает к Xопт. Такую схему перебора точек, называемую симплекс-метод, предложил Р. Данцигом.
Угловые точки характеризуются m базисными переменными, поэтому переход от одной угловой точки к соседней возможно осуществить сменой в базисе только одной базисной переменной на переменную из небазиса.
Реализация симплекс-метода в силу различных особенностей и постановок задач ЛП имеет различные модификации.
Построение симплекс-таблиц продолжается до тех пор, пока не будет получено оптимальное решение.
Как с помощью симплекс-таблицы определить, что решение задачи линейного программирования является оптимальным?
Если последняя строка (значения целевой функции) не содержит отрицательных элементов, следовательно, найдет оптимальный план.
Замечание 1. Если одна из базисных переменных равна нулю, то крайняя точка, соответствующая такому базисному решению - вырожденная. Вырожденность возникает, когда имеется неоднозначность в выборе направляющей строки. Можно вообще не заметить вырожденности задачи, если выбрать другую строку в качестве направляющей. В случае неоднозначности нужно выбирать строку с наименьшим индексом, чтобы избежать зацикливания.
Замечание 2. Пусть в некоторой крайней точке все симплексные разности неотрицательные Dk³ 0 (k = 1..n+m),т.е. получено оптимальное решение и существует такой Аk – небазисный вектор, у которого Dk = 0. Тогда максимум достигается по крайней мере в двух точках, т.е. имеет место альтернативный оптимум. Если ввести в базис эту переменную xk, значение целевой функции не изменится.
Замечание 3. Решение двойственной задачи находится в последней симплексной таблице. Последние m компонент вектора симплексных разностей( в столбцах балансовых переменных) – оптимальное решение двойственной задачи. Значение целевых функций прямой и двойственной задачи в оптимальных точках совпадают.
Замечание 4. При решении задачи минимизации в базис вводится вектор с наибольшей положительной симплексной разностью. Далее применяется тот же алгоритм, что и для задачи максимизации.
Если задано условие «Необходимо, чтобы сырье III вида было израсходовано полностью», то соответствующее условие представляет собой равенство.
Аналитическое введение в симплекс-метод
Симплексный метод является универсальным методом линейного программирования.Итак, если мы решаем ЗЛП в канонической форме, то система ограничений - это обычная система линейных уравнений. При решении задач ЛП получаются системы линейных уравнений, имеющие, как правило, бесконечно много решений.
Например, пусть дана система
![]()
Здесь число уравнений равно 2, а неизвестных - 3, уравнений меньше. Выразим x1 и x2 через x3:
![]()
Это общее решение системы. если переменной x3 придавать произвольные числовые значения, то будем находить частные решения системы. Например, x3=1 → x1=1 → x2=6. Имеем (1, 6, 1) - частное решение. Пусть x3=2 → x1=-3, x2= 1, (-3, 1, 2) - другое частное решение. Таких частных решений бесконечно много.
Переменные x1 и x2 называются базисными, а переменная x3 - не базисная, свободная.
Совокупность переменных x1 и x2 образует базис: Б (x1, x2). Если x3 = 0, то полученное частное решение (5, 11, 0) называется базисным решением, соответствующим базису Б (x1, x2).
Базисным называется решение, соответствующее нулевым значениям свободных переменных.
В качестве базисных можно было взять и другие переменные: (x1, x3) или (x2, x3).
Как переходить от одного базиса Б(x1, x2) к другому базису Б(x1, x3)?
Для этого надо переменную x3 перевести в базисные, а x2 - в небазисные т. е. в уравнениях надо x3 выразить через x2 и подставить в 1-е:
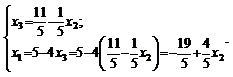
Базисное решение, соответствующее базису Б (x1, x3), таково: (-19/5; 0; 11/5).
Если теперь от базиса Б (x1, x3) нам захочется перейти к базису Б (x2, x3), то
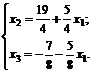
Базисное решение, соответствующее базису Б (x2, x3): (0;19/4; 7/8).
Из трех найденных базисных решений решение, соответствующее базису Б (x1, x3) - отрицательное x1 < 0, нас в ЗЛП интересуют только неотрицательные решения.
Если задача ЛП имеет решение, то оно достигается на множестве базисных неотрицательных решений системы ограничений канонической формы.
Поэтому идея симплекс-метода и состоит в последовательном переходе от одного базиса к другому, лучшему с точки зрения значения целевой функции.
Пример. Решить задачу ЛП.
Функцию F= x2 - x1 → min необходимо минимизировать при заданной системе ограничений:
-2x1 + x2 + x3 = 2
x1 + x2 + x5 = 5
x1 - 2x2 + x4 = 12
xi ≥ 0, i = 1, 5
Эти ограничения могут рассматриваться как произошедшие из неравенств, а переменные x3, x5, x4 - как дополнительные.
Запишем ограничения, выбрав базис из переменных Б{ x3, , x4, x5}:
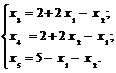
Этому базису соответствует базисное неотрицательное решение
x1 = 0, x2 = 0, x3 = 2, x4 = 2, x5 = 5 или (0, 0, 2, 2, 5).
Теперь нужно выразить F через небазисные переменные, в нашем случае это уже сделано: F= x2 - x1.
Проверим, достигла ли функция F своего минимального значения. Для этого базисного решения F= 0 - 0 = 0 - значение функции равно 0. Но его можно уменьшить, если x1 будет возрастать, т. к. коэффициент в функции при x1 отрицателен. Однако при увеличении x1 значения переменных x4, x5 уменьшаются (смотрите второе и третье равенство системы ограничений). Переменная x1 не может быть увеличена больше чем до 2, иначе x4 станет отрицательной (ввиду равенства 2), и не больше, чем до 5, иначе x5 - отрицателен. Итак, из анализа равенств следует, что переменную x1 можно увеличить до 2, при этом значение функции уменьшится.
Перейдем к новому базису Б2, введя переменную x1 в базис вместо x4.
Б2{x1, x3, x5}.
Выразим эти базисные переменные через небазисные. Для этого сначала выразим x1 из второго уравнения и подставим в остальные, в том числе и в функцию.
Имеем:
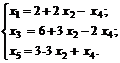
F = -2 - x2 + x4.
Базисное решение, соответствующее базису Б2{x1, x3, x5}, имеет вид (2, 0, 6, 0, 3), и функция принимает значение F= -2 в этом базисе.
Значение функции можно и дальше уменьшать, увеличивая x2. Однако, глядя на систему, x2 можно увеличивать лишь до 1, т. к. иначе из последнего равенства x5 = 3 - 3x2 + x4 следует, что при x2 > 1 x5 станет отрицательной. А у нас все переменные в ЗЛП предполагаются неотрицательными. Остальные уравнения системы не дают ограничений на x2. Поэтому увеличим x2 до 1, введя его в базис вместо x5: Б3{x1, x2, x3}.
Выразим x2 через x5 и подставим во все уравнения:
![]()
![]()
![]()
![]()
Базисное решение, соответствующее базису Б3{х1, х2,х3}, выписывается (4, 1, 9, 0, 0), и функция принимает значение F= -3. Заметим, что значение F уменьшилось, т. е. улучшилось по сравнению с предыдущим базисом.
Посмотрев на вид целевой функции ![]() , заметим, что улучшить, т. е. уменьшить значение F нельзя и только при x4 = 0, x5 = 0 значение F= -3. как только x4, x5 станут положительными, значение F только увеличится, т. к. коэффициенты при x4, x5 положительны. Значит, функция F достигла своего оптимального значения F* = -3. Итак, наименьшее значение F, равное -3, достигается при x1* = 4, x2* = 1, x3* = 9, x4* = 0, x5* = 0.
, заметим, что улучшить, т. е. уменьшить значение F нельзя и только при x4 = 0, x5 = 0 значение F= -3. как только x4, x5 станут положительными, значение F только увеличится, т. к. коэффициенты при x4, x5 положительны. Значит, функция F достигла своего оптимального значения F* = -3. Итак, наименьшее значение F, равное -3, достигается при x1* = 4, x2* = 1, x3* = 9, x4* = 0, x5* = 0.
На этом примере очень наглядно продемонстрирована идея метода: постепенно переходя от базиса к базису, при этом всегда обращая внимание на значения целевой функции, которые должны улучшиться, мы приходим к такому базису, в котором значение целевой функции улучшить нельзя, оно оптимально. Заметим, что базисов конечное число, поэтому количество шагов, совершаемых нами до того нужного базиса, конечно.