Решение транспортную задачу распределительным методом
Типовые задания транспортных задач для решения калькулятором.12.1. В пунктах А и В находятся соответственно 150 т. и 90 т. горючего. Пунктам 1, 2, 3 требуется соответственно 60, 70, 110 т. Горючего. Стоимость перевозки 1т. Горючего из пункта А в пункты 1, 2, 3 равна 60, 10, 40 тыс. руб. за 1 т. соответственно, а из пункта В в пункты 1, 2, 3 – 120, 20, 80 тыс. руб. за 1 т. соответственно. Составьте план перевозок горючего, минимизирующий общую сумму транспортных расходов.
12.2. В угольном бассейне добывается уголь, который хранится на трех складах в количестве 120, 60, 100 ед. соответственно. Добытый уголь доставляется четырем энергетическим установкам в количестве 70, 90, 50, и 70 ед. Стоимость доставки 1 ед. угля из каждого склада соответствующим энергетическим установкам задана матрицей 
. Определить оптимальный план доставки угля энергетическим установкам, обеспечивающий суммарные минимальные затраты.
12.3. Три завода выпускают комбайны, которые отправляются потребителям. Первый завод поставляет 50 комбайнов, второй – 40 комбайнов, третий – 70 комбайнов. Каждому из потребителей требуется соответственно 30, 50, 40 и 40 комбайнов. Стоимость перевозки одной единицы техники от поставщика потребителю задана матрицей стоимостей 
. Составьте оптимальный план, обеспечивающий общую минимальную стоимость перевозки комбайнов.
12.4. На двух складах А и В находится по 90 т. горючего. Перевозка одной тонны горючего со склада А в пункты 1, 2, 3 соответственно стоит 1, 3 и 5 д.е., а перевозка одной тонны со склада В в те же пункты – соответственно 2, 5 и 4 д.е. В каждый пункт надо доставить по одинаковому количеству тонн горючего. Составить такой план перевозки горючего, при котором транспортные расходы будут наименьшими.
12.5. В резерве трех железнодорожных станций А, В, С находятся соответственно 60, 80, 100 вагонов. Составить оптимальный план перегона этих вагонов к четырем пунктам погрузки хлеба, если пункту 1 необходимо 40 вагонов, пункту 2 – 60 вагонов, пункту 3 – 80 вагонов и пункту 4 – 60 вагонов. Стоимости перегонов одного вагона со станции А в указанные пункты соответственно равны 1, 2, 3, 4 д.е., со станции В – 4, 3, 2 и 1 д.е., со станции С – 1, 2, 2, 1 д.е.
12.6. Завод имеет три цеха А, В, С и четыре склада.1, 2, 3, и 4. Цех А производит 30 тыс. шт. изделий, цех В – 40 тыс. шт., цех С – 20 тыс. шт. Пропускная способность складов за то же время характеризуется следующими показателями: склад 1 – 20 тыс. шт., склад 2 – 30 тыс. шт., склад 3 – 30 тыс. шт., склад 4 – 10 тыс. шт. Стоимости перевозки 1 тыс. шт. изделий из цеха А в склады 1, 2, 3, 4 соответственно равны 2, 3, 2, 4 д.е., из цеха В – 3, 2, 5, 1 д.е., из цеха С – 4, 3, 2, 6 д.е. Составить такой план перевозки изделий, при котором расходы на перевозку 90 тыс. шт. изделий были бы минимальными.
12.7. На трех автобазах имеются автобусы в количестве 35, 45, 50 шт. соответственно для обслуживания четырех маршрутов. Для перевозки пассажиров каждому из маршрутов требуется автобусов в количестве 40,25, 35 и 30 шт. соответственно. Расходы по эксплуатации каждой транспортной единицы заданы матрицей 
. Распределить имеющиеся транспортные средства (автобусы) по маршрутам таким образом, чтобы общие расходы были минимальными.
12.8. Три завода выпускают грузовые автомобили, которые отправляются четырем потребителям. Первый завод поставляет 90 платформ грузовиков, второй – 30 платформ, третий – 40 платформ. Требуется поставить платформы следующим потребителям: первому – 70 шт., второму – 30 шт., третьему – 20 шт., четвертому – 40 шт. Стоимость перевозки одной платформы от поставщика до потребителя указана в следующей таблице (д.е.):
Поставщики | Потребители | |||
I |
II | III |
IV | |
1 2 3 | 18 10 16 | 20 20 22 | 14 40 10 | 10 30 20 |
Составьте оптимальный план доставки грузовых автомобилей, обеспечивающий минимальные расходы.
12.9. На складах А, В, С находится сортовое зерно 100, 150, 250 т., которое нужно доставить в четыре пункта. Пункту 1 необходимо поставить 50 т., пункту 2 – 100 т., пункту 3 – 200 т., пункту 4 – 150 т. сортового зерна. Стоимость доставки 1 т. зерна со склада А в указанные пункты соответственно равна (д. е.) 80, 30, 50, 20; со склада В – 40, 10, 60, 70; со склада С – 10, 90, 40, 30. Составьте оптимальный план перевозки зерна из условия минимума стоимости перевозки.
12.10. Груз, находящийся на трех складах и требующий для перевозки 60, 80, 106 автомашин соответственно, необходимо перевезти в четыре магазина, Первому магазину требуется 44 машины груза, второму – 70, третьему- 50 и четвертому – 82 машины. Стоимость пробега одной автомашины за 1 км составляет 10 д.е. Расстояния от складов до магазинов указаны в таблице:
Склады | Машины | |||
1 |
2 | 3 |
4 | |
1 2 3 | 18 2 12 | 17 7 18 | 6 10 2 | 8 41 22 |
Составьте оптимальный по стоимости план перевозки груза от складов до магазинов.
12.11. Имеются два хранилища с однородным продуктом, в которых сосредоточено 200 и 120 т. продукта соответственно. Продукты необходимо перевезти трем потребителям соответственно в количестве 80, 100 и 120 т. Расстояния (в км) от хранилищ до потребителей заданы в таблице:
Хранилище | Потребители | ||
1 |
2 | 3 | |
1 2 | 20 60 | 30 20 | 50 40 |
Затраты на перевозку 1 т. продукта на 1 км постоянны и равны 5 д.е.Определите план перевозок продукта от хранилищ до потребителей из условия минимизации транспортных расходов.
Примечание:предварительно необходимо умножить данные таблицы на 5. Далее решается стандартно через сервис.
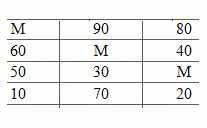
12.12. На трех складах оптовой базы находится товар в количествах, равных соответственно 140, 300 и 180 т. Этот товар необходимо завезти в пять магазинов, каждый из которых должен получить соответственно 90, 120, 230, 180 и 60 т. С первого склада товар не предоставляется возможным перевозить во второй и пятый магазины, а из второго склада в третий магазин было завезено 100 т. товара. Зная стоимости перевозки 1 т. товара с каждого из складов в соответствующие магазины, которые определяются матрицей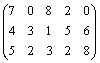 
, составьте план перевозок, обеспечивающий минимальную общую стоимость перевозок.
12.13. Строительный песок добывается в трех карьерах и доставляется на четыре строительные площадки. Производительность карьеров за день составляет соответственно 45 т, 35 т, 40 т., Потребности в песке строительных площадок составляют соответственно 30 т, 40 т, 50 т. Транспортные расходы определены матрицей 
. Определить план закрепления строительных площадок за карьерами. Обеспечивающий минимальные расходы.
12.14. Продукция выпускается на трех заводах в количестве 340, 300, 460. Спрос на эту продукцию определяется соответственно в количестве 350, 200, 450 и 100. Транспортные расходы на доставку 1 ед. продукции с i-го завода (i = 1, 2, 3) k-му потребителю (k = 1, 2, 3, 4) определены матрицей 
. Определить оптимальный план прикрепления потребителей к заводам из условия минимизации затрат на транспортировку.
12.15. На трех железнодорожных станциях А, В, С скопилось 120, 110 и 130 незагруженных вагонов. Эти вагоны необходимо перегнать на железнодорожные станции 1, 2, 3, 4 и 5. На каждой из этих станций потребность в вагонах равна соответственно 80, 60, 70, 100 и 50. Учитывая, что с железнодорожной станции В не предоставляется возможным перегнать вагоны на станции 2 и 4, и зная, что тарифы перегонки одного вагона определяются матрицей 
, составьте такой план перегонов вагонов, чтобы общая стоимость была минимальной.
12.16. Груз доставляется в пункты 1, 2, 3, и 4 в количестве 30, 40, 50 и 60 единиц со складов А, В, С и Е, в которых находился данный груз в количестве 20, 40, 50 и 70 единиц. Стоимость перевозки единицы груза от каждого поставщика каждому потребителю задана матрицей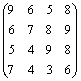 
. Требуется составить такой план перевозок, при котором общая стоимость перевозки груза минимальна.
12.17. Имеются четыре хранилища с однородным продуктом, в которых сосредоточено 200 т, 120 т, 150 т, 130 т продукта соответственно Продукты необходимо перевезти трем потребителям соответственно в количестве 200 т, 250 т, 150 т. Расстояния от хранилищ до потребителей (в км) заданы в таблице:
Хранилище | Потребители | ||
1 |
2 | 3 | |
1 2 3 4 | 20 50 60 30 | 30 20 40 30 | 50 40 30 60 |
Затраты на перевозку 1 т продукта на 1 км постоянны и равны 5 д.е. Определить план перевозок продукта от хранилищ до потребителей из условия минимизации транспортных расходов.
12.18. промышленный концерн имеет два завода и пять складов в различных регионах страны. Каждый месяц первый завод производит 40 ед. продукции, а второй – 70 ед. продукции. Вся продукция, произведенная заводами, должна быть направлена на склады. Вместимость первого склада равна 20 ед. продукции, второго – 30, третьего – 15, четвертого – 27, пятого – 28 ед. продукции. Издержки транспортировки продукции от завода до склада заданы матрицей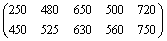 
. Распределите план перевозок из условия минимизации ежемесячных расходов на транспортировку.
12.19. Три нефтеперерабатывающих завода с суточной производительностью 10, 8, 7 млн галлонов бензина снабжают четыре бензохранилища, спрос которых составляет 6, 7, 8 и 5 млн галлонов. Бензин транспортируется в бензохранилища по трубопроводу. Стоимость перекачки бензина на 1 км составляет 5 д.е. на 100 галлонов. Завод 1 не связан с хранилищем 3. Расстояние от заводов до бензохранилищ заданы матрицей 
. Распределите план перевозок из условия минимизации транспортных затрат.
12.20. На четырех складах находится соответственно 150, 100, 90 и 110 т горючего. Пунктам 1, 2, 3 требуется соответственно 160, 110, 180 т горючего. Стоимость перевозки 1 т горючего с i-го склада (i = 1, 2, 3, 4) в k-й пункт (k = 1, 2, 3) задана матрицей стоимостей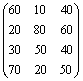 
. Составьте план перевозок горючего, минимизирующий общую стоимость транспортных расходов.
12.21. Автомобили перевозятся на трайлерах из трех центров четырем продавцам в количестве 50, 60, 80 и 50 шт. соответственно. В каждом из трех центров находилось соответственно 90, 100 и 50 шт. автомобилей. Стоимость перевозки одной единицы транспортного средства задана матрицей 
. Найдите минимальные суммарные затраты на перевозку автомобилей.
12.22. Овощи, хранящиеся на четырех складах в количестве 50, 60, 45 и 65 т соответственно, необходимо вывезти трем магазинам. Каждый магазин должен получить овощи в количестве 100, 80 и 40 т соответственно. Со второго склада овощи не вывозятся в третий магазин, а с четвертого склада – во второй. Стоимость перевозки 1т овощей с каждого из складов в соответствующие магазины задана матрицей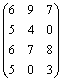 
. Составьте план перевозок, обеспечивающий минимальную общую стоимость перевозок.
12.23. В резерве трех железнодорожных станций А, В, С находятся соответственно 100, 80, 120 вагонов. Составить оптимальный план перегона этих вагонов к четырем пунктам погрузки товара, если пункту 1 необходимо 90 вагонов, пункту 2 – 80 вагонов, пункту 3 – 70 вагонов и пункту 4 – 60 вагонов. Стоимости перегонов одного вагона со станции А в указанные пункты соответственно равны 4, 5, 3, 4 д.е., со станции В – 1, 3, 5 и 1 д.е., со станции С – 6, 2, 7, 1 д.е.
12.24. В угольном бассейне добывается уголь трех сортов в относительных долях 20%, 60%, 15%. Добытый уголь доставляется четырем энергетическим установкам. Заданы теплотворные способности каждого из сортов топлива (в ккал/кг): 2800; 3000; 3500, потребности установок (в млн. ккал): 10; 25; 15; 30 и затраты по добыче 1 т. каждого сорта (в руб.): 8, 10, 15. Определить требуемый объем добычи и распределение разных сортов угля между энергетическими установками из условия минимизации суммарных затрат.
12.25. На строительном полигоне имеются два кирпичных завода, объем производства которых в сутки равен 600 и 700 т. Заводы удовлетворяют потребности пяти строительных объектов соответственно в количестве 250, 300, 150, 200 и 400 т. Кирпич на строительные объекты доставляется автотранспортом. Стоимость перевозки 1 т. кирпича с каждого из заводов соответствующим строительным полигонам указана в матрице стоимостей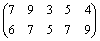 
. Определить план перевозки кирпича строительным полигонам, обеспечивающий минимальную стоимость перевозки.
12.26. На трех складах оптовой базы сосредоточен однородный груз в количествах 90, 60 и 150 ед. Этот груз необходимо перевезти в четыре магазина. Каждый из магазинов должен получить соответственно 120, 40, 60 и 80 ед. груза. Тарифы перевозок единицы груза из каждого из складов во все магазины задаются матрицей 
.
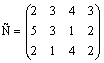Составить такой план перевозок, при котором общая стоимость является минимальной.
12.27. Производственное объединение имеет в своем составе три филиала, которые производят однородную продукцию соответственно в количествах, равных 50, 30 и 10 ед. Эту продукцию получают четыре потребителя, расположенные в разных местах. Их потребности соответственно равны 30, 30, 10 и 20 ед. Тарифы перевозок единицы продукции от каждого из филиалов соответствующим потребителям задаются матрицей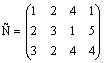 
.
Составить такой план прикрепления получателей продукции к ее поставщикам, при котором общая стоимость перевозок является минимальной.
12.28. Три предприятия данного экономического района могут производить некоторую однородную продукцию в количествах, соответственно равных 180, 350 и 20 ед. Эта продукция должна быть поставлена пяти потребителям в количествах, соответственно равных 110, 90, 120, 80 и 150 ед. Затраты, связанные с производством и доставкой единицы продукции, задаются матрицей 
.
Составить такой план прикрепления потребителей к поставщикам, при котором общие затраты являются минимальными.
12.29. На трех хлебокомбинатах ежедневно производится 110, 190 и 90 т муки. Эта мука потребляется четырьмя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 т. Тарифы перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов задаются матрицей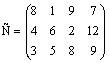 
.
Составить такой план доставки муки, при котором общая стоимость перевозок является минимальной.
12.30. В трех хранилищах горючего ежедневно хранится 175, 125 и 140 т бензина. Этот бензин ежедневно получают четыре заправочные станции в количествах, равных соответственно 180, 110, 90 и 40 т. Тарифы перевозок 1 т бензина с хранилищ к заправочным станциям задаются матрицей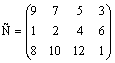 
.
Составит такой план перевозок бензина, при котором общая стоимость перевозок является минимальной.
см. решение.
Перейти к онлайн решению своей задачи
Пример. Решить ТЗ распределительным методом.
Распределительный метод заключается в нахождении оценок циклов пересчета для всех свободных клеток транспортной таблицы. Если оценка цикла отрицательна, то решение задачи можно улучшить путем переноса перевозки xij по циклу. Если оценки для всех циклов неотрицательны, то решение оптимально.
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
Распределительный метод является одним из вариантов базового симплексного метода. Поэтому идея распределительного метода (как и симплексного) содержит такие же три существенных момента.
Прежде всего отыскивается какое-то решение задачи — исходный опорный план. Затем посредством специальных показателей опорный план проверяется на оптимальность. Если план оказывается не оптимальным, переходят к другому плану. При этом второй и последующие планы должны быть лучше предыдущего. Так за несколько последовательных переходов от не оптимального плана приходят к оптимальному.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3 | 5 | 80 |
| 2 | 5 | 4 | 4 | 3 | 105 |
| 3 | 6 | 5 | 6 | 4 | 125 |
| 4 | 8 | 4 | 2 | 4 | 90 |
| Потребности | 110 | 130 | 160 | 120 |
Проверим необходимое и достаточное условие разрешимости задачи.
∑ a = 80 + 105 + 125 + 90 = 400
∑ b = 110 + 130 + 160 + 120 = 520
Как видно, суммарная потребность груза в пунктах назначения меньше запасов груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) потребность, равным 120 (520—400). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.
Занесем исходные данные в распределительную таблицу.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3 | 5 | 80 |
| 2 | 5 | 4 | 4 | 3 | 105 |
| 3 | 6 | 5 | 6 | 4 | 125 |
| 4 | 8 | 4 | 2 | 4 | 90 |
| 5 | 0 | 0 | 120 | ||
| Потребности | 110 | 130 | 160 | 120 |
Первая итерация заключается в определении исходного опорного плана и проверке его на оптимальность.
Определение исходного опорного плана. Первый опорный план может быть найден посредством различных способов: по правилу северо-западного угла, приоритету ближайших пунктов, способу минимального элемента С=(cij), способу Фогеля и по способу Лебедева-Тихомирова.
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10] | 6 | 3[70] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100] | 0[20] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.
2. Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 8. Следовательно, опорный план является невырожденным.
Значение целевой функции для этого опорного плана равно:
F(x) = 6*10 + 3*70 + 3*105 + 5*110 + 4*15 + 2*90 + 0*100 + 0*20 = 1375
Проверка опорного плана на оптимальность.Чтобы установить является ли опорный план оптимальным, надо проверить, как повлияет на величину целевой функции любое возможное перераспределение поставок.
План распределения поставок будет оптимальным лишь в том случае, когда целевая функция имеет минимальное значение, т.е. когда дальнейшее уменьшение затрат на поставку будет невозможно.
Проверим возможность уменьшения суммарных затрат на поставку продукции. С этой целью для каждой свободной от поставки клетки определяется величина Δij, характеризующая изменение суммарных затрат на поставку (в расчете на единицу перераспределяемой продукции), при условии включения в план единичной поставки хij=1 от поставщика Аiк потребителю Вj.
При этом должно быть произведено такое изменение остальных поставок, чтобы получившаяся совокупность поставок не нарушала баланса спроса и поставок транспортной задачи.
Величина Δijназывается оценкой свободной клетки(или характеристика).
В исходном решении задачи имеются клетки свободные от поставок.
Необходимо вычислить значение оценок Δijдля этих свободных от поставок клеток. С этой целью для каждой свободной клетки составляется означенный цикл перерасчета (или замкнутая цепь, круг, кольцо, контур и т.д.).
Под циклом пересчета (цепью)понимается замкнутая ломаная линия. Вершинами цикла (цепи) являются клетки таблицы, проще – вершины лежат в клетках таблицы.
Причем одна из вершин находится в свободной от поставки клетке, в той, для которой определяется оценка Δij. Все другие вершины находятся в базисных клетках, т.е. клетках, занятых поставками.
Вершины, в которых поставки при перераспределении увеличиваются, отмечаются плюсом и называются положительными вершинами и, наоборот, вершины, в которых поставки при перераспределении уменьшаются отмечаются минусом и называются отрицательными вершинами.
В цикле знаки по вершинам расставляют начиная с вершины, лежащей в свободной клетке, для которой определяется Δij. В нее записывают знак плюс, затем знаки по вершинам чередуются: минус, плюс , минус, плюс и т. д., независимо от того, расставляют ли их по часовой стрелке или в обратном направлении. Таким образом, в цикле всегда насчитывается одинаковое число положительных и отрицательных вершин.
Следующий этап решения транспортной задачи заключается в улучшении опорного плана.
Если при каком-то опорном плане оказывается несколько свободных клеток с отрицательными оценками Δij, то за один переход к лучшему плану можно занять поставкой только одну клетку – ту, которая обеспечивает наибольшее снижение целевой функции.
4. Определяем оценку для каждой свободной клетки.
В свободную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][-] | 6[+] | 3[70] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100][+] | 0[20][-] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (1,2; 1,1; 5,1; 5,2; ).
Оценка свободной клетки равна Δ12= (6) - (6) + (0) - (0) = 0
В свободную клетку (1;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][-] | 6 | 3[70] | 5[+] | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110][+] | 6 | 4[15][-] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100][+] | 0[20][-] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (1,4; 1,1; 5,1; 5,2; 3,2; 3,4; ).
Оценка свободной клетки равна Δ14= (5) - (6) + (0) - (0) + (5) - (4) = 0
В свободную клетку (2;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10] | 6 | 3[70] | 5 | 80 |
| 2 | 5[+] | 4 | 4 | 3[105][-] | 105 |
| 3 | 6 | 5[110][-] | 6 | 4[15][+] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100][-] | 0[20][+] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (2,1; 2,4; 3,4; 3,2; 5,2; 5,1; ).
Оценка свободной клетки равна Δ21= (5) - (3) + (4) - (5) + (0) - (0) = 1
В свободную клетку (2;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10] | 6 | 3[70] | 5 | 80 |
| 2 | 5 | 4[+] | 4 | 3[105][-] | 105 |
| 3 | 6 | 5[110][-] | 6 | 4[15][+] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100] | 0[20] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (2,2; 2,4; 3,4; 3,2; ).
Оценка свободной клетки равна Δ22= (4) - (3) + (4) - (5) = 0
В свободную клетку (2;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][+] | 6 | 3[70][-] | 5 | 80 |
| 2 | 5 | 4 | 4[+] | 3[105][-] | 105 |
| 3 | 6 | 5[110][-] | 6 | 4[15][+] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100][-] | 0[20][+] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (2,3; 2,4; 3,4; 3,2; 5,2; 5,1; 1,1; 1,3; ).
Оценка свободной клетки равна Δ23= (4) - (3) + (4) - (5) + (0) - (0) + (6) - (3) = 3
В свободную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10] | 6 | 3[70] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6[+] | 5[110][-] | 6 | 4[15] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100][-] | 0[20][+] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (3,1; 3,2; 5,2; 5,1; ).
Оценка свободной клетки равна Δ31= (6) - (5) + (0) - (0) = 1
В свободную клетку (3;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][+] | 6 | 3[70][-] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110][-] | 6[+] | 4[15] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100][-] | 0[20][+] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (3,3; 3,2; 5,2; 5,1; 1,1; 1,3; ).
Оценка свободной клетки равна Δ33= (6) - (5) + (0) - (0) + (6) - (3) = 4
В свободную клетку (4;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][-] | 6 | 3[70][+] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8[+] | 4 | 2[90][-] | 4 | 90 |
| 5 | 0[100] | 0[20] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (4,1; 4,3; 1,3; 1,1; ).
Оценка свободной клетки равна Δ41= (8) - (2) + (3) - (6) = 3
В свободную клетку (4;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][-] | 6 | 3[70][+] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8 | 4[+] | 2[90][-] | 4 | 90 |
| 5 | 0[100][+] | 0[20][-] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (4,2; 4,3; 1,3; 1,1; 5,1; 5,2; ).
Оценка свободной клетки равна Δ42= (4) - (2) + (3) - (6) + (0) - (0) = -1
В свободную клетку (4;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][-] | 6 | 3[70][+] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110][+] | 6 | 4[15][-] | 125 |
| 4 | 8 | 4 | 2[90][-] | 4[+] | 90 |
| 5 | 0[100][+] | 0[20][-] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (4,4; 4,3; 1,3; 1,1; 5,1; 5,2; 3,2; 3,4; ).
Оценка свободной клетки равна Δ44= (4) - (2) + (3) - (6) + (0) - (0) + (5) - (4) = 0
В свободную клетку (5;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][+] | 6 | 3[70][-] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100][-] | 0[20] | 0[+] | 0 | 120 |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (5,3; 5,1; 1,1; 1,3; ).
Оценка свободной клетки равна Δ53= (0) - (0) + (6) - (3) = 3
В свободную клетку (5;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10] | 6 | 3[70] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110][+] | 6 | 4[15][-] | 125 |
| 4 | 8 | 4 | 2[90] | 4 | 90 |
| 5 | 0[100] | 0[20][-] | 0[+] | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (5,4; 5,2; 3,2; 3,4; ).
Оценка свободной клетки равна Δ54= (0) - (0) + (5) - (4) = 1
Опорный план является неоптимальным, поскольку имеются отрицательны оценки клеток (4,2;) равные: (-1).
Переход от неоптимального опорного плана к лучшему.
Поскольку в исходном опорном плане рассматриваемой задачи свободная клетка (4;2) имеет отрицательную оценку, то для получения плана, обеспечивающего меньшее значение целевой функции, эту клетку следует занять возможно большей поставкой, не нарушающей при этом условий допустимости плана.
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 1) = 10. Прибавляем 10 к объемам грузов, стоящих в плюсовых клетках и вычитаем 10 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8 | 4[10] | 2[80] | 4 | 90 |
| 5 | 0[110] | 0[10] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
F(x) = 3*80 + 3*105 + 5*110 + 4*15 + 4*10 + 2*80 + 0*110 + 0*10 = 1365
4. Определяем оценку для каждой свободной клетки.
В свободную клетку (1;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[+] | 6 | 3[80][-] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8 | 4[10][-] | 2[80][+] | 4 | 90 |
| 5 | 0[110][-] | 0[10][+] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (1,1; 1,3; 4,3; 4,2; 5,2; 5,1; ).
Оценка свободной клетки равна Δ11= (6) - (3) + (2) - (4) + (0) - (0) = 1
В свободную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6[+] | 3[80][-] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8 | 4[10][-] | 2[80][+] | 4 | 90 |
| 5 | 0[110] | 0[10] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (1,2; 1,3; 4,3; 4,2; ).
Оценка свободной клетки равна Δ12= (6) - (3) + (2) - (4) = 1
В свободную клетку (1;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80][-] | 5[+] | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110][+] | 6 | 4[15][-] | 125 |
| 4 | 8 | 4[10][-] | 2[80][+] | 4 | 90 |
| 5 | 0[110] | 0[10] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (1,4; 1,3; 4,3; 4,2; 3,2; 3,4; ).
Оценка свободной клетки равна Δ14= (5) - (3) + (2) - (4) + (5) - (4) = 1
В свободную клетку (2;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5[+] | 4 | 4 | 3[105][-] | 105 |
| 3 | 6 | 5[110][-] | 6 | 4[15][+] | 125 |
| 4 | 8 | 4[10] | 2[80] | 4 | 90 |
| 5 | 0[110][-] | 0[10][+] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (2,1; 2,4; 3,4; 3,2; 5,2; 5,1; ).
Оценка свободной клетки равна Δ21= (5) - (3) + (4) - (5) + (0) - (0) = 1
В свободную клетку (2;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4[+] | 4 | 3[105][-] | 105 |
| 3 | 6 | 5[110][-] | 6 | 4[15][+] | 125 |
| 4 | 8 | 4[10] | 2[80] | 4 | 90 |
| 5 | 0[110] | 0[10] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (2,2; 2,4; 3,4; 3,2; ).
Оценка свободной клетки равна Δ22= (4) - (3) + (4) - (5) = 0
В свободную клетку (2;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4 | 4[+] | 3[105][-] | 105 |
| 3 | 6 | 5[110][-] | 6 | 4[15][+] | 125 |
| 4 | 8 | 4[10][+] | 2[80][-] | 4 | 90 |
| 5 | 0[110] | 0[10] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (2,3; 2,4; 3,4; 3,2; 4,2; 4,3; ).
Оценка свободной клетки равна Δ23= (4) - (3) + (4) - (5) + (4) - (2) = 2
В свободную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6[+] | 5[110][-] | 6 | 4[15] | 125 |
| 4 | 8 | 4[10] | 2[80] | 4 | 90 |
| 5 | 0[110][-] | 0[10][+] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (3,1; 3,2; 5,2; 5,1; ).
Оценка свободной клетки равна Δ31= (6) - (5) + (0) - (0) = 1
В свободную клетку (3;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110][-] | 6[+] | 4[15] | 125 |
| 4 | 8 | 4[10][+] | 2[80][-] | 4 | 90 |
| 5 | 0[110] | 0[10] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (3,3; 3,2; 4,2; 4,3; ).
Оценка свободной клетки равна Δ33= (6) - (5) + (4) - (2) = 3
В свободную клетку (4;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8[+] | 4[10][-] | 2[80] | 4 | 90 |
| 5 | 0[110][-] | 0[10][+] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (4,1; 4,2; 5,2; 5,1; ).
Оценка свободной клетки равна Δ41= (8) - (4) + (0) - (0) = 4
В свободную клетку (4;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110][+] | 6 | 4[15][-] | 125 |
| 4 | 8 | 4[10][-] | 2[80] | 4[+] | 90 |
| 5 | 0[110] | 0[10] | 0 | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (4,4; 4,2; 3,2; 3,4; ).
Оценка свободной клетки равна Δ44= (4) - (4) + (5) - (4) = 1
В свободную клетку (5;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110] | 6 | 4[15] | 125 |
| 4 | 8 | 4[10][+] | 2[80][-] | 4 | 90 |
| 5 | 0[110] | 0[10][-] | 0[+] | 0 | 120 |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (5,3; 5,2; 4,2; 4,3; ).
Оценка свободной клетки равна Δ53= (0) - (0) + (4) - (2) = 2
В свободную клетку (5;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 6 | 3[80] | 5 | 80 |
| 2 | 5 | 4 | 4 | 3[105] | 105 |
| 3 | 6 | 5[110][+] | 6 | 4[15][-] | 125 |
| 4 | 8 | 4[10] | 2[80] | 4 | 90 |
| 5 | 0[110] | 0[10][-] | 0[+] | 120 | |
| Потребности | 110 | 130 | 160 | 120 |
Цикл приведен в таблице (5,4; 5,2; 3,2; 3,4; ).
Оценка свободной клетки равна Δ54= (0) - (0) + (5) - (4) = 1
Из приведенного расчета видно, что ни одна свободная клетка не имеет отрицательной оценки, следовательно, дальнейшее снижение целевой функции Fx невозможно, поскольку она достигла минимального значения.
Таким образом, последний опорный план является оптимальным.
Минимальные затраты составят: F(x) = 3*80 + 3*105 + 5*110 + 4*15 + 4*10 + 2*80 + 0*110 + 0*10 = 1365
Если в оптимальном решении задачи имеется несколько оценок равных нулю, то это является свидетельством того, что среди бесчисленного множества решений этой задачи существуют еще решения, являющиеся также оптимальными, поскольку значение целевой функции остается одинаковым — минимальным. Их принято называть альтернативными.
Примечание. Основной алгоритм распределительного метода является не лучшим методом решения транспортных задач, так как на каждой итерации для проверки опорного плана на оптимальность приходилось строить [mп—(m+n—1)] циклов пересчета, что при больших размерах матрицы оказывается очень громоздким и трудоемким делом. Так, для расчетов по матрице 10х10 на каждой итерации надо строить 81 цикл, а по матрице 20x20 — 361 цикл.
Пример. Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов.
1 | 2 | 3 | 4 | Запасы | |
1 |
1 | 2 |
4 | 3 |
6 |
2 | 4 | 3 | 8 | 5 | 8 |
3 |
2 | 7 |
6 | 3 |
10 |
Потребности | 4 | 6 | 8 | 8 |
Решение находим с помощью онлайн сервиса Метод потенциалов. Проверим необходимое и достаточное условие разрешимости задачи.
∑ a = 6 + 8 + 10 = 24
∑ b = 4 + 6 + 8 + 8 = 26
Как видно, суммарная потребность груза в пунктах назначения меньше запасов груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) потребность, равным 2 (26—24). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.
Занесем исходные данные в распределительную таблицу.
1 | 2 | 3 | 4 | Запасы | |
1 |
1 | 2 |
4 | 3 |
6 |
2 | 4 | 3 | 8 | 5 | 8 |
3 |
2 | 7 |
6 | 3 |
10 |
4 | 0 | 0 | 0 | 0 | 2 |
Потребности |
4 | 6 |
8 | 8 |
|
Первая итерация заключается в определении исходного опорного плана и проверке его на оптимальность.
Определение исходного опорного плана. Первый опорный план может быть найден посредством различных способов: по правилу северо-западного угла, приоритету ближайших пунктов, способу минимального элемента С=(cij), способу Фогеля и по способу Лебедева-Тихомирова.
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
1 | 2 | 3 | 4 | Запасы | |
1 |
1[4] | 2[2] |
4 | 3 |
6 |
2 | 4 | 3[4] | 8[4] | 5 | 8 |
3 |
2 | 7 |
6[2] | 3[8] |
10 |
4 | 0 | 0 | 0[2] | 0 | 2 |
Потребности |
4 | 6 |
8 | 8 |
|
Пример. Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
1 | 2 | 3 | 4 | Запасы | |
1 |
5 | 4 |
3 | 2 |
190 |
2 | 4 | 7 | 4 | 4 | 200 |
3 |
3 | 5 |
6 | 8 |
160 |
4 | 4 | 3 | 7 | 5 | 100 |
Потребности |
180 | 200 |
150 | 120 |
|
Проверим необходимое и достаточное условие разрешимости задачи.
∑ a = 190 + 200 + 160 + 100 = 650
∑ b = 180 + 200 + 150 + 120 = 650
Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
Занесем исходные данные в распределительную таблицу.
1 | 2 | 3 | 4 | Запасы | |
1 |
5 | 4 |
3 | 2 |
190 |
2 | 4 | 7 | 4 | 4 | 200 |
3 |
3 | 5 |
6 | 8 |
160 |
4 | 4 | 3 | 7 | 5 | 100 |
Потребности |
180 | 200 |
150 | 120 |
|
Первая итерация заключается в определении исходного опорного плана и проверке его на оптимальность.
Определение исходного опорного плана. Первый опорный план может быть найден посредством различных способов: по правилу северо-западного угла, приоритету ближайших пунктов, способу минимального элемента С=(cij), способу Фогеля и по способу Лебедева-Тихомирова.
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
1 | 2 | 3 | 4 | Запасы | |
1 |
5 | 4 |
3[70] | 2[120] |
190 |
2 | 4[20] | 7[100] | 4[80] | 4 | 200 |
3 |
3[160] | 5 |
6 | 8 |
160 |
4 | 4 | 3[100] | 7 | 5 | 100 |
Потребности |
180 | 200 |
150 | 120 |
|
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным.
Значение целевой функции для этого опорного плана равно:
F(x) = 3*70 + 2*120 + 4*20 + 7*100 + 4*80 + 3*160 + 3*100 = 2330
4. Определяем оценку для каждой свободной клетки.
В свободную клетку (1;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
1 | 2 | 3 | 4 | Запасы | |
1 |
5[+] | 4 |
3[70][-] | 2[120] |
190 |
2 | 4[20][-] | 7[100] | 4[80][+] | 4 | 200 |
3 |
3[160] | 5 |
6 | 8 |
160 |
4 | 4 | 3[100] | 7 | 5 | 100 |
Потребности |
180 | 200 |
150 | 120 |
|
Цикл приведен в таблице (1,1; 1,3; 2,3; 2,1; ).
Оценка свободной клетки равна Δ11= (5) - (3) + (4) - (4) = 2
В свободную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
1 | 2 | 3 | 4 | Запасы | |
1 |
5 | 4[+] |
3[70][-] | 2[120] |
190 |
2 | 4[20] | 7[100][-] | 4[80][+] | 4 | 200 |
3 |
3[160] | 5 |
6 | 8 |
160 |
4 | 4 | 3[100] | 7 | 5 | 100 |
Потребности |
180 | 200 |
150 | 120 |
|