Задача о назначениях
Рассмотрим ситуацию, когда требуется распределить m работ (или исполнителей) по n станкам. Работа i (i=1,...,m), выполняемая на станке j (j=1,...,n), связана с затратами cij. Задача состоит в таком распределении работ по станкам (одна работа выполняется на одном станке), которое соответствует минимизации суммарных затрат.Эту задачу можно рассматривать как частный случай транспортной задачи. Здесь работы представляют «исходные пункты», а станки – «пункты назначения». Предложение в каждом исходном пункте равно 1, т.е. ai = 1 для всех i. Аналогично спрос в каждом пункте назначения равен 1, т.е. bj = 1 для всех j. Стоимость «перевозки» (прикрепления) работы i к станку j равна cij. Если какую-либо работу нельзя выполнять на некотором станке, то соответствующая стоимость берется равной очень большому числу. Матрица стоимостей C определяется следующим образом:
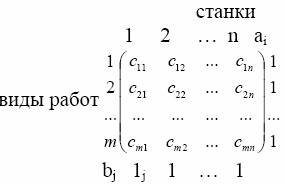
Прежде чем решать такую задачу необходимо ликвидировать дисбаланс, добавив фиктивные работы или станки в зависимости от начальных условий. Поэтому без потери общности можно положить m = n.
Пусть
xij = 0, если j-я работа не выполняется на i-м станке,
xij = 1, если j-я работа выполняется на i-м станке.
Таким образом, решение задачи может быть записано в виде двумерного массива X = (xij). Допустимое решение называется назначением. Допустимое решение строится путем выбора ровно одного элемента в каждой строке матрицы X = (xij) и ровно одного элемента в каждом столбце этой матрицы. Для заданного значения n существует n! допустимых решений.
Теперь задача будет формулироваться следующим образом:
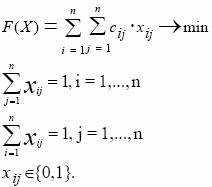
Ограничения первой группы необходимы для того, чтобы каждая работа выполнялась ровно один раз. Ограничения второй группы гарантируют, что каждому станку будет приписана ровно одна работа.
Венгерский алгоритм
Шаг 1. (Редукция строк и столбцов).
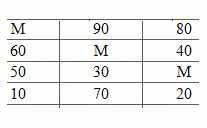
Цель данного шага состоит в получении максимально возможного числа нулевых элементов в матрице стоимостей. Для этого из всех элементов каждой строки вычитают минимальный элемент соответствующей строки, а затем из всех элементов каждого столбца полученной матрицы вычитают минимальный элемент соответствующего столбца. В результате получают редуцированную матрицу стоимостей и переходят к поиску назначений.
Шаг 2. (Определение назначений).
а) Найти строки, содержащие ровно один невычеркнутый нулевой элемент. В каждой такой строке произвести назначение, соответствующее невычеркнутому нулевому элементу. В каждом столбце, в котором было произведено назначение,
вычеркнуть все невычеркнутые ранее нулевые элементы. Строки рассматриваются в порядке возрастания их номеров.
б) Найти столбцы, содержащие ровно один невычеркнутый нулевой элемент. В каждом таком столбце произвести назначение, соответствующее невычеркнутому нулевому элементу. В каждой строке, в которой было произведено назначение, вычеркнуть все невычеркнутые ранее нулевые элементы. Столбцы рассматриваются в порядке возрастания их номеров.
в) Выполнять пункты а) и б) до тех пор, пока не будет вычеркнуто максимально возможное число нулевых элементов. Если построенное назначение полное, то оно является оптимальным.
Если некоторые нули остались невычеркнутыми, то можно попытаться найти полное назначение.
Если нельзя найти полного назначения, то необходима дальнейшая модификация матрицы стоимостей, т.е. перейти к шагу 3.
Шаг 3. (Модификация редуцированной матрицы).
Для редуцированной матрицы стоимостей:
а) Вычислить число нулей в каждой невычеркнутой строке и каждом невычеркнутом столбце.
б) Вычеркнуть строку или столбец с максимальным числом нулей.
в) Выполнять пункты а) и б) до тех пор, пока не будут вычеркнуты все нули.
г) Из всех невычеркнутых элементов вычесть минимальный невычеркнутый элемент и прибавить его к каждому элементу, расположенному на пересечении двух линий.
Перейти к шагу 2.
Замечания.
1) Если число линий, необходимое, для того чтобы вычеркнуть нулевые элементы, равно числу строк (столбцов), то существует полное назначение.
2) Если исходная задача является задачей максимизации, то все элементы матрицы стоимостей следует умножить на (-1) и сложить их с достаточно большим числом так, чтобы матрица не содержала бы отрицательных элементов. Затем задачу следует решать как задачу минимизации.
Перейти к решению задачи о назначениях