Оптимальное исследование рынка
Группе, исследующий рынок, требуется получить данные из n различных мест. В ее распоряжении имеется n дней, и она предполагает провести по одному дню в каждом месте, проведя по аj опросов, j=1,…,n. Вероятность успешного опроса в каждом месте задается матрицей Р. Элемент матрицы рij характеризует вероятность успешного опроса в течении i-го дня в j-м месте, i=1,…,n.Определить время проведения опросов, при котором общее число опросов максимально.
Решение. Сведем данную задачу к задаче о назначениях.
Введем величину rij=pijaj, показывающую число успешных опросов в в j-м месте в течение i-го дня.
xij = 1, если в i-й день опрос проводится в j-м месте;
xij =0 , в противном случае.
Математическая модель задачи имеет следующий вид:
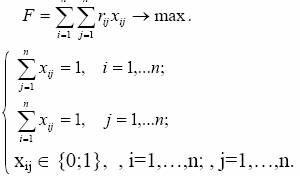
Функция F характеризует суммарное число успешных опросов. Ее нужно максимизировать. Первое и второе ограничения соответствуют тому, что в течении одного дня можно находиться только в одном месте. Для расчета модели венгерским методом надо перейти к противоположной функции:
и в соответствующей таблице записывать значения rij с противоположным знаком.
Перейти к решению транспортной задачи