Решение транспортной задачи линейного программирования
Опорное решение транспортной задачи
Опорным решением транспортной задачи называется любое допустимое решение, для которого векторы-условия, соответствующие положительным координатам, линейно независимы.Ввиду того, что ранг системы векторов условий транспортной задачи равен k + n- 1, опорное решение не может иметь отличных от нуля координат более k + n- 1. Число отличных от нуля координатневырожденного опорного решения равно k+ n- 1, а для вырожденного опорного решения меньше k + n- 1.
Любое допустимое решение транспортной задачи можно записать в ту же таблицу, что и исходные данные. Клетки таблицы транспортной задачи, в которых находятся отличные от нуля или базисные нулевые перевозки, называются занятыми, остальные — незанятыми или свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку хij т.е. стоящая в i-й строке и j-м столбце, имеет номер (i, j). Каждой клетке с номером (i, j)соответствует переменная хij, которой соответствует вектор-условиеAij.
Для того чтобы избежать трудоемких вычислений при проверке линейной независимости векторов-условий, соответствующих положительным координатам допустимого решения, вводят понятие цикла. Циклы также используются для перехода от одного опорного решения к другому.
Циклом называется такая последовательность клеток таблицы транспортной задачи (i1,j1), (i1,j2), (i2,j2), …,(ik,j 1 ), в которой две и только две соседние клетки расположены в одной строке или столбце, причем первая и последняя клетки также находятся в одной строке или столбце.
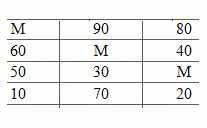
Цикл изображают в таблице транспортной задачи в виде замкнутой ломаной линии. В любой клетке цикла происходит поворот звена; ломаной линии на 90°. Простейшие циклы изображены на рисунке, где звездочкой отмечены клетки таблицы, включенные в состав цикла.
□ Теорема (о взаимосвязи линейной зависимости векторов-условий и возможности образования цикла). Для того чтобы система векторов-условий транспортной задачи была линейно зависимой, необходимо и достаточно, чтобы из соответствующих клеток таблицы можно было выделить часть, которая образует цикл.
Доказательство . Необходимость. Пусть система, состоящая из n векторов
линейно зависима. Тогда существует такой ненулевой набор чисел
Пусть λ1 ≠0. Вектор
В выбранной подобным образом последовательности векторов должен найтись вектор
Достаточность. Пусть из соответствующих векторам А ij клеток (i, j) выбрана последовательность клеток, образующих цикл (i1,j1), (i1,j2), (i2,j2),…, (i k ,j1). Нетрудно видеть, что
Отсюда следует линейная зависимость рассматриваемой системы торов. Теорема доказана полностью.
Следствие. Допустимое решение транспортной задачи X=(xij),i= 1,2, ..., k ; j= 1, 2, ..., n является опорным тогда и только тогда, когда из занятых им клеток таблицы нельзя образовать ни одного цикла.
Пример.
1. Составить допустимый план транспортной задачи, используя метод минимальной стоимости или Мюллера-Мербаха для построения базисного плана с ограничением пропускной способности.
2. Найти оптимальный план транспортной задачи, используя метод потенциалов. Построенный допустимый и оптимальный план должен удовлетворять условиям постановки транспортной задачи.
a. 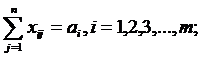
b. 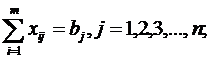
c. 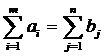
d. 0≤xij≤dij
e. Целевая функция задачи 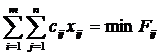
3. Рассчитать целевые функции каждого базисного плана перевозок.
4. Найти экономический эффект от оптимизации. Экономический эффект от оптимизации рассчитывается как разность между целевыми функциями базисного и оптимального планов.
5. Рассчитать матрицу показателей характеристик оптимального плана перевозок транспортной задачи. Характеристики клеток рассчитываются по формуле: Dij = cij – (vj – Uj)
6. Показать варианты альтернативных решений при одной и той же целевой функции и при минимальных от нее отклонениях.
Обсуждение
1. Составить математическую модель сбалансированной задачи линейного программирования, описав все переменные, функцию цели и ограничения.
2. Найти опорное решение сформулированной транспортной задачи методами северо-западного угла, минимального элемента и аппроксимации Фогеля. Оценить значения функции цели, полученные для каждого из опорных планов, и сделать выводы о близости этих планов к оптимальному решению.
3. Решить сформулированную выше задачу методом потенциалов и методом дифференциальных рент.
4. Проверить решение в среде Excel.
Математическая модель транспортной задачи:
F = ∑∑cijxij, (1)
при условиях:
∑xij = ai, i = 1,2,…, m, (2)
∑xij = bj, j = 1,2,…, n, (3)
С целью составления двойственной задачи переменные xij в условии (2) заменим на u1, u2, ui,.., um, а переменные xij в условия (3) на v1, v2, vj,.., vn.
Поскольку каждая переменная xij входит в условия (2,3) и целевую функцию (1) по одному разу, то двойственную задачу по отношению к прямой транспортной задаче можно сформулировать следующим образом.
Требуется найти не отрицательные числа ui (при i = 1,2,…,m) и vj (при j = 1,2,..,n), обращающие в максимум целевую функцию
G = ∑aiui + ∑bjvj
при условии
ui + vj ≤ cij, i = 1,2,..,m; j = 1,2,..,n (4)
В систему условий (4) будет mxn неравенств. По теории двойственности для оптимальных планов прямой и двойственной задачи для всех i,j должно быть:
ui + vj ≤ cij, если xij = 0,
ui + vj = cij, если xij ≥ 0,
Эти условия являются необходимыми и достаточными признаками оптимальности плана транспортной задачи.
Числа ui , vj называются потенциалами. Причем число ui называется потенциалом поставщика, а число vj – потенциалом потребителя.
По первой теореме двойственности в оптимальном решении значения целевых функций прямой и двойственных задач совпадают: F = G.
Решение
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 8 | 9 | 10 | 9 | 180 |
| 2 | 10 | 8 | 8 | 9 | 200 |
| 3 | 11 | 10 | 9 | 10 | 130 |
| 4 | 9 | 9 | 8 | 10 | 50 |
| Потребности | 60 | 80 | 220 | 100 |
∑a = 180 + 200 + 130 + 50 = 560
∑b = 60 + 80 + 220 + 100 = 460
Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 100 (560—460). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.
Занесем исходные данные в распределительную таблицу.
| 1 | 2 | 3 | 4 | 5 | Запасы | |
| 1 | 8 | 9 | 10 | 9 | 0 | 180 |
| 2 | 10 | 8 | 8 | 9 | 0 | 200 |
| 3 | 11 | 10 | 9 | 10 | 0 | 130 |
| 4 | 9 | 9 | 8 | 10 | 0 | 50 |
| Потребности | 60 | 80 | 220 | 100 | 100 |
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj.
Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.
Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Искомый элемент равен 8
Для этого элемента запасы равны 180, потребности 60. Поскольку минимальным является 60, то вычитаем его.
x11 = min(180,60) = 60.
| 8 | 9 | 10 | 9 | 0 | 180 - 60 = 120 |
| x | 8 | 8 | 9 | 0 | 200 |
| x | 10 | 9 | 10 | 0 | 130 |
| x | 9 | 8 | 10 | 0 | 50 |
| 60 - 60 = 0 | 80 | 220 | 100 | 100 | 0 |
Для этого элемента запасы равны 200, потребности 80. Поскольку минимальным является 80, то вычитаем его.
x22 = min(200,80) = 80.
| 8 | x | 10 | 9 | 0 | 120 |
| x | 8 | 8 | 9 | 0 | 200 - 80 = 120 |
| x | x | 9 | 10 | 0 | 130 |
| x | x | 8 | 10 | 0 | 50 |
| 0 | 80 - 80 = 0 | 220 | 100 | 100 | 0 |
Для этого элемента запасы равны 120, потребности 220. Поскольку минимальным является 120, то вычитаем его.
x23 = min(120,220) = 120.
| 8 | x | 10 | 9 | 0 | 120 |
| x | 8 | 8 | x | x | 120 - 120 = 0 |
| x | x | 9 | 10 | 0 | 130 |
| x | x | 8 | 10 | 0 | 50 |
| 0 | 0 | 220 - 120 = 100 | 100 | 100 | 0 |
Для этого элемента запасы равны 50, потребности 100. Поскольку минимальным является 50, то вычитаем его.
x43 = min(50,100) = 50.
| 8 | x | 10 | 9 | 0 | 120 |
| x | 8 | 8 | x | x | 0 |
| x | x | 9 | 10 | 0 | 130 |
| x | x | 8 | x | x | 50 - 50 = 0 |
| 0 | 0 | 100 - 50 = 50 | 100 | 100 | 0 |
Для этого элемента запасы равны 120, потребности 100. Поскольку минимальным является 100, то вычитаем его.
x14 = min(120,100) = 100.
| 8 | x | 10 | 9 | 0 | 120 - 100 = 20 |
| x | 8 | 8 | x | x | 0 |
| x | x | 9 | x | 0 | 130 |
| x | x | 8 | x | x | 0 |
| 0 | 0 | 50 | 100 - 100 = 0 | 100 | 0 |
Для этого элемента запасы равны 130, потребности 50. Поскольку минимальным является 50, то вычитаем его.
x33 = min(130,50) = 50.
| 8 | x | x | 9 | 0 | 20 |
| x | 8 | 8 | x | x | 0 |
| x | x | 9 | x | 0 | 130 - 50 = 80 |
| x | x | 8 | x | x | 0 |
| 0 | 0 | 50 - 50 = 0 | 0 | 100 | 0 |
Для этого элемента запасы равны 20, потребности 100. Поскольку минимальным является 20, то вычитаем его.
x15 = min(20,100) = 20.
| 8 | x | x | 9 | 0 | 20 - 20 = 0 |
| x | 8 | 8 | x | x | 0 |
| x | x | 9 | x | 0 | 80 |
| x | x | 8 | x | x | 0 |
| 0 | 0 | 0 | 0 | 100 - 20 = 80 | 0 |
Для этого элемента запасы равны 80, потребности 80. Поскольку минимальным является 80, то вычитаем его.
x35 = min(80,80) = 80.
| 8 | x | x | 9 | 0 | 0 |
| x | 8 | 8 | x | x | 0 |
| x | x | 9 | x | 0 | 80 - 80 = 0 |
| x | x | 8 | x | x | 0 |
| 0 | 0 | 0 | 0 | 80 - 80 = 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | Запасы | |
| 1 | 8[60] | 9 | 10 | 9[100] | 0[20] | 180 |
| 2 | 10 | 8[80] | 8[120] | 9 | 0 | 200 |
| 3 | 11 | 10 | 9[50] | 10 | 0[80] | 130 |
| 4 | 9 | 9 | 8[50] | 10 | 0 | 50 |
| Потребности | 60 | 80 | 220 | 100 | 100 |
2. Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 8. Следовательно, опорный план является невырожденным.
Значение целевой функции для этого опорного плана равно:
F(x) = 8*60 + 9*100 + 0*20 + 8*80 + 8*120 + 9*50 + 0*80 + 8*50 = 3830
Этап II. Улучшение опорного плана.
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
u1 + v1 = 8; 0 + v1 = 8; v1 = 8
u1 + v4 = 9; 0 + v4 = 9; v4 = 9
u1 + v5 = 0; 0 + v5 = 0; v5 = 0
u3 + v5 = 0; 0 + u3 = 0; u3 = 0
u3 + v3 = 9; 0 + v3 = 9; v3 = 9
u2 + v3 = 8; 9 + u2 = 8; u2 = -1
u2 + v2 = 8; -1 + v2 = 8; v2 = 9
u4 + v3 = 8; 9 + u4 = 8; u4 = -1
| v1=8 | v2=9 | v3=9 | v4=9 | v5=0 | |
| u1=0 | 8[60] | 9 | 10 | 9[100] | 0[20] |
| u2=-1 | 10 | 8[80] | 8[120] | 9 | 0 |
| u3=0 | 11 | 10 | 9[50] | 10 | 0[80] |
| u4=-1 | 9 | 9 | 8[50] | 10 | 0 |
Минимальные затраты составят:
F(x) = 8*60 + 9*100 + 0*20 + 8*80 + 8*120 + 9*50 + 0*80 + 8*50 = 3830
Проверим оптимальность найденного плана по первой теореме двойственности (в оптимальном решении значения целевых функций прямой и двойственных задач совпадают: F = G).
G = 0•180 -1•200 + 0•130 -1•50 + 8•60 + 9•80 + 9•220 + 9•100 + 0•100 = 3830
Пример. Необходимо найти решение транспортной задачи по критерию стоимости методом потенциалов.
В силу специфических особенностей структуры математической модели транспортной ЗЛП разработаны для ее решения менее трудоемкие методы, чем симплекс-метод. Наибольшее применение нашел метод потенциалов, базирующийся на утверждениях теорем двойственности. Опорное решение ТЗЛП можно находить любым из предлагаемых методов. Для решения воспользуемся сервисом Транспортная задача онлайн
.
| 26 | 30 | 17 | 10 | 16 | 4 |
| 30 | 37 | 26 | 9 | 23 | 6 |
| 13 | 4 | 32 | 3 | 1 | 10 |
| 3 | 1 | 5 | 14 | 24 | 10 |
| 7 | 7 | 7 | 7 | 2 |
Решение:
Проверим необходимое и достаточное условие разрешимости задачи.
∑ a = 4 + 6 + 10 + 10 = 30
∑ b = 7 + 7 + 7 + 7 + 2 = 30
Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
Занесем исходные данные в распределительную таблицу.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17 |
10 | 16 |
4 |
2 | 30 | 37 | 26 | 9 | 23 | 6 |
|
3 | 13 |
4 | 32 |
3 | 1 |
10 |
4 | 3 | 1 | 5 | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
Искомый элемент равен 1.
Для этого элемента запасы равны 10, потребности 2. Поскольку минимальным является 2, то вычитаем его.
26 | 30 | 17 | 10 | x | 4 |
30 |
37 | 26 |
9 | x |
6 |
13 | 4 | 32 | 3 | 1 | 8 |
3 |
1 | 5 |
14 | x |
10 |
7 | 7 | 7 | 7 | 0 | 0 |
Искомый элемент равен 1.
Для этого элемента запасы равны 10, потребности 7. Поскольку минимальным является 7, то вычитаем его.
26 | x | 17 | 10 | x | 4 |
30 |
x | 26 |
9 | x |
6 |
13 | x | 32 | 3 | 1 | 8 |
3 |
1 | 5 |
14 | x |
3 |
7 | 0 | 7 | 7 | 0 | 0 |
Искомый элемент равен 3.
Для этого элемента запасы равны 8, потребности 7. Поскольку минимальным является 7, то вычитаем его.
26 | x | 17 | x | x | 4 |
30 |
x | 26 |
x | x |
6 |
13 | x | 32 | 3 | 1 | 1 |
3 |
1 | 5 |
x | x |
3 |
7 | 0 | 7 | 0 | 0 | 0 |
Искомый элемент равен 3.
Для этого элемента запасы равны 3, потребности 7. Поскольку минимальным является 3, то вычитаем его.
26 | x | 17 | x | x | 4 |
30 |
x | 26 |
x | x |
6 |
13 | x | 32 | 3 | 1 | 1 |
3 |
1 | x |
x | x |
0 |
4 | 0 | 7 | 0 | 0 | 0 |
Искомый элемент равен 13.
Для этого элемента запасы равны 1, потребности 4. Поскольку минимальным является 1, то вычитаем его.
26 | x | 17 | x | x | 4 |
30 |
x | 26 |
x | x |
6 |
13 | x | x | 3 | 1 | 0 |
3 |
1 | x |
x | x |
0 |
3 | 0 | 7 | 0 | 0 | 0 |
Искомый элемент равен 17.
Для этого элемента запасы равны 4, потребности 7. Поскольку минимальным является 4, то вычитаем его.
x | x | 17 | x | x | 0 |
30 |
x | 26 |
x | x |
6 |
13 | x | x | 3 | 1 | 0 |
3 |
1 | x |
x | x |
0 |
3 | 0 | 3 | 0 | 0 | 0 |
Искомый элемент равен 26.
Для этого элемента запасы равны 6, потребности 3. Поскольку минимальным является 3, то вычитаем его.
x | x | 17 | x | x | 0 |
30 |
x | 26 |
x | x |
3 |
13 | x | x | 3 | 1 | 0 |
3 |
1 | x |
x | x |
0 |
3 | 0 | 0 | 0 | 0 | 0 |
Искомый элемент равен 30.
Для этого элемента запасы равны 3, потребности 3. Поскольку минимальным является 3, то вычитаем его.
x | x | 17 | x | x | 0 |
30 |
x | 26 |
x | x |
0 |
13 | x | x | 3 | 1 | 0 |
3 |
1 | x |
x | x |
0 |
0 | 0 | 0 | 0 | 0 | 0 |
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30[3] | 37 | 26[3] | 9 | 23 | 6 |
|
3 | 13[1] |
4 | 32 |
3[7] | 1[2] |
10 |
4 | 3[3] | 1[7] | 5 | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.
2. Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 8. Следовательно, опорный план является невырожденным.
4. Проверим оптимальность опорного плана. Найдем потенциалы uiи vjпо занятым клеткам таблицы, в которых ui+ vj= cij, полагая, что u1= 0.
u1 + v3 = 17; 0 + v3 = 17; v3 = 17
u2 + v3 = 26; 17 + u2 = 26; u2 = 9
u2 + v1 = 30; 9 + v1 = 30; v1 = 21
u3 + v1 = 13; 21 + u3 = 13; u3 = -8
u3 + v4 = 3; -8 + v4 = 3; v4 = 11
u3 + v5 = 1; -8 + v5 = 1; v5 = 9
u4 + v1 = 3; 21 + u4 = 3; u4 = -18
u4 + v2 = 1; -18 + v2 = 1; v2 = 19
v1=21 | v2=19 | v3=17 | v4=11 | v5=9 | |
u1=0 |
26 | 30 |
17[4] | 10 |
16 |
u2=9 | 30[3] | 37 | 26[3] | 9 | 23 |
u3=-8 |
13[1] | 4 |
32 | 3[7] |
1[2] |
u4=-18 | 3[3] | 1[7] | 5 | 14 | 24 |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui+vj> cij
(1;4): 0 + 11 > 10; ∆14= 0 + 11 - 10 = 1
(2;4): 9 + 11 > 9; ∆24= 9 + 11 - 9 = 11
(3;2): -8 + 19 > 4; ∆32= -8 + 19 - 4 = 7
max(1,11,7) = 11 Выбираем максимальную оценку свободной клетки (2;4): 9.
Для этого в перспективную клетку (2;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-». Цикл приведен в таблице.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30[3][-] | 37 | 26[3] | 9[+] | 23 | 6 |
|
3 | 13[1][+] |
4 | 32 |
3[7][-] | 1[2] |
10 |
4 | 3[3] | 1[7] | 5 | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 1) = 3. Прибавляем 3 к объемам грузов, стоящих в плюсовых клетках и вычитаем 3 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30 | 37 | 26[3] | 9[3] | 23 | 6 |
|
3 | 13[4] |
4 | 32 |
3[4] | 1[2] |
10 |
4 | 3[3] | 1[7] | 5 | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
u1 + v3 = 17; 0 + v3 = 17; v3 = 17
u2 + v3 = 26; 17 + u2 = 26; u2 = 9
u2 + v4 = 9; 9 + v4 = 9; v4 = 0
u3 + v4 = 3; 0 + u3 = 3; u3 = 3
u3 + v1 = 13; 3 + v1 = 13; v1 = 10
u4 + v1 = 3; 10 + u4 = 3; u4 = -7
u4 + v2 = 1; -7 + v2 = 1; v2 = 8
u3 + v5 = 1; 3 + v5 = 1; v5 = -2
v1=10 | v2=8 | v3=17 | v4=0 | v5=-2 | |
u1=0 |
26 | 30 |
17[4] | 10 |
16 |
u2=9 | 30 | 37 | 26[3] | 9[3] | 23 |
u3=3 |
13[4] | 4 |
32 | 3[4] |
1[2] |
u4=-7 | 3[3] | 1[7] | 5 | 14 | 24 |
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui+vj> cij
(3;2): 3 + 8 > 4; ∆32= 3 + 8 - 4 = 7
(4;3): -7 + 17 > 5; ∆43= -7 + 17 - 5 = 5
max(7,5) = 7
Выбираем максимальную оценку свободной клетки (3;2): 4.
Для этого в перспективную клетку (3;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-». Цикл приведен в таблице.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30 | 37 | 26[3] | 9[3] | 23 | 6 |
|
3 | 13[4][-] |
4[+] | 32 |
3[4] | 1[2] |
10 |
4 | 3[3][+] | 1[7][-] | 5 | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 1) = 4. Прибавляем 4 к объемам грузов, стоящих в плюсовых клетках и вычитаем 4 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30 | 37 | 26[3] | 9[3] | 23 | 6 |
|
3 | 13 |
4[4] | 32 |
3[4] | 1[2] |
10 |
4 | 3[7] | 1[3] | 5 | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
u1 + v3 = 17; 0 + v3 = 17; v3 = 17
u2 + v3 = 26; 17 + u2 = 26; u2 = 9
u2 + v4 = 9; 9 + v4 = 9; v4 = 0
u3 + v4 = 3; 0 + u3 = 3; u3 = 3
u3 + v2 = 4; 3 + v2 = 4; v2 = 1
u4 + v2 = 1; 1 + u4 = 1; u4 = 0
u4 + v1 = 3; 0 + v1 = 3; v1 = 3
u3 + v5 = 1; 3 + v5 = 1; v5 = -2
v1=3 | v2=1 | v3=17 | v4=0 | v5=-2 | |
u1=0 |
26 | 30 |
17[4] | 10 |
16 |
u2=9 | 30 | 37 | 26[3] | 9[3] | 23 |
u3=3 |
13 | 4[4] |
32 | 3[4] |
1[2] |
u4=0 | 3[7] | 1[3] | 5 | 14 | 24 |
Опорный план не является оптимальным, так как существуют оценки свободных клеток.
(4;3): 0 + 17 > 5; ∆43= 0 + 17 - 5 = 12
Выбираем максимальную оценку свободной клетки (4;3): 5
Для этого в перспективную клетку (4;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-». Цикл приведен в таблице.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30 | 37 | 26[3][-] | 9[3][+] | 23 | 6 |
|
3 | 13 |
4[4][+] | 32 |
3[4][-] | 1[2] |
10 |
4 | 3[7] | 1[3][-] | 5[+] | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (4, 2) = 3. Прибавляем 3 к объемам грузов, стоящих в плюсовых клетках и вычитаем 3 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30 | 37 | 26[0] | 9[6] | 23 | 6 |
|
3 | 13 |
4[7] | 32 |
3[1] | 1[2] |
10 |
4 | 3[7] | 1 | 5[3] | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
u1 + v3 = 17; 0 + v3 = 17; v3 = 17
u2 + v3 = 26; 17 + u2 = 26; u2 = 9
u2 + v4 = 9; 9 + v4 = 9; v4 = 0
u3 + v4 = 3; 0 + u3 = 3; u3 = 3
u3 + v2 = 4; 3 + v2 = 4; v2 = 1
u3 + v5 = 1; 3 + v5 = 1; v5 = -2
u4 + v3 = 5; 17 + u4 = 5; u4 = -12
u4 + v1 = 3; -12 + v1 = 3; v1 = 15
v1=15 | v2=1 | v3=17 | v4=0 | v5=-2 | |
u1=0 |
26 | 30 |
17[4] | 10 |
16 |
u2=9 | 30 | 37 | 26[0] | 9[6] | 23 |
u3=3 |
13 | 4[7] |
32 | 3[1] |
1[2] |
u4=-12 | 3[7] | 1 | 5[3] | 14 | 24 |
Опорный план не является оптимальным, так как существуют оценки свободных клеток.
(3;1): 3 + 15 > 13; ∆31= 3 + 15 - 13 = 5.
Выбираем максимальную оценку свободной клетки (3;1): 13
Для этого в перспективную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-». Цикл приведен в таблице.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30 | 37 | 26[0][-] | 9[6][+] | 23 | 6 |
|
3 | 13[+] |
4[7] | 32 |
3[1][-] | 1[2] |
10 |
4 | 3[7][-] | 1 | 5[3][+] | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 0. Прибавляем 0 к объемам грузов, стоящих в плюсовых клетках и вычитаем 0 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
1 | 2 | 3 | 4 | 5 | Запасы | |
|
1 | 26 |
30 | 17[4] |
10 | 16 |
4 |
2 | 30 | 37 | 26 | 9[6] | 23 | 6 |
|
3 | 13[0] |
4[7] | 32 |
3[1] | 1[2] |
10 |
4 | 3[7] | 1 | 5[3] | 14 | 24 | 10 |
|
Потребности | 7 |
7 | 7 |
7 | 2 |
|
u1 + v3 = 17; 0 + v3 = 17; v3 = 17
u4 + v3 = 5; 17 + u4 = 5; u4 = -12
u4 + v1 = 3; -12 + v1 = 3; v1 = 15
u3 + v1 = 13; 15 + u3 = 13; u3 = -2
u3 + v2 = 4; -2 + v2 = 4; v2 = 6
u3 + v4 = 3; -2 + v4 = 3; v4 = 5
u2 + v4 = 9; 5 + u2 = 9; u2 = 4
u3 + v5 = 1; -2 + v5 = 1; v5 = 3
v1=15 | v2=6 | v3=17 | v4=5 | v5=3 | |
u1=0 |
26 | 30 |
17[4] | 10 |
16 |
u2=4 | 30 | 37 | 26 | 9[6] | 23 |
u3=-2 |
13[0] | 4[7] |
32 | 3[1] |
1[2] |
u4=-12 | 3[7] | 1 | 5[3] | 14 | 24 |
Опорный план является оптимальным. Минимальные затраты составят:
F(x) = 17*4 + 9*6 + 4*7 + 3*1 + 1*2 + 3*7 + 5*3 = 191
Пример №4.
Ниже приведены числовые данные транспортных задач. Стоимость перевозки единицы продукции записаны в клетках таблицы. Запасы указаны справа от таблиц, а потребности – снизу. Требуется построить начальный план методами: «северо-западного угла», «минимального элемента», «двойного предпочтения», методом Фогеля. Из каждого плана найти оптимальный план методом потенциалов.
Решение:
а) Методом потенциалов. Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3 | 7 | 1 | 10 |
| 2 | 5 | 12 | 10 | 4 | 29 |
| 3 | 16 | 8 | 2 | 9 | 39 |
| 4 | 5 | 11 | 10 | 3 | 49 |
| 5 | 0 | 0 | 0 | 0 | 34 |
| Потребности | 19 | 35 | 42 | 65 |
∑a = 10 + 29 + 39 + 49 + 34 = 161
∑b = 19 + 35 + 42 + 65 = 161
Условие баланса соблюдается.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3 | 7 | 1 | 10 |
| 2 | 5 | 12 | 10 | 4 | 29 |
| 3 | 16 | 8 | 2 | 9 | 39 |
| 4 | 5 | 11 | 10 | 3 | 49 |
| 5 | 0 | 0 | 0 | 0 | 34 |
| Потребности | 19 | 35 | 42 | 65 |
1. Используя метод северо-западного угла, построим первый опорный план транспортной задачи. План начинается заполняться с верхнего левого угла. Искомый элемент равен 6. Для этого элемента запасы равны 10, потребности 19. Поскольку минимальным является 10, то вычитаем его.
x11= min(10,19) = 10.
| 6 | x | x | x | 10 - 10 = 0 |
| 5 | 12 | 10 | 4 | 29 |
| 16 | 8 | 2 | 9 | 39 |
| 5 | 11 | 10 | 3 | 49 |
| 0 | 0 | 0 | 0 | 34 |
| 19 - 10 = 9 | 35 | 42 | 65 | 0 |
x21= min(29,9) = 9.
| 6 | x | x | x | 0 |
| 5 | 12 | 10 | 4 | 29 - 9 = 20 |
| x | 8 | 2 | 9 | 39 |
| x | 11 | 10 | 3 | 49 |
| 0 | 0 | 0 | 0 | 34 |
| 9 - 9 = 0 | 35 | 42 | 65 | 0 |
x22= min(20,35) = 20.
| 6 | x | x | x | 0 |
| 5 | 12 | x | x | 20 - 20 = 0 |
| x | 8 | 2 | 9 | 39 |
| x | 11 | 10 | 3 | 49 |
| 0 | 0 | 0 | 0 | 34 |
| 0 | 35 - 20 = 15 | 42 | 65 | 0 |
x32= min(39,15) = 15.
| 6 | x | x | x | 0 |
| 5 | 12 | x | x | 0 |
| x | 8 | 2 | 9 | 39 - 15 = 24 |
| x | x | 10 | 3 | 49 |
| 0 | 0 | 0 | 0 | 34 |
| 0 | 15 - 15 = 0 | 42 | 65 | 0 |
x33= min(24,42) = 24.
| 6 | x | x | x | 0 |
| 5 | 12 | x | x | 0 |
| x | 8 | 2 | x | 24 - 24 = 0 |
| x | x | 10 | 3 | 49 |
| 0 | 0 | 0 | 0 | 34 |
| 0 | 0 | 42 - 24 = 18 | 65 | 0 |
x43= min(49,18) = 18.
| 6 | x | x | x | 0 |
| 5 | 12 | x | x | 0 |
| x | 8 | 2 | x | 0 |
| x | x | 10 | 3 | 49 - 18 = 31 |
| 0 | 0 | 0 | 0 | 34 |
| 0 | 0 | 18 - 18 = 0 | 65 | 0 |
x44= min(31,65) = 31.
| 6 | x | x | x | 0 |
| 5 | 12 | x | x | 0 |
| x | 8 | 2 | x | 0 |
| x | x | 10 | 3 | 31 - 31 = 0 |
| 0 | 0 | 0 | 0 | 34 |
| 0 | 0 | 0 | 65 - 31 = 34 | 0 |
x54= min(34,34) = 34.
| 6 | x | x | x | 0 |
| 5 | 12 | x | x | 0 |
| x | 8 | 2 | x | 0 |
| x | x | 10 | 3 | 0 |
| 0 | 0 | 0 | 0 | 34 - 34 = 0 |
| 0 | 0 | 0 | 34 - 34 = 0 | 0 |
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10] | 3 | 7 | 1 | 10 |
| 2 | 5[9] | 12[20] | 10 | 4 | 29 |
| 3 | 16 | 8[15] | 2[24] | 9 | 39 |
| 4 | 5 | 11 | 10[18] | 3[31] | 49 |
| 5 | 0 | 0 | 0 | 0[34] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
2. Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 8. Следовательно, опорный план является невырожденным.
Значение целевой функции для этого опорного плана равно: F(x) = 6*10 + 5*9 + 12*20 + 8*15 + 2*24 + 10*18 + 3*31 +0*34 = 786
4. Проверим оптимальность опорного плана. Найдем предварительные потенциалыui, vj. по занятым клеткам таблицы, в которых ui+ vj= cij, полагая, что u1= 0.
u1+ v1= 6; 0 + v1= 6; v1= 6
u2+ v2= 12; -1 + v2= 12; v2= 13
u3+ v3= 2; -5 + v3= 2; v3= 7
u4+ v4= 3;3 + v4= 3; v4= 0
| v1=6 | v2=13 | v3=7 | v4=0 | |
| u1=0 | 6[10] | 3 | 7 | 1 |
| u2=-1 | 5[9] | 12[20] | 10 | 4 |
| u3=-5 | 16 | 8[15] | 2[24] | 9 |
| u4=3 | 5 | 11 | 10[18] | 3[31] |
| u5=0 | 0 | 0 | 0 | 0[34] |
(1;2): 0 + 13 > 3; ∆12= 0 + 13 - 3 =10
(4;1): 3 + 6 > 5; ∆41= 3 + 6 - 5 = 4
(4;2): 3 + 13 > 11; ∆42= 3 + 13 - 11 =5
(5;1): 0 + 6 > 0; ∆51= 0 + 6 - 0 = 6
(5;2): 0 + 13 > 0; ∆52= 0 + 13 - 0 =13
(5;3): 0 + 7 > 0; ∆53= 0 + 7 - 0 = 7
max(10,4,5,6,13,7) = 13
Выбираем максимальную оценку свободной клетки (5;2): 0
Для этого в перспективную клетку (5;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10] | 3 | 7 | 1 | 10 |
| 2 | 5[9] | 12[20] | 10 | 4 | 29 |
| 3 | 16 | 8[15][-] | 2[24][+] | 9 | 39 |
| 4 | 5 | 11 | 10[18][-] | 3[31][+] | 49 |
| 5 | 0 | 0[+] | 0 | 0[34][-] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 2) = 15. Прибавляем 15 к объемам грузов, стоящих в плюсовых клетках и вычитаем 15 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10] | 3 | 7 | 1 | 10 |
| 2 | 5[9] | 12[20] | 10 | 4 | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10[3] | 3[46] | 49 |
| 5 | 0 | 0[15] | 0 | 0[19] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
u1+ v1= 6; 0 + v1= 6; v1= 6
u2+ v2= 12; -1 + v2= 12; v2= 13
u5+ v4= 0; -13 + v4= 0; v4= 13
u4+ v3= 10;-10 + v3= 10; v3= 20
| v1=6 | v2=13 | v3=20 | v4=13 | |
| u1=0 | 6[10] | 3 | 7 | 1 |
| u2=-1 | 5[9] | 12[20] | 10 | 4 |
| u3=-18 | 16 | 8 | 2[39] | 9 |
| u4=-10 | 5 | 11 | 10[3] | 3[46] |
| u5=-13 | 0 | 0[15] | 0 | 0[19] |
(1;2): 0 + 13 > 3; ∆12= 0 + 13 - 3 =10
(1;3): 0 + 20 > 7; ∆13= 0 + 20 - 7 =13
(1;4): 0 + 13 > 1; ∆14= 0 + 13 - 1 =12
(2;3): -1 + 20 > 10; ∆23= -1 + 20 - 10= 9
(2;4): -1 + 13 > 4; ∆24= -1 + 13 - 4 =8
(5;3): -13 + 20 > 0; ∆53= -13 + 20 - 0= 7
max(10,13,12,9,8,7) = 13
Выбираем максимальную оценку свободной клетки (1;3): 7
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[10][-] | 3 | 7[+] | 1 | 10 |
| 2 | 5[9][+] | 12[20][-] | 10 | 4 | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10[3][-] | 3[46][+] | 49 |
| 5 | 0 | 0[15][+] | 0 | 0[19][-] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (4, 3) = 3. Прибавляем 3 к объемам грузов, стоящих в плюсовых клетках и вычитаем 3 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[7] | 3 | 7[3] | 1 | 10 |
| 2 | 5[12] | 12[17] | 10 | 4 | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[18] | 0 | 0[16] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
u1+ v1= 6; 0 + v1= 6; v1= 6
u2+ v2= 12; -1 + v2= 12; v2= 13
u5+ v4= 0; -13 + v4= 0; v4= 13
u1+ v3= 7;0 + v3= 7; v3= 7
| v1=6 | v2=13 | v3=7 | v4=13 | |
| u1=0 | 6[7] | 3 | 7[3] | 1 |
| u2=-1 | 5[12] | 12[17] | 10 | 4 |
| u3=-5 | 16 | 8 | 2[39] | 9 |
| u4=-10 | 5 | 11 | 10 | 3[49] |
| u5=-13 | 0 | 0[18] | 0 | 0[16] |
(1;2): 0 + 13 > 3; ∆12= 0 + 13 - 3 =10
(1;4): 0 + 13 > 1; ∆14= 0 + 13 - 1 =12
(2;4): -1 + 13 > 4; ∆24= -1 + 13 - 4 =8
max(10,12,8) = 12
Выбираем максимальную оценку свободной клетки (1;4): 1
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6[7][-] | 3 | 7[3] | 1[+] | 10 |
| 2 | 5[12][+] | 12[17][-] | 10 | 4 | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[18][+] | 0 | 0[16][-] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 1) = 7. Прибавляем 7 к объемам грузов, стоящих в плюсовых клетках и вычитаем 7 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3 | 7[3] | 1[7] | 10 |
| 2 | 5[19] | 12[10] | 10 | 4 | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[25] | 0 | 0[9] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
u1+ v3= 7; 0 + v3= 7; v3= 7
u1+ v4= 1; 0 + v4= 1; v4= 1
u5+ v2= 0; -1 + v2= 0; v2= 1
u2+ v1= 5;11 + v1= 5; v1= -6
| v1=-6 | v2=1 | v3=7 | v4=1 | |
| u1=0 | 6 | 3 | 7[3] | 1[7] |
| u2=11 | 5[19] | 12[10] | 10 | 4 |
| u3=-5 | 16 | 8 | 2[39] | 9 |
| u4=2 | 5 | 11 | 10 | 3[49] |
| u5=-1 | 0 | 0[25] | 0 | 0[9] |
(2;3): 11 + 7 > 10; ∆23= 11 + 7 - 10 =8
(2;4): 11 + 1 > 4; ∆24= 11 + 1 - 4 = 8
(5;3): -1 + 7 > 0; ∆53= -1 + 7 - 0 = 6
max(8,8,6) = 8
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3 | 7[3][-] | 1[7][+] | 10 |
| 2 | 5[19] | 12[10][-] | 10[+] | 4 | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[25][+] | 0 | 0[9][-] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 3) = 3. Прибавляем 3 к объемам грузов, стоящих в плюсовых клетках и вычитаем 3 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3 | 7 | 1[10] | 10 |
| 2 | 5[19] | 12[7] | 10[3] | 4 | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[28] | 0 | 0[6] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
u1+ v4= 1; 0 + v4= 1; v4= 1
u5+ v2= 0; -1 + v2= 0; v2= 1
u2+ v1= 5; 11 + v1= 5; v1= -6
u2+ v3= 10;11 + v3= 10; v3= -1
| v1=-6 | v2=1 | v3=-1 | v4=1 | |
| u1=0 | 6 | 3 | 7 | 1[10] |
| u2=11 | 5[19] | 12[7] | 10[3] | 4 |
| u3=3 | 16 | 8 | 2[39] | 9 |
| u4=2 | 5 | 11 | 10 | 3[49] |
| u5=-1 | 0 | 0[28] | 0 | 0[6] |
(2;4): 11 + 1 > 4; ∆24= 11 + 1 - 4 = 8
Выбираем максимальную оценку свободной клетки (2;4): 4
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3 | 7 | 1[10] | 10 |
| 2 | 5[19] | 12[7][-] | 10[3] | 4[+] | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[28][+] | 0 | 0[6][-] | 34 |
| Потребности | 19 | 35 | 42 | 65 |
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (5, 4) = 6.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3 | 7 | 1[10] | 10 |
| 2 | 5[19] | 12[1] | 10[3] | 4[6] | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[34] | 0 | 0 | 34 |
| Потребности | 19 | 35 | 42 | 65 |
u1+ v4= 1; 0 + v4= 1; v4= 1
u2+ v1= 5; 3 + v1= 5; v1= 2
u2+ v2= 12; 3 + v2= 12; v2= 9
u2+ v3= 10;3 + v3= 10; v3= 7
| v1=2 | v2=9 | v3=7 | v4=1 | |
| u1=0 | 6 | 3 | 7 | 1[10] |
| u2=3 | 5[19] | 12[1] | 10[3] | 4[6] |
| u3=-5 | 16 | 8 | 2[39] | 9 |
| u4=2 | 5 | 11 | 10 | 3[49] |
| u5=-9 | 0 | 0[34] | 0 | 0 |
(1;2): 0 + 9 > 3; ∆12= 0 + 9 - 3 = 6
Выбираем максимальную оценку свободной клетки (1;2): 3
Для этого в перспективную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3[+] | 7 | 1[10][-] | 10 |
| 2 | 5[19] | 12[1][-] | 10[3] | 4[6][+] | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[34] | 0 | 0 | 34 |
| Потребности | 19 | 35 | 42 | 65 |
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 2) = 1.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3[1] | 7 | 1[9] | 10 |
| 2 | 5[19] | 12 | 10[3] | 4[7] | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[34] | 0 | 0 | 34 |
| Потребности | 19 | 35 | 42 | 65 |
u1+ v2= 3; 0 + v2= 3; v2= 3
u1+ v4= 1; 0 + v4= 1; v4= 1
u2+ v1= 5; 3 + v1= 5; v1= 2
u2+ v3= 10;3 + v3= 10; v3= 7
| v1=2 | v2=3 | v3=7 | v4=1 | |
| u1=0 | 6 | 3[1] | 7 | 1[9] |
| u2=3 | 5[19] | 12 | 10[3] | 4[7] |
| u3=-5 | 16 | 8 | 2[39] | 9 |
| u4=2 | 5 | 11 | 10 | 3[49] |
| u5=-3 | 0 | 0[34] | 0 | 0 |
(5;3): -3 + 7 > 0; ∆53= -3 + 7 - 0 = 4
Выбираем максимальную оценку свободной клетки (5;3): 0
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3[1][+] | 7 | 1[9][-] | 10 |
| 2 | 5[19] | 12 | 10[3][-] | 4[7][+] | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[34][-] | 0[+] | 0 | 34 |
| Потребности | 19 | 35 | 42 | 65 |
Из грузов хijстоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 3.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 6 | 3[4] | 7 | 1[6] | 10 |
| 2 | 5[19] | 12 | 10 | 4[10] | 29 |
| 3 | 16 | 8 | 2[39] | 9 | 39 |
| 4 | 5 | 11 | 10 | 3[49] | 49 |
| 5 | 0 | 0[31] | 0[3] | 0 | 34 |
| Потребности | 19 | 35 | 42 | 65 |
u1+ v2= 3; 0 + v2= 3; v2= 3
u5+ v3= 0; -3 + v3= 0; v3= 3
u1+ v4= 1; 0 + v4= 1; v4= 1
u2+ v1= 5;3 + v1= 5; v1= 2
| v1=2 | v2=3 | v3=3 | v4=1 | |
| u1=0 | 6 | 3[4] | 7 | 1[6] |
| u2=3 | 5[19] | 12 | 10 | 4[10] |
| u3=-1 | 16 | 8 | 2[39] | 9 |
| u4=2 | 5 | 11 | 10 | 3[49] |
| u5=-3 | 0 | 0[31] | 0[3] | 0 |
Минимальные затраты составят: F(x) = 3*4 + 1*6 + 5*19 + 4*10 + 2*39 + 3*49 + 0*31 + 0*3 = 378