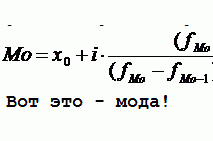Абсолютная ошибка аппроксимации

Расчет абсолютных и/или относительных ошибок. Часто рассчитывают: среднюю абсолютную процентную ошибку (Mean Absolute Percentage Error):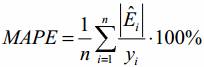

Если модель подогнана с высокой точностью MAPE<10%, хорошей - 10% < MAPE < 20%, удовлетворительной - 20% < MAPE < 50%, неудовлетворительной - MAPE > 50%.
Целесообразно пропускать значения ряда, для которых y_i=0.
Средняя процентная ошибка (Mean Percentage Error) и средняя ошибка (Mean Error). Средняя процентная ошибка не определена при нулевых данных и не должна превышать 5% для хорошо подогнанной модели:

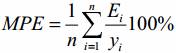
Средняя ошибка:

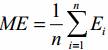
случайная компонента получается как разность E=y-y(x)

Пример. 1. Находим параметры уравнения методом наименьших квадратов .
Линейное уравнение тренда имеет вид y=at+b (Тренд — систематическая составляющая временного ряда).
Система уравнений

Для наших данных система уравнений имеет вид

Из первого уравнения выражаем а₀ и подставим во второе уравнение
Получаем a₀ = -4.13, a₁ = 78.57
Уравнение тренда: y = -4.13 t + 78.57
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда.
Средние значения:

Дисперсия

Среднеквадратическое отклонение

Коэффициент детерминации

т.е. в 78.66 % случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда - высокая

t	y	t²	y²	t•y	y(t)	(y-y _cp)²	(y-y(t))²	(t-t _p)²	(y-y(t)) : y
1	80	1	6400	80	74.44	1653.78	30.93	72.25	444.91
2	79	4	6241	158	70.31	1573.44	75.54	56.25	686.62
3	75	9	5625	225	66.18	1272.11	77.82	42.25	661.61
4	70	16	4900	280	62.05	940.44	63.23	30.25	556.6
5	65	25	4225	325	57.92	658.78	50.15	20.25	460.3
6	60	36	3600	360	53.79	427.11	38.58	12.25	372.69
7	39	49	1521	273	49.66	0.11	113.6	6.25	415.68
8	35	64	1225	280	45.53	18.78	110.85	2.25	368.49
9	30	81	900	270	41.4	87.11	129.92	0.25	341.95
10	25	100	625	250	37.27	205.44	150.51	0.25	306.71
11	20	121	400	220	33.14	373.78	172.61	2.25	262.77
12	10	144	100	120	29.01	860.44	361.31	6.25	190.08
13	13	169	169	169	24.88	693.44	141.09	12.25	154.42
14	19	196	361	266	20.75	413.44	3.06	20.25	33.22
15	29	225	841	435	16.62	106.78	153.31	30.25	359.07
16	14	256	196	224	12.49	641.78	2.29	42.25	21.17
17	20	289	400	340	8.36	373.78	135.53	56.25	232.84
18	25	324	625	450	4.23	205.44	431.47	72.25	519.3
171	708	2109	38354	4725	708	10506	2241.81	484.5	6388.43

2) F-статистика. Критерий Фишера.

Fkp = 4.45
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.

y	y(x)	e_i = y-y(x)	e²	(e_i - e_i-1)²
80	74.44	5.56	30.93	0
79	70.31	8.69	75.54	9.8
75	66.18	8.82	77.82	0.02
70	62.05	7.95	63.23	0.76
65	57.92	7.08	50.15	0.76
60	53.79	6.21	38.58	0.76
39	49.66	-10.66	113.6	284.6
35	45.53	-10.53	110.85	0.02
30	41.4	-11.4	129.92	0.76
25	37.27	-12.27	150.51	0.76
20	33.14	-13.14	172.61	0.76
10	29.01	-19.01	361.31	34.46
13	24.88	-11.88	141.09	50.84
19	20.75	-1.75	3.06	102.62
29	16.62	12.38	153.31	199.66
14	12.49	1.51	2.29	118.16
20	8.36	11.64	135.53	102.62
25	4.23	20.77	431.47	83.36
			2241.81	990.67

Критические значения d₁ и d₂ определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 < DW < 2.5. Для более надежного вывода целесообразно обращаться к табличным значениям.
d₁ < DW и d₂ < DW < 4 - d₂.

Пример №2. Исследовать динамику экономического показателя на основе анализа одномерного временного ряда.
В течение девяти последовательных недель фиксировался спрос Y(t) (млн руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя (повариантно) приведен ниже в таблице.

Решение проводим при помощь онлайн калькулятора Линейное уравнение тренда.
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a₀n + a₁∑t = ∑y
a₀∑t + a₁∑t² = ∑y•t
Для наших данных система уравнений имеет вид:
9a₀ + 45a₁ = 390
45a₀ + 285a₁ = 2094
Из первого уравнения выражаем а₀ и подставим во второе уравнение
Получаем a₀ = 2.4, a₁ = 31.33
Уравнение тренда:
y = 2.4 t + 31.33
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов β_i, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = 2.4 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на 2.4.
Ошибка аппроксимации.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.

Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.

Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.

t	y	t²	y²	t•y	y(t)	(y-y(t)) : y
1	33	1	1089	33	33.73	0.0222
2	35	4	1225	70	36.13	0.0324
3	40	9	1600	120	38.53	0.0367
4	41	16	1681	164	40.93	0.00163
5	45	25	2025	225	43.33	0.037
6	47	36	2209	282	45.73	0.027
7	45	49	2025	315	48.13	0.0696
8	51	64	2601	408	50.53	0.00915
9	53	81	2809	477	52.93	0.00126
45	390	285	17264	2094	390	0.24

Перейти к онлайн решению своей задачи

Абсолютная ошибка аппроксимации

Правила ввода данных

Поиск

Процесс

Сообщение