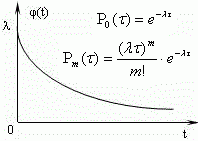СМО с ожиданием (очередью)
Системы с ожиданием при неограниченном входящем потоке
На n одинаковых каналов поступает простейший поток заявок интенсивностью λ. Если в момент поступления заявки все каналы заняты, то эта заявка становится в очередь и ждет начала облуживания. Время обслуживания каждой заявки является случайной величиной, которая подчиняется экспоненциальному закону распределения с параметром μ.Расчетные формулы
Вероятность того, что все каналы свободны
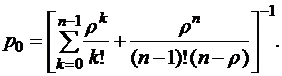
Вероятность того, что занято kканалов, при условии, что общее число заявок, находящихся на обслуживании, не превосходит числа каналов,
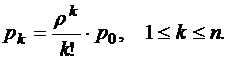
Вероятность того, что в системе находится k заявок, в случае, когда их число больше числа каналов,
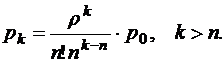
Вероятность того, что все каналы заняты,
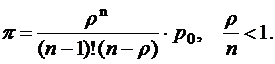
Среднее время ожидания заявкой начала обслуживания в системе
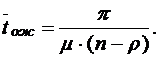
Средняя длина очереди
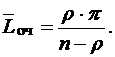
Среднее число свободных от обслуживания каналов
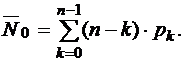
Автозаправочная станция с двумя колонками обслуживает пуассоновский поток машин с интенсивностью λ=0,8 машин в минуту. Время обслуживания одной машины подчиняется показательному закону со средним значением 2 минуты. В данном районе нет другой АЗС, так что очередь перед АЗС может расти практически неограниченно. Найдите:
1) среднее число занятых колонок;
2) вероятность отсутствия очереди у АЗС;
3) вероятность того, что придется ждать начала обслуживания;
4) среднее число машин в очереди;
5) среднее время ожидания в очереди;
6) среднее время пребывания машины на АЗС;
7) среднее число машин на АЗС.
Решение. По условию задачи n=2, λ=0.8; μ=1/tобсл=0.5; ρ=λ/μ=1.6
Поскольку ρ/n=0,8<1, то очередь не растет безгранично и имеет смысл говорить о предельном стационарном режиме работы системы массового обслуживания.
Находим вероятности состояний СМО:
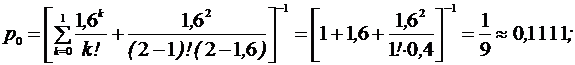
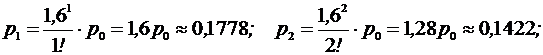
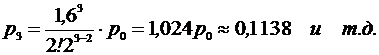
Среднее число занятых колонок:
Nзан=n-N0 = 2-(2·p0+1·p1) = 2-2·0.1111 - 0.1778 = 1.6
Вероятность отсутствия очереди у АЗС:
p0+p1+p2 = 0.1111+0.1778+0.1422 = 0.4311
Вероятность того, что придется ждать начала обслуживания равна вероятности того, что все колонки заняты:
p0+p1+p2 = 0.1111+0.1778+0.1422 = 0.4311
Среднее число машин в очереди:
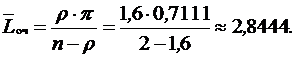
Среднее время ожидания в очереди:
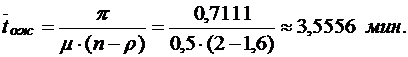
Среднее время пребывания машины на АЗС:
tпреб=tобсл+tож = 2+3.5556 = 5.5556 мин.
Среднее число машин на АЗС:
Nзан+Lоч = 1.6+2.8444 = 4.4444
Рассмотрим одноканальную СМО с ожиданиями, в которой число каналов равно единице n = 1, интенсивность поступления заявок – λ, интенсивность обслуживания равна μ. Заявка, поступившая в тот момент времени, когда канал занят, становится в очередь и ждет обслуживания. Количество мест в очереди ограничено и равно m. Если все места в очереди заняты, то заявка покидает очередь не обслуженной. Проанализируем состояние системы:
- S0 – канал свободен;
- S1 – канал занят;
- S2 – канал занят, одна заявка в очереди;
- Sk – канал занят, (k–1) заявок в очереди;
- Sm + 1 – канал занят, в очереди m заявок.
Изобразим граф состояний такой СМО (рис. 25).
Рис. 25
По формулам Эрланга найдем вероятности событий, состоящих в том, что СМО находится в состоянии S1, S2, …, Sm+1:
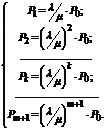 (28)
(28)
При этом вероятность того, что заявка, прибывшая в систему, найдет ее свободной, равна
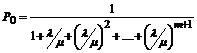 . (29)
. (29)
Отношение интенсивности поступления заявок λ к интенсивности обслуживания заявок μ есть приведенная интенсивность μ, т.е.
ρ=λ/μ
Произведем замену в формулах (28) и (29) отношения λ/&mu на ρ, тогда выражения примут вид:
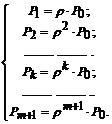 (30)
(30)
Вероятность Р0 будет вычисляться по следующей формуле:
p0=[1+ρ+ρ2+ ... +ρm+1]-1. (31)
Выражение для вероятности P0 есть геометрическая прогрессия, сумма которой будет равна
![]() .
.
Таким образом, формулы (30) и (31) позволяют определить вероятность любого события, которое может произойти в системе, т. е. определить вероятность нахождения системы в любом состоянии.
Формула для P0 справедлива для случая, когда ρ ≠ 1. В случае, когда ρ = 1, т. е. интенсивность поступления заявок равна интенсивности их обслуживания, используется другая формула для вычисления вероятности того, что система свободна:
![]() ,
,
где m – это количество заявок, находящихся в очереди.
Определим характеристики эффективности одноканальной СМО:
- вероятность того, что очередная заявка, прибывшая в систему, получит отказ Ротк;
- абсолютную пропускную способность А,
- относительную пропускную способность Q,
- число занятых каналов k,
- среднее число заявок в очереди r,
- среднее число заявок, связанных с СМО, z.
Очередная заявка, поступившая в систему, получает отказ в том случае, когда занят канал, т. е. идет обслуживание другой заявки, и все m мест в очереди также заняты. тогда вероятность этого события можно вычислить по следующей формуле:
![]() . (32)
. (32)
Вероятность того, что заявка придет в систему и либо немедленно будет обслужена, либо будут места в очереди, т. е. относительную пропускную способность, можно найти по формуле
![]() . (33)
. (33)
Среднее число заявок, которые могут быть обслужены в единицу времени, т. е. абсолютную пропускную способность, рассчитывают следующим образом:
A=Q·λ (34)
Таким образом, по формулам (32), (33), (34) можно вычислить основные показатели эффективности для любой системы массового обслуживания. теперь выведем выражения для вычисления характеристик, присущих лишь данной СМО.
Среднее число заявок в очереди r определим как математическое ожидание дискретной случайной величины, где R – число заявок в очереди.
♦ Р2 – это вероятность того, что в очереди на обслуживание находится одна заявка;
♦ Р3 – вероятность того, что в очереди две заявки;
♦ Рk – вероятность того, что в очереди (k–1) заявка;
♦ Рm + 1 – вероятность того что в очереди m заявок.
Тогда среднее число заявок в очереди можно вычислить следующим образом:
r=1·P2+2·P3+ ... +(k-1)·Pk+ ... +m·Pm+1. (35)
Подставим в формулу (35) найденные ранее значения вероятностей, вычисленные в формуле (30):
r=1·ρ2·p0+2·ρ3·p0+ ... +(k-1)·ρk·p0+ ... +m·ρm+1·p0. (35)
Вынесем за скобку вероятность P0 и Р2, тогда получим итоговую формулу для вычисления среднего числа заявок в очереди на обслуживание:
r=ρ2·p0(1+2·ρ+ ... +(k-1)·ρk-2+ ... +m·ρm-1)
Выведем формулу для среднего числа заявок, связанных с СМО, z, т. е. число заявок в очереди, находящихся на обслуживании. Рассмотрим общее число заявок, связанных с СМО, z как сумму двух величин среднего числа заявок в очереди r и числа занятых каналов k:
z = r+k.
Так как канал один, то число занятых каналов k может принимать значения 0 или 1. Вероятность того, что k = 0, т.е. система свободна, соответствует вероятности Р0, значение которой можно найти по формуле (31). Если k= 1, т.е. канал занят обслуживанием заявки, но места в очереди еще есть, то вероятность этого события можно вычислить по формуле
![]() .
.
Следовательно, z будет равно:
![]() . (37)
. (37)
Одноканальная СМО с ожиданием
Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью l. Интенсивность потока обслуживания равна m (т. е. в среднем непрерывно занятый канал будет выдавать m. обслуженных заявок). Длительность обслуживания — случайная величина, подчиненная показательному закону распределения. Поток обслуживании является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N-требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость.
Граф состояний СМО в этом случае имеет вид, показанный на Рис. 3.2.

Граф состояний одноканальной СМО с ожиданием (схема гибели и размножения)
Состояния СМО имеют следующую интерпретацию:
S0 - канал свободен
S1 - канал занят (очереди нет);
S2 - канал занят (одна заявка стоит в очереди);
………………………………
Sn-канал занят (n - 1 заявок стоит в очереди);
……………………………
SN - канал занят (N - 1 заявок стоит в очереди).
Стационарный провес в данной системе будет описываться следующей системой алгебраических уравнений:
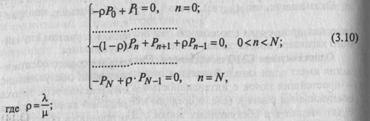
п -номер состояния.
Решение приведенной выше системы уравнений (3.10) для нашей модели СМО имеет вид
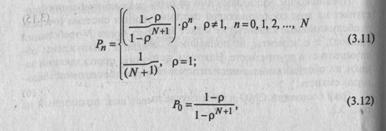
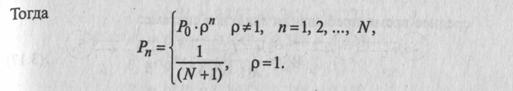
Следует отметить, что выполнение условия стационарности
l/m = p
Определим характеристики одноканальной СМОс ожиданием и ограниченной длиной очереди, равной (N —1):
- вероятность отказа в обслуживании заявки:

- среднее время пребывания заявки в системе:
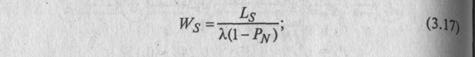
- средняя продолжительность пребывания клиента (заявки) в очереди:
Wq=WS-1/μ - среднее число заявок (клиентов) в очереди (длина очереди):
Lq=λ(1-PN)·Wq
Рассмотрим пример одноканальной СМО с ожиданием.
Пример 3.2. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограничено и равно 3 [(N- 1) = 3]. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность l= 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.
Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.
Решение
1. Параметр потока обслуживании автомобилей:
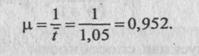
2. Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей l и m, т. е.
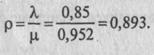
3. Вычислим финальные вероятности системы:
P1=ρ·P0 = 0.893·0.248 = 0.221
P2=ρ2·P0 = 0.8932·0.248 = 0.198
P3=ρ3·P0 = 0.8933·0.248 = 0.177
P4=ρ4·P0 = 0.8932·0.248 = 0.158
4. Вероятность отказа в обслуживании автомобиля:
Pотк=P4=ρ4·P0 ≈ 0.158
5. Относительная пропускная способность поста диагностики:
q=1-Pотк = 1-0.158 = 0.842
6. Абсолютная пропускная способность поста диагностики
A=λ·q = 0.85·0.842 = 0.716 (автомобиля в час)
7. Среднее число автомобилей, находящихся на обслуживании и в очереди (т.е. в системе массового обслуживания):
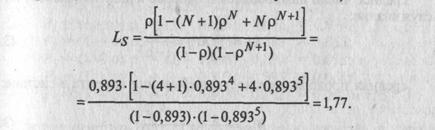
8. Среднее время пребывания автомобиля в системе:
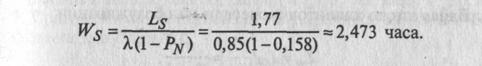
9. Средняя продолжительность пребывания заявки в очереди на обслуживание:
Wq=WS-1/μ = 2.473-1/0.952 = 1.423 часа
10. Среднее число заявок в очереди (длина очереди): Lq= А,(1 - PN) Wq= 0,85
Lq=λ(1-PN)·Wq = 0.85·(1-0.158)·1.423 = 1.02
Работу рассмотренного поста диагностики можно считать удовлетворительной, так как пост диагностики не обслуживает автомобили в среднем в 15,8% случаев (Ротк= 0,158). В качестве показателей эффективности СМО с ожиданием, кроме уже известных показателей — абсолютной А и относительной Q пропускной способности, вероятности отказа Pотк., среднего числа занятых каналов
Одноканальная система с неограниченной очередью
На практике часто встречаются одноканальные СМО с неограниченной очередью (например, телефон-автомат с одной будкой).Рассмотрим задачу.
Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживании — интенсивность μ. Необходимо найти предельные вероятности состояний и показатели эффективности СМО.
Система может находиться в одном из состояний S0, S1, S2, …, Sk, по числу заявок, находящихся в СМО: S0 — канал свободен; S1 — канал занят (обслуживает заявку), очереди нет, S2 — канал занят, одна заявка стоит в очереди; ... Sk — канал занят, (k—1) заявок стоят в очереди и т.д.
Граф состояний СМО представлен на рис. 8.

Рис. 8
Это процесс гибели и размножения, но с бесконечным числом состояний, в котором интенсивность потока заявок равна λ, а интенсивность потока обслуживании μ.
Прежде чем записать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время t→∞, очередь может неограниченно возрастать. Доказано, что если ρ<1, т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ≥1, очередь растет до бесконечности.
Для определения предельных вероятностей состояний воспользуемся формулами (16), (17) для процесса гибели и размножении (здесь мы допускаем известную нестрогость, так как ранее эти формулы были получены для случая конечного числа состояний системы). Получим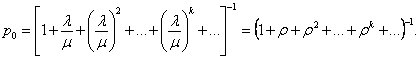 (32)
(32)
Так как предельные вероятности существуют лишь при ρ < 1, то геометрический ряд со знаменателем
ρ < 1, записанный в скобках в формуле (32), сходится к сумме, равной ![]() . Поэтому
. Поэтому
p0=1-ρ, (33)
и с учетом соотношений (17)
p1=ρ·p0; p2=ρ2·p0; ... ; pk=ρk·p0; ...
найдем предельные вероятности других состояний
p1=ρ·(1-ρ); p2=ρ2·(1-ρ); ... ; pk=ρk·(1-ρ); ... (34)
Предельные вероятности p0, p1, p2, …, pk,… образуют убывающую геометрическую профессию со знаменателем р < 1, следовательно, вероятность р0 — наибольшая. Это означает, что если СМО справляется с потоком заявок (при ρ < 1), то наиболее вероятным будет отсутствие заявок в системе.
Среднее число заявок в системе Lсист. определим по формуле математического ожидания, которая с учетом (34) примет вид
![]() (35)
(35)
(суммирование от 1 до ∞, так как нулевой член 0·p0=0).
Можно показать, что формула (35) преобразуется (при ρ < 1) к виду
![]() (36)
(36)
Найдем среднее число заявок в очереди Lоч. Очевидно, что
Lоч=Lсист-Lоб (37)
где Lоб. — среднее число заявок, находящихся под обслуживанием.
Среднее число заявок под обслуживанием определим по формуле математического ожидания числа заявок под обслуживанием, принимающего значения 0 (если канал свободен) либо 1 (если канал занят):
Lоч=0·p0+1·(1-p0)
т.е. среднее число заявок под обслуживанием равно вероятности того, что канал занят:
Lоч=Pзан=1-p0, (38)
В силу (33)
Lоч=Pзанρ, (39)
Теперь по формуле (37) с учетом (36) и (39)
![]() (40)
(40)
Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (в очереди), деленному на интенсивность потока заявок, т.е.
![]() (41)
(41)
![]() (42)
(42)
Формулы (41) и (42) называются формулами Литтла.
Они вытекают из того, что в предельном, стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих
ее: оба потока заявок имеют одну и ту же интенсивность λ.
На основании формул (41) и (42) с учетом (36) и (40) среднее время пребывания заявки в системе определится по формуле:
![]() (43)
(43)
а среднее время пребывания заявки в очереди
![]() (44)
(44)
Одноканальная СМО с ожиданием без ограничения на вместимость блока ожидания
Стационарный режим функционирования данной СМО существует при t→∞ для любого п=0,1,2,… и когда l < m.Система алгебраических уравнений, описывающих работу СМО при t®¥ для любого n = 0, 1, 2...., имеет вид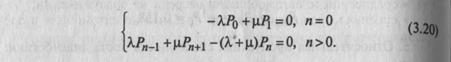
Решение данной системы уравнений имеет вид
Pn=(1-ρ)·ρn, n=0,1,2,... (3.21)
где ρ=λ/μ < 1
Характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди, следующие:
среднее число находящихся в системе клиентов (заявок) на обслуживание:
средняя продолжительность пребывания клиента в системе:
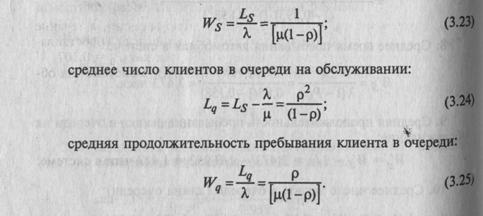
Пример 3.3. Вспомним о ситуации, рассмотренной в пример 3.2, где речь идет о функционировании поста диагностики. Пусть рассматриваемый пост диагностики располагает неограниченны» количеством площадок для стоянки прибывающих на обслуживание автомобилей, т. е. длина очереди не ограничена.
Требуется определить финальные значения следующих вероятностных характеристик:
- вероятности состояний системы (поста диагностики);
- среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);
- среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);
- среднее число автомобилей в очереди на обслуживании;
- среднюю продолжительность пребывания автомобиля в очереди.
Решение
1. Параметр потока обслуживания m и приведенная интенсивность потока автомобилей р определены в примере 3.2:
m = 0,952; p = 0,893.
2. Вычислим предельные вероятности системы по формулам
P0=1-ρ = 1-0.893 = 0.107
P1=(1-ρ)·ρ = (1-0.893)·0.893 = 0.096
P2=(1-ρ)·ρ2 = (1-0.893)2·0.893 = 0.085
P3=(1-ρ)·ρ3 = (1-0.893)3·0.893 = 0.076
P4=(1-ρ)·ρ4 = (1-0.893)4·0.893 = 0.068
P5=(1-ρ)·ρ5 = (1-0.893)5·0.893 = 0.061
и т.д.
Следует отметить, что Ро определяет долю времени, в течение которого пост диагностики вынужденно бездействует (простаивает). В нашем примере она составляет 10,7%, так как Ро= 0,107.
3. Среднее число автомобилей, находящихся в системе (на обслуживании и в очереди):
4. Средняя продолжительность пребывания клиента в системе:

6. Средняя продолжительность пребывания автомобиля в очереди-
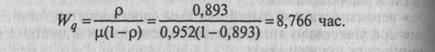
7. Относительная пропускная способность системы:
т. е. каждая заявка, пришедшая в систему, будет обслужена.
8. Абсолютная пропускная способность: А= lq= 0,85·1 = 0,85
Следует отметить, что предприятие, осуществляющее диагностику автомобилей, прежде всего интересует количество клиентов, которое посетит пост диагностики при снятии ограничения на длину очереди.
Допустим, в первоначальном варианте количество мест для стоянки прибывающих автомобилей было равно трем (см. пример 3.2). Частота m возникновения ситуаций, когда прибывающий на пост диагностики автомобиль не имеет возможности присоединиться к очереди:
m = l Рор4 = 0,85·0,248·0,8934·0,134 автомобиля в час.
При 12-часовом режиме работы поста диагностики это эквивалентно тому, что пост диагностики в среднем за смену (день) будет терять 12·0,134 = 1,6 автомобиля.
Снятие ограничения на длину очереди позволяет увеличить количество обслуженных клиентов в нашем примере в среднем на 1,6 автомобиля за смену (12 ч. работы) поста диагностики. Ясно, что решение относительно расширения площади для стоянки автомобилей, прибывающих на пост диагностики, должно основываться на оценке экономического ущерба, который обусловлен потерей клиентов при наличии всего трех мест для стоянки этих автомобилей.
Многоканальная СМО с неограниченной очередью
Рассмотрим задачу. Имеется n-канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживании — интенсивность μ. Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.Система может находиться в одном из состояний S0, S1, S2,…, Sk,…, Sn,…, — нумеруемых по числу заявок, находящихся в СМО: S0 — в системе нет заявок (все каналы свободны); S1 — занят один канал, остальные свободны; S2 — заняты два канала, остальные свободны;..., Sk — занято k каналов, остальные свободны;..., Sn — заняты все n каналов (очереди нет); Sn+1 — заняты все n каналов, в очереди одна заявка;..., Sn+r — заняты все n каналов, r заявок стоит в очереди,....
Граф состояний системы показан на рис. 9. Обратим внимание на то, что в отличие от предыдущей СМО, интенсивность потока обслуживаний (переводящего систему из одного состояния в другое справа налево) не остается постоянной, а по мере увеличения числа заявок в СМО от 0 до n увеличивается от величины m до nm, так как соответственно увеличивается число каналов обслуживания. При числе заявок в СМО большем, чем n, интенсивность потока обслуживании сохраняется равной nm.
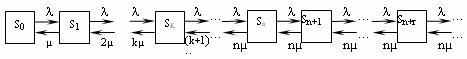
Рис. 9
Можно показать, что при r/n < 1 предельные вероятности существуют. Если r/n > 1, очередь растет до бесконечности. Используя формулы (16) и (17) для процесса гибели и размножения, можно получить следующие формулы для предельных вероятностей состояний n-канальной СМО с неограниченной очередью
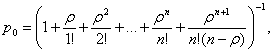 , (45)
, (45)
Вероятность того, что заявка окажется в очереди,
Для n-канальной СМО с неограниченной очередью, используя прежние приемы, можно найти:
среднее число занятых каналов
среднее число заявок в очереди
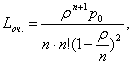 , (50)
, (50)
среднее число заявок в системе
Lсист=Lоч+ρ, (51)
Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе, как и ранее, находятся по формулам Литтла (42) и (41).
Замечание. Для СМО с неограниченной очередью при r < 1 любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа Pотк = 0, относительная пропускная способность Q=1, а абсолютная пропускная способность равна интенсивности входящего потока заявок, т.е. А=l.
СМО с ограниченной очередью
СМО с ограниченной очередью. СМО с ограниченной очередью отличаются от рассмотренных выше задач лишь тем, что число заявок в очереди ограничено (не может превосходить некоторого заданного т). Если новая заявка поступает в момент, когда все места в очереди заняты, она покидает СМО необслуженной, т.е. получает отказ.Очевидно: для вычисления предельных вероятностей состояний и показателей эффективности таких СМО может быть использован тот же подход, что и выше, с той разницей, что суммировать надо не бесконечную прогрессию (как, например, мы делали при выводе формулы (33)), а конечную.
Среднее время пребывания заявки в очереди и в системе, как и ранее, определяем по формулам Литтла (44) и (43).
СМО с ограниченным временем ожидания. На практике часто встречаются СМО с так называемыми "нетерпеливыми" заявками. Такие заявки могут уйти из очереди, если время ожидания превышает некоторую величину. В частности, такого рода заявки возникают в различных технологических системах, в которых задержка с началом обслуживания может привести к потере качества продукции, в системах оперативного управления, когда срочные сообщения теряют ценность (или даже смысл), если они не поступают на обслуживание в течение определенного времени.
В простейших математических моделях таких систем предполагается, что заявка может находиться в очереди случайное время, распределенное по показательному закону с некоторым параметром υ, т.е. можно условно считать, что каждая заявка, стоящая в очереди на обслуживание, может покинуть систему с интенсивностью υ.
Соответствующие показатели эффективности СМО с ограниченным временем получаются на базе результатов, полученных для процесса гибели и размножения.
В заключение отметим, что на практике часто встречаются замкнутые системы обслуживания, у которых входящий поток заявок существенным образом зависит от состояния самой СМО. В качестве примера можно привести ситуацию, когда на ремонтную базу поступают с мест эксплуатации некоторые машины: понятно, что чем больше машин находится в состоянии ремонта, тем меньше их продолжает эксплуатироваться и тем меньше интенсивность потока вновь поступающих на ремонт машин. Для замкнутых СМО характерным является ограниченное число источников заявок, причем каждый источник "блокируется" на время обслуживания его заявки (т.е. он не выдает новых заявок). В подобных системах при конечном числе состояний СМО предельные вероятности будут существовать при любых значениях интенсивностей потоков заявок и обслуживании. Они могут быть вычислены, если вновь обратиться к процессу гибели и размножения.