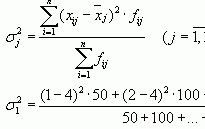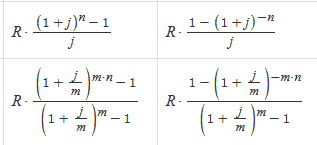Проверка гипотезы о нормальном распределении
Критерий согласия Пирсона:Проверить гипотезу о нормальном распределении по критерию Пирсона. Уровень значимости α=0.05. Данные разбить на 6 интервалов.
Решение находим с помощью калькулятора. Ширина интервала составит: 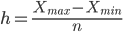
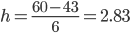
Xmax - максимальное значение группировочного признака в совокупности.
Xmin - минимальное значение группировочного признака.
Определим границы группы.
| Номер группы | Нижняя граница | Верхняя граница |
| 1 | 43 | 45.83 |
| 2 | 45.83 | 48.66 |
| 3 | 48.66 | 51.49 |
| 4 | 51.49 | 54.32 |
| 5 | 54.32 | 57.15 |
| 6 | 57.15 | 60 |
Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп.
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| 43 | 43 - 45.83 | 1 |
| 48.5 | 45.83 - 48.66 | 1 |
| 49 | 48.66 - 51.49 | 1 |
| 49 | 48.66 - 51.49 | 2 |
| 49.5 | 48.66 - 51.49 | 3 |
| 50 | 48.66 - 51.49 | 4 |
| 50 | 48.66 - 51.49 | 5 |
| 50.5 | 48.66 - 51.49 | 6 |
| 51.5 | 51.49 - 54.32 | 1 |
| 51.5 | 51.49 - 54.32 | 2 |
| 52 | 51.49 - 54.32 | 3 |
| 52 | 51.49 - 54.32 | 4 |
| 52 | 51.49 - 54.32 | 5 |
| 52 | 51.49 - 54.32 | 6 |
| 52 | 51.49 - 54.32 | 7 |
| 52 | 51.49 - 54.32 | 8 |
| 52 | 51.49 - 54.32 | 9 |
| 52.5 | 51.49 - 54.32 | 10 |
| 52.5 | 51.49 - 54.32 | 11 |
| 53 | 51.49 - 54.32 | 12 |
| 53 | 51.49 - 54.32 | 13 |
| 53 | 51.49 - 54.32 | 14 |
| 53.5 | 51.49 - 54.32 | 15 |
| 54 | 51.49 - 54.32 | 16 |
| 54 | 51.49 - 54.32 | 17 |
| 54 | 51.49 - 54.32 | 18 |
| 54.5 | 54.32 - 57.15 | 1 |
| 54.5 | 54.32 - 57.15 | 2 |
| 55.5 | 54.32 - 57.15 | 3 |
| 57 | 54.32 - 57.15 | 4 |
| 57.5 | 57.15 - 59.98 | 1 |
| 57.5 | 57.15 - 59.98 | 2 |
| 58 | 57.15 - 59.98 | 3 |
| 58 | 57.15 - 59.98 | 4 |
| 58.5 | 57.15 - 59.98 | 5 |
| 60 | 57.15 - 59.98 | 6 |
| Группы | № совокупности | Частота fi |
| 43 - 45.83 | 1 | 1 |
| 45.83 - 48.66 | 2 | 1 |
| 48.66 - 51.49 | 3,4,5,6,7,8 | 6 |
| 51.49 - 54.32 | 9,10,11,12,13,14,15, 16,17,18,19,20,21, 22,23,24,25,26 | 18 |
| 54.32 - 57.15 | 27,28,29,30 | 4 |
| 57.15 - 59.98 | 31,32,33,34,35,36 | 6 |
| Группы | xi | Кол-во, fi | xi * fi | Накопленная частота, S | |x - xср|*f | (x - xср)2*f | Частота, fi/n |
| 43 - 45.83 | 44.42 | 1 | 44.42 | 1 | 8.88 | 78.91 | 0.0278 |
| 45.83 - 48.66 | 47.25 | 1 | 47.25 | 2 | 6.05 | 36.64 | 0.0278 |
| 48.66 - 51.49 | 50.08 | 6 | 300.45 | 8 | 19.34 | 62.33 | 0.17 |
| 51.49 - 54.32 | 52.91 | 18 | 952.29 | 26 | 7.07 | 2.78 | 0.5 |
| 54.32 - 57.15 | 55.74 | 4 | 222.94 | 30 | 9.75 | 23.75 | 0.11 |
| 57.15 - 59.98 | 58.57 | 6 | 351.39 | 36 | 31.6 | 166.44 | 0.17 |
| 36 | 1918.73 | 82.7 | 370.86 | 1 |
Показатели центра распределения.
Средняя взвешенная
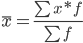
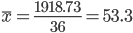
Мода
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
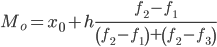
где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота.
Выбираем в качестве начала интервала 51.49, так как именно на этот интервал приходится наибольшее количество.
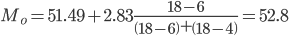
Наиболее часто встречающееся значение ряда – 52.8
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.
В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 51.49 - 54.32, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
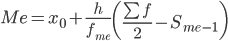
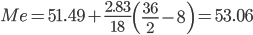
Таким образом, 50% единиц совокупности будут меньше по величине 53.06
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 60 - 43 = 17
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.
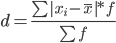
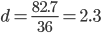
Каждое значение ряда отличается от другого не более, чем на 2.3
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
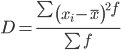
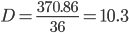
Несмещенная оценка дисперсии - состоятельная оценка дисперсии.
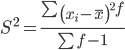
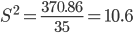
Среднее квадратическое отклонение.
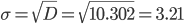
Каждое значение ряда отличается от среднего значения 53.3 не более, чем на 3.21
Оценка среднеквадратического отклонения.
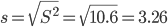
Относительные показатели вариации.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
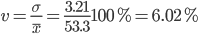
Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.
Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.
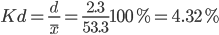
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
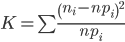
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
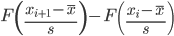
где s = 3.21, xср = 53.3
Теоретическая (ожидаемая) частота равна ni = npi, где n = 36
| Интервалы группировки | Наблюдаемая частота ni | x1 = (xi-x)/s | x2 = (xi+1-x)/s | Ф(x1) | Ф(x2) | Вероятность попадания в i-й интервал, pi = Ф(x2) - Ф(x1) | Ожидаемая частота, 36pi | Слагаемые статистики Пирсона, Ki |
| 43 - 45.83 | 1 | -3.16 | -2.29 | -0.5 | -0.49 | 0.01 | 0.36 | 1.14 |
| 45.83 - 48.66 | 1 | -2.29 | -1.42 | -0.49 | -0.42 | 0.0657 | 2.37 | 0.79 |
| 48.66 - 51.49 | 6 | -1.42 | -0.56 | -0.42 | -0.21 | 0.21 | 7.61 | 0.34 |
| 51.49 - 54.32 | 18 | -0.56 | 0.31 | -0.21 | 0.13 | 0.34 | 12.16 | 2.8 |
| 54.32 - 57.15 | 4 | 0.31 | 1.18 | 0.13 | 0.38 | 0.26 | 9.27 | 3 |
| 57.15 - 59.98 | 6 | 1.18 | 2.06 | 0.38 | 0.48 | 0.0973 | 3.5 | 1.78 |
| 36 | 9.84 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).
Kkp = 7.81473; Kнабл = 9.84
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по нормальному закону.
Перейти к онлайн решению своей задачи
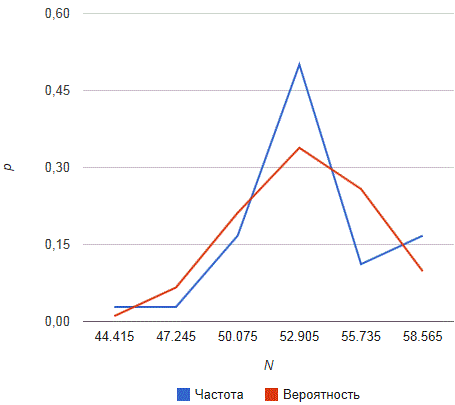
Пример №2. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение находим с помощью калькулятора.
Таблица для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)·f | (x-x)2·f | (x-x)3·f | Частота, fi/n |
| 5 | 15 | 75 | 15 | 114.45 | 873.25 | -6662.92 | 0.075 |
| 7 | 26 | 182 | 41 | 146.38 | 824.12 | -4639.79 | 0.13 |
| 9 | 25 | 225 | 66 | 90.75 | 329.42 | -1195.8 | 0.13 |
| 11 | 30 | 330 | 96 | 48.9 | 79.71 | -129.92 | 0.15 |
| 13 | 26 | 338 | 122 | 9.62 | 3.56 | 1.32 | 0.13 |
| 15 | 21 | 315 | 143 | 49.77 | 117.95 | 279.55 | 0.11 |
| 17 | 24 | 408 | 167 | 104.88 | 458.33 | 2002.88 | 0.12 |
| 19 | 20 | 380 | 187 | 127.4 | 811.54 | 5169.5 | 0.1 |
| 21 | 13 | 273 | 200 | 108.81 | 910.74 | 7622.89 | 0.065 |
| 200 | 2526 | 800.96 | 4408.62 | 2447.7 | 1 |
Средняя взвешенная
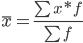
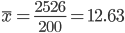
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 21 - 5 = 16
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
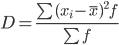
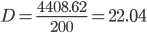
Несмещенная оценка дисперсии - состоятельная оценка дисперсии.
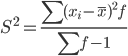
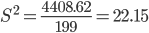
Среднее квадратическое отклонение.
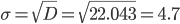
Каждое значение ряда отличается от среднего значения 12.63 не более, чем на 4.7
Оценка среднеквадратического отклонения.
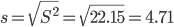
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
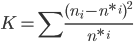
где n*i - теоретические частоты:
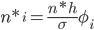
Вычислим теоретические частоты, учитывая, что:
n = 200, h=2 (ширина интервала), σ = 4.7, xср = 12.63
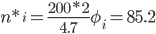
| i | xi | ui | φi | n*i |
| 1 | 5 | -1.63 | 0,1057 | 9.01 |
| 2 | 7 | -1.2 | 0,1942 | 16.55 |
| 3 | 9 | -0.77 | 0,2943 | 25.07 |
| 4 | 11 | -0.35 | 0,3752 | 31.97 |
| 5 | 13 | 0.0788 | 0,3977 | 33.88 |
| 6 | 15 | 0.5 | 0,3503 | 29.84 |
| 7 | 17 | 0.93 | 0,2565 | 21.85 |
| 8 | 19 | 1.36 | 0,1582 | 13.48 |
| 9 | 21 | 1.78 | 0,0804 | 6.85 |
Χ2=
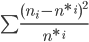
| i | ni | n*i | ni-n*i | (ni-n*i)2 | (ni-n*i)2/n*i |
| 1 | 15 | 9.01 | -5.99 | 35.94 | 3.99 |
| 2 | 26 | 16.55 | -9.45 | 89.39 | 5.4 |
| 3 | 25 | 25.07 | 0.0734 | 0.00539 | 0.000215 |
| 4 | 30 | 31.97 | 1.97 | 3.86 | 0.12 |
| 5 | 26 | 33.88 | 7.88 | 62.14 | 1.83 |
| 6 | 21 | 29.84 | 8.84 | 78.22 | 2.62 |
| 7 | 24 | 21.85 | -2.15 | 4.61 | 0.21 |
| 8 | 20 | 13.48 | -6.52 | 42.53 | 3.16 |
| 9 | 13 | 6.85 | -6.15 | 37.82 | 5.52 |
| ∑ | 200 | 200 | 22.86 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям σ, k = 9, r=2 (параметры xcp и σ оценены по выборке).
Kkp(0.05;6) = 12.59159; Kнабл = 22.86
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по нормальному закону. Другими словами, эмпирические и теоретические частоты различаются значимо.
Пример 2. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение.
Таблица для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)·f | (x-x)2·f | (x-x)3·f | Частота, fi/n |
| 0.3 | 6 | 1.8 | 6 | 5.77 | 5.55 | -5.34 | 0.03 |
| 0.5 | 9 | 4.5 | 15 | 6.86 | 5.23 | -3.98 | 0.045 |
| 0.7 | 26 | 18.2 | 41 | 14.61 | 8.21 | -4.62 | 0.13 |
| 0.9 | 25 | 22.5 | 66 | 9.05 | 3.28 | -1.19 | 0.13 |
| 1.1 | 30 | 33 | 96 | 4.86 | 0.79 | -0.13 | 0.15 |
| 1.3 | 26 | 33.8 | 122 | 0.99 | 0.0375 | 0.00143 | 0.13 |
| 1.5 | 21 | 31.5 | 143 | 5 | 1.19 | 0.28 | 0.11 |
| 1.7 | 24 | 40.8 | 167 | 10.51 | 4.6 | 2.02 | 0.12 |
| 1.9 | 20 | 38 | 187 | 12.76 | 8.14 | 5.19 | 0.1 |
| 2.1 | 8 | 16.8 | 195 | 6.7 | 5.62 | 4.71 | 0.04 |
| 2.3 | 5 | 11.5 | 200 | 5.19 | 5.39 | 5.59 | 0.025 |
| 200 | 252.4 | 82.3 | 48.03 | 2.54 | 1 |
Средняя взвешенная
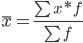
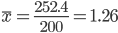
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 2.3 - 0.3 = 2
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
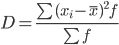
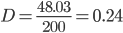
Несмещенная оценка дисперсии - состоятельная оценка дисперсии.
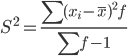
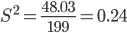
Среднее квадратическое отклонение.
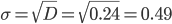
Каждое значение ряда отличается от среднего значения 1.26 не более, чем на 0.49
Оценка среднеквадратического отклонения.
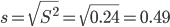
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
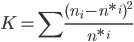
где n*i - теоретические частоты:
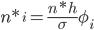
Вычислим теоретические частоты, учитывая, что:
n = 200, h=0.2 (ширина интервала), σ = 0.49, xср = 1.26
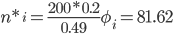
| i | xi | ui | φi | n*i |
| 1 | 0.3 | -1.96 | 0,0573 | 4.68 |
| 2 | 0.5 | -1.55 | 0,1182 | 9.65 |
| 3 | 0.7 | -1.15 | 0,2059 | 16.81 |
| 4 | 0.9 | -0.74 | 0,3034 | 24.76 |
| 5 | 1.1 | -0.33 | 0,3765 | 30.73 |
| 6 | 1.3 | 0.0775 | 0,3977 | 32.46 |
| 7 | 1.5 | 0.49 | 0,3538 | 28.88 |
| 8 | 1.7 | 0.89 | 0,2661 | 21.72 |
| 9 | 1.9 | 1.3 | 0,1691 | 13.8 |
| 10 | 2.1 | 1.71 | 0,0909 | 7.42 |
| 11 | 2.3 | 2.12 | 0,0422 | 3.44 |
Χ2=
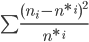
| i | ni | n*i | ni-n*i | (ni-n*i)2 | (ni-n*i)2/n*i |
| 1 | 6 | 4.68 | -1.32 | 1.75 | 0.37 |
| 2 | 9 | 9.65 | 0.65 | 0.42 | 0.0435 |
| 3 | 26 | 16.81 | -9.19 | 84.53 | 5.03 |
| 4 | 25 | 24.76 | -0.24 | 0.0555 | 0.00224 |
| 5 | 30 | 30.73 | 0.73 | 0.53 | 0.0174 |
| 6 | 26 | 32.46 | 6.46 | 41.75 | 1.29 |
| 7 | 21 | 28.88 | 7.88 | 62.07 | 2.15 |
| 8 | 24 | 21.72 | -2.28 | 5.2 | 0.24 |
| 9 | 20 | 13.8 | -6.2 | 38.41 | 2.78 |
| 10 | 8 | 7.42 | -0.58 | 0.34 | 0.0454 |
| 11 | 5 | 3.44 | -1.56 | 2.42 | 0.7 |
| ∑ | 200 | 200 | 12.67 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям σ, k = 11, r=2 (параметры xcp и σ оценены по выборке).
Kkp(0.05;8) = 15.50731; Kнабл = 12.67
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение.