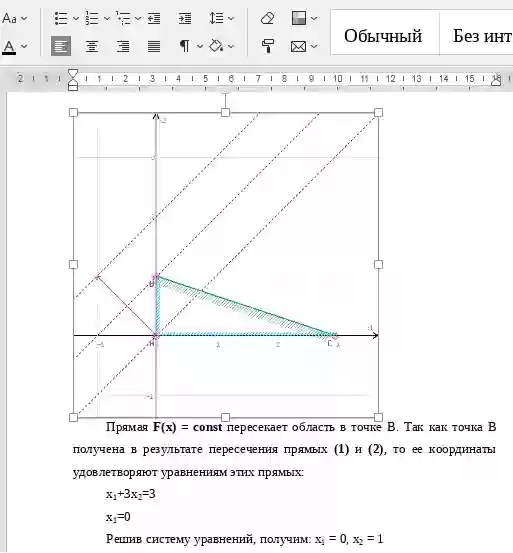
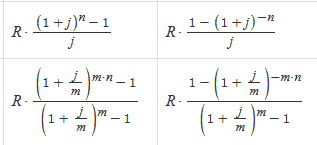Графический метод решения ЗЛП
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).Назначение сервиса. С помощью данного сервиса можно в онлайн режиме решить задачу линейного программирования геометрическим методом, а также получить решение двойственной задачи (оценить оптимальность использования ресурсов). Дополнительно создается шаблон решения в Excel.
1 ≤ x1 ≤ 4, то оно разбивается на два: x1 ≥ 1, x1 ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.
Симплексный метод решения ЗЛП
Решение транспортной задачи
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Вычисление пределов
Решение задачи линейного программирования графическим методом включает следующие этапы:
- На плоскости X10X2 строят прямые.
- Определяются полуплоскости.
- Определяют многоугольник решений;
- Строят вектор N(c1,c2), который указывает направление целевой функции;
- Передвигают прямую целевую функцию c1x2 + c2x2 = 0 в направлении вектора N до крайней точки многоугольника решений.
- Вычисляют координаты точки и значение целевой функции в этой точке.
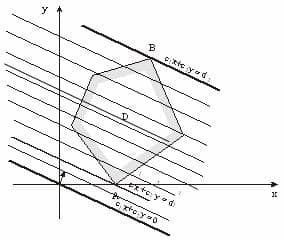
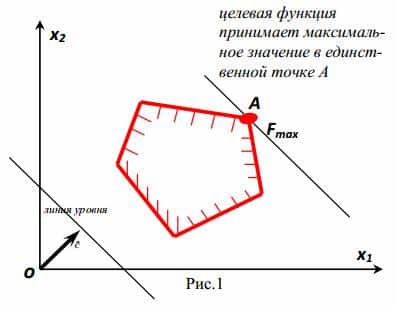
При этом могут возникать следующие ситуации:
- Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.
- Целевая функция принимает экстремальное значение в любой точке отрезка АВ.
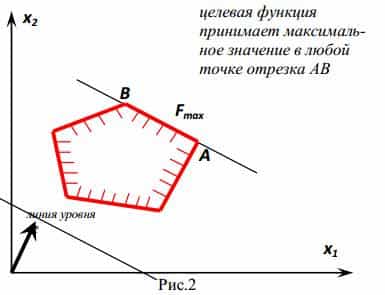
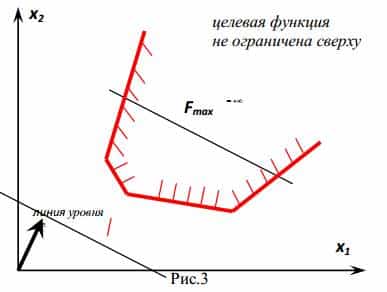
- Целевая функция не ограничена сверху (при поиске на максимум) или снизу (на минимум)
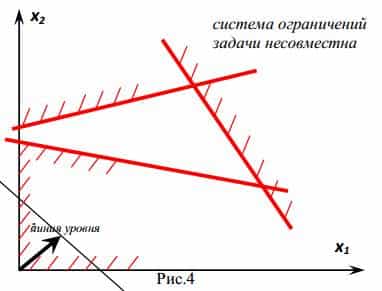
- Система ограничений задачи несовместна
Пример. Компания изготавливает два вида продукции – П1 и П2. Для производства продукции используются два вида сырья – С1 и С2. Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Таблица - Расход сырья на производство продукции
| Сырье | Расход сырья на 1 ед. продукции | Максимальный запас сырья, ед. | |
| П1 | П2 | ||
| М1 | 6 | 4 | 24 |
| М2 | 1 | 2 | 6 |
Требуется определить:
Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
- Сформулировать математическую модель задачи линейного программирования.
- Решить задачу линейного программирования графическим способом (для двух переменных).
Решение.
Сформулируем математическую модель задачи линейного программирования.
x1 – производство продукции П1, ед.
x2 – производство продукции П2, ед.
x1, x2 ≥ 0
Ограничения по ресурсам
6x1 + 4x2 ≤ 24
x1 + 2x2 ≤ 6
Ограничения по спросу
x1 +1 ≥ x2
x2 ≤ 2
Целевая функция
5x1 + 4x2 → max
Тогда получаем следующую ЗЛП:
6x1 + 4x2 ≤ 24
x1 + 2x2 ≤ 6
x2 - x1 ≤ 1
x2 ≤ 2
x1, x2 ≥ 0
5x1 + 4x2 → max
Примеры решения задачи линейного программирования графически.
Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x1 - 2x2 + 5x3 - 4x5 → max при ограничениях:
x1 + x2 + x3=12
2x1 - x2 + x4=8
- 2x1 + 2x2 + x5=10
F(X) = 3x1 - 2x2 + 5x3 - 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.
3. В качестве базовой переменной можно выбрать x5.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 - x2 + x4 = 8
- 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = - x1 - x2+12
x4 = - 2x1 + x2+8
x5 = 2x1 - 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 - 2x2 + 5(- x1 - x2+12) - 4(2x1 - 2x2+10)
или
F(X) = - 10x1 + x2+20 → max
Система неравенств:
- x1 - x2+12 ≥ 0
- 2x1 + x2+8 ≥ 0
2x1 - 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 - x2 ≤ 8
- 2x1 + 2x2 ≤ 10
F(X) = - 10x1 + x2+20 → max
Особенности решения задач линейного программирования графическим методом
Пример №1. Записать задачу в стандартной форме и решить ее графическим методом.f=x1+13x2-x3+2x4+3x5
-x2+x3-x5=-3
x1-4x2+3x3-x4+2x5=3
4x2-x3+x4-x5=6
Из первого уравнения выражаем x5:
x5 = -x2+x3+3
и подставим во все выражения:
f=x1+13x2-x3+2x4+3(-x2+x3+3)
x1-4x2+3x3-x4+2(-x2+x3+3)=3
4x2-x3+x4-(-x2+x3+3)=6
или
f=x1+10x2+2x3+2x4+9
x1-6x2+5x3-x4=-3
5x2-2x3+x4=9
Из второго уравнения выражаем x4:
x4=9-5x2+2x3
и подставим во все выражения:
f=x1+6x3+27
x1-x2+3x3=6
Переменную x2 принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x1 + 6x3+ 27
x1 + 3x3≥6
Далее задача решается графическом способом.
Пример №2
F(X) = 3x1 - 2x2 + 5x3 - 4x5 → max при ограничениях:
x1 + x2 + x3=12
2x1 - x2 + x4=8
- 2x1 + 2x2 + x5=10
F(X) = 3x1 - 2x2 + 5x3 - 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.
3. В качестве базовой переменной можно выбрать x5.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 - x2 + x4 = 8
- 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = - x1 - x2+12
x4 = - 2x1 + x2+8
x5 = 2x1 - 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 - 2x2 + 5(- x1 - x2+12) - 4(2x1 - 2x2+10)
или
F(X) = - 10x1 + x2+20 → max
Система неравенств:
- x1 - x2+12 ≥ 0
- 2x1 + x2+8 ≥ 0
2x1 - 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 - x2 ≤ 8
- 2x1 + 2x2 ≤ 10
F(X) = - 10x1 + x2+20 → max
Пример №3. Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
- Составить систему математических зависимостей (неравенств) и целевую функцию.
- Изобразить геометрическую интерпретацию задачи.
- Найти оптимальное решение.
- Провести аналитическую проверку.
- Определить существенные и несущественные ресурсы и их избытки.
- Определить значение целевой функции.
- Вычислить объективно обусловленные оценки.
- Составить соотношение устойчивости.
| Наимен. показат. | Нормы на одно изделие | Прибыль на одно изделие | ||
| Рес. 1 | Рес. 2 | Рес. 3 | ||
| Изделие 1 | 10.0 | 14.0 | 3.8 | 40 |
| Изделие 2 | 22.0 | 7.5 | 14.5 | 75 |
| Наличие ресурсов | 450 | 310 | 360 | - |