Метод Пауэлла полиномиальной аппроксимации
Этот метод основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации.Назначение сервиса. Онлайн-калькулятор предназначен для нахождения минимума функции методом Пауэлла (см. также калькулятор для двух переменных). Решение оформляется в формате Word.
Правила ввода функций:
Схема алгоритма Пауэлла
пусть x1 - начальная точка; Δx- выбранная величина шага по оси х.Шаг 1: Вычислить x2=x1+Δx.
Шаг 2: Вычислить f(x1) и f(x2).
Шаг 3: Если f(x1)>f(x2), положить x3=x1+2Δx, если f(x1)≤f(x2), то x3=x1-Δx.
Шаг 4: Вычислить f(x3) и найти Fmin = min{f1, f2, f3}
Xmin равно точке xi, которая соответствует Fmin.
Шаг 5: По трем точкам x1, x2, x3 вычислить x, используя квадратичную аппроксимацию.
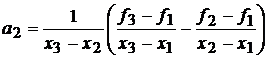
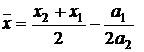
Шаг 6: Проверка на окончание поиска:
а) является ли разность |Fmin-f(z)|≤ε;
б) является ли разность |Xmin-x|≤δ,
где ε>0 и δ>0 - заданные точности.
Если условия а) и б) выполняются одновременно, то закончить поиск. Иначе переход на Шаг 7.
Шаг 7: Выбрать "наилучшую" точку (Xmin или x) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти на Шаг 4.
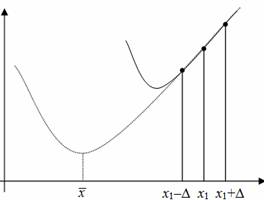
Замечание: после пятого шага необходимо провести дополнительную проверку, т.к. точка x может находиться за точкой x3. В этом случае точка x заменяется точкой, координата которой вычисляется c учетом заранее установленной длины шага.
Пусть полученная точка x лежит вне отрезка интерполяции. Смысл здесь заключается в следующем. О характере функции, в общем случае, ничего неизвестно, но при помощи аппроксимации происходит замена ее по трем точкам параболой (на рисунке обозначена пунктиром). Вид параболы полностью определяется выбранными точками. Если точки выбраны неудачно, то минимум параболы может оказаться весьма далеко от минимума функции. Причем, если у функции имеются несколько локальных минимумов, в итоге можно найти не тот минимум, что является ближайшим к начальной точке. Применение же вышеописанного правила предотвращает подобную ситуацию.
Пример. Найти ![]() .
.
Пусть начальная точка x1=1 и длина шага Δx=1.
Критерии останова:
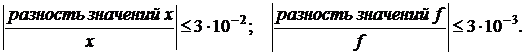
Итерация 1:
Шаг 1: x2=x1+ Δx =2
Шаг 2: f(x1)=18; f(x2)=16
Шаг 3: f(x1)>f(x2), следовательно x3=1+2 = 3;
Шаг 4: f(x3)=23.33;Fmin=16; Xmin=x2.
Шаг 5:
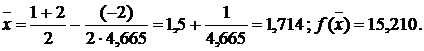
а)
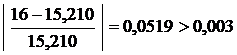 . Критерий останова не выполняется, следовательно поиск продолжается. Переход на Шаг 7.
. Критерий останова не выполняется, следовательно поиск продолжается. Переход на Шаг 7.
Шаг 7: Выбираем x как "наилучшую" точку, а x1=1, x2=2 – как точки, которые ее окружают. Обозначим эти точки в естественном порядке и переходим к Шагу 4.
Итерация 2:
Шаг 4: x1=1; f1=18; x2=1.714, f2=15.21 = Fmin;
Xmin = x2 = 1.714, x3= 2; f3 = 16
Шаг 5:
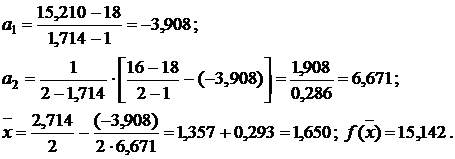
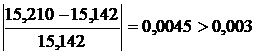 .
.
Первый критерий останова не выполняется. Переход на Шаг 7.
Шаг 7: Выбираем x как "наилучшую" точку, а x1 = 1, x2 = 1,714 – как точки, которые ее окружают. Обозначим эти точки в естественном порядке и переходим к Шагу 4.
Итерация 3:
Шаг 4:
x1 = 1, f1 = 18; x2 = 1.65; f2 = 15.142; = Fmin; Xmin= x2 = 1.65
x3 = 1.174; f3 = 15.21
Шаг 5:
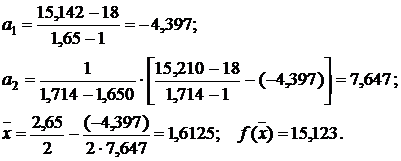
а)
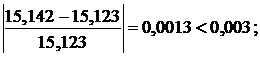 б)
б) 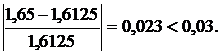
Оба критерия останова выполняются, следовательно, поиск закончен.
Ответ: x=1,6124 (точное решение x=1.5874).
