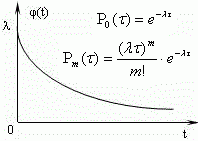Теория массового обслуживания (СМО)
Теория массового обслуживания исследует на основе теорий вероятностей математические методы количественной оценки процессов массового обслуживания. Общей особенностью всех задач, связанных с массовым обслуживанием, является случайный характер исследуемых явлений.Сервис представлен тремя онлайн-калькуляторами:
- Одноканальные СМО.
- Многоканальные СМО.
- Замкнутые системы массового обслуживания СМО.
Для решения задач на тему Теория массового обслуживания
необходимо определиться с типом модели СМО: одноканальные (см. примеры задач для одноканальных СМО) или многоканальные (см. примеры задач для многоканальных СМО). В многоканальных СМО количество устройств обслуживания n (количество рабочих, кассиров, бригад, моек и т.п.) больше одного. Обычно интенсивность потока заявок λ задана явно. Интенсивность потока обслуживания μ может задаваться в виде времени обслуживания tобс.
В сервисе необходимо ввести либо параметр μ, либо tобс (только одно из двух).
Выбор СМО зависит как от числа каналов n, так и от допустимой длины очереди m. По указанным признакам различается ряд типов СО, перечисленных в таблице.
| № п/п | Параметры СО | Тип СО | |
| n | m | ||
| 1 | 1 | 0 | Одноканальная, без очереди |
| 2 | n > 1 | 0 | Многоканальная, без очереди |
| 3 | 1 | 1 < m <∞ | Одноканальная, с ограниченной очередью |
| 4 | n > 1 | 1 < m<∞ | Многоканальная, с ограниченной очередью |
| 5 | 1 | m = ∞ | Одноканальная, с неограниченной очередью |
| 6 | n > 1 | m = ∞ | Многоканальная, с неограниченной очередью |
В зависимости от целочисленного значения m используются следующие названия в классификации типов СО:
- m = 0 – без очереди;
- m > 0 – с очередью.
Если m не ограничено, что иногда условно записывают как m = ∞ , то соответствующая СО называется системой с ожиданием. В СО данного типа пришедшая заявка при отсутствии возможности немедленного обслуживания ожидает обслуживания, какой бы длинной ни были очередь и продолжительность времени ожидания.
Все СМО делятся на СМО с отказами (параметр m не используется), СМО с ограниченной длиной очереди и СМО с неограниченной очередью. Параметр m (длина очереди) используется для последних двух СМО. При этом в СМО с неограниченной очередью можно указывать любое значение m. Например, m = 3. Тогда будут рассчитаны вероятности нахождения в очереди 1,2,3 заявки.
Временные параметры рассчитываются в часах или в минутах, в зависимости от заданного параметра λ.
Полученное решение сохраняется в файле Word. Для редактирования формул можно использовать редактор формул Microsoft Equation.
Перейти к онлайн решению своей задачи
Формулы для расчета параметров простейших СМО
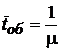 ,
, | Показатели эффективности системы | Чистая СМО с отказами (n, a) | СМО с ограничением на время пребывания в очереди (n, a,b) | СМО с ограничением на длину очереди (n, a,m) | Чистая СМО с ожиданием (n, a), γ < 1 |
| 1 | 2 | 3 | 4 | 5 |
| Вероятность того, что все каналы свободны | р0 = 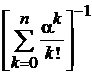
| р0= 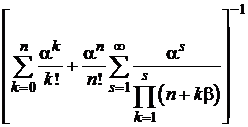
| p0=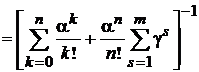
| 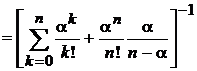
|
| Вероятность того, что занято k каналов 0 ≤ k≤ n | Рk = | Рk= | рk= | Рk = |
| Вероятность того, что заняты все n каналов, s заявок в очереди | - | рn+s = рn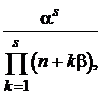 , ,
| рn+s= γs× рn; 1 ≤ s ≤ m. | рn+s=γs× рn |
| Вероятность отказа | ротк = рn | ротк = | ротк = рn+m | ротк = 0 |
| Вероятность полной загрузки системы | рn.з = рn | рn.з = 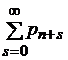
| рn.з = рn | рn.з = 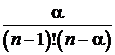
|
| Вероятность обслуживания, относительная пропускная способность системы | робс = | робс = | робс = | робс = |
| Абсолютная пропускная способность системы | lb = l·робс | lb = l·робс = l - n·r | lb = lробс = m × n3 | lb = l |
| Вероятность занятости канала | рзк = kз = | рзк = kз = | рзк = kз = | рзк = kз = |
| Среднее число свободных каналов | n0 = 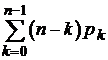
| n0 = 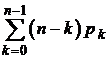
| n0 = 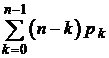
| n0 = 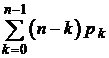
|
| Вероятность простоя канала pп.к, коэффициент простоя оборудования кn | рn.к = kn = | рn.к = kn = | рn.к = kn = | рn.к = kn = |
| 1 | 2 | 3 | 4 | 5 |
| Среднее число заявок в очереди | - | r = 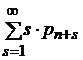
| r = 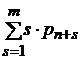
| r = рn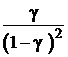
|
| Вероятность наличия очереди | - | рн.о = 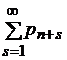
| 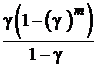
| рн.о =pn |
| Среднее время наличия очереди | - | - | 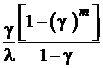
| 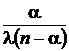
|
| Среднее время пребывания заявки в очереди | - | |||
| Среднее время пребывания заявки в системе | ||||
| Среднее время занятости канала (любого) | 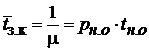
| 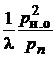
| 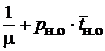
| |
| Среднее время простоя канала | 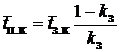
| 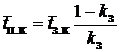
| 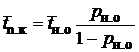
| 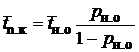
|
| Среднее время полной загрузки системы | 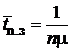
| - | 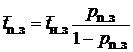
| 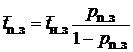
|
| Среднее время неполной загрузки системы | 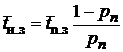
| – | 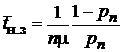
| 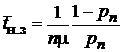
|