Онлайн-калькуляторы по линейному программированию
В этом разделе представлены онлайн-калькуляторы по линейному программированию. Линейное программирование представляет собой раздел математики, занимающийся изучением оптимальных задач, характеризующихся линейной зависимостью между переменными и разработкой методов их решения.- Графический метод решения задач линейного программирования. 1) построение области D (ОДЗ); 2) нахождение gradF и его построение; 3) нахождение экстремума функции по первой и последней точкам области D.
- Симплекс-метод - метод последовательного улучшения плана, позволяющий за конкретное число шагов получить оптимальный план решения задач по ЛП и по соответствующим оценкам функции.
- Задача о смесях
- Задача линейного программирования сводится к приведению к канонической форме, а затем к стандартной форме ЗЛП
- Двойственный симплекс-метод (P-метод)
- Составление и решение двойственной задачи
- Метод Гомори.
- Задачи параметрического программирования
- Дробно-линейное программирование
Система линейных неравенств, определяющая допустимое множество решения задачи, называется системой ограничений задачи линейного программирования, а линейная функция f(x) называется целевой функцией или критерием оптимальности. При этом запись вида f(x)→extrm означает, что необходимо найти и минимальное, и максимальное значение функции.
Как решать симплексным методом
В заданиях, требующих решения симплексным методом, присутствуют система ограничений с n неизвестными Xn и целевая функция F(x). В сервисе необходимо сначала задать количество неизвестных n и количество ограничений. Например,0.1x1+0.2x2+0.4x3≤1100
0.05x1+0.02x2+0.02x3≤120
Здесь количество неизвестных n = 3, количество строк k = 2.
Предварительно ЗЛП можно привести к канонической форме с помощью данного калькулятора, а затем к СЗЛП.
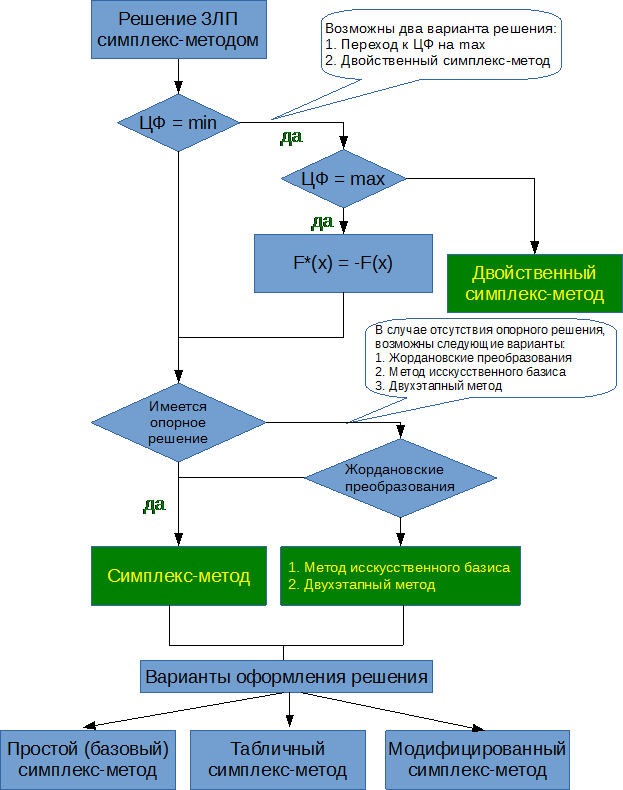
Далее необходимо выбрать форму решения симплексного метода. От этого будет зависеть не только оформление задачи, но и способ перерасчета симплекс-преобразований. Обычно в заданиях требуют решить:
- симплекс-методом. Выбирается любая форма записи.
- M-методом. Выбирается Симплекс-таблица.
- двухфазным или двухэтапным симплекс-методом. Выбираются любые из следующих форм записи: модифицированный симплексный метод, столбцовая форма, в строчечной форме или базовый симплекс-метод (по умолчанию).
- модифицированным симплекс-методом (или симплексным методом в матричной форме). Используется основной онлайн-калькулятор Симплекс-метод.
- P-методом (или двойственным симплекс-методом). Это задача на поиск минимума целевой функции F(x) = min. Решается только P-методом.
- Метод Гомори. Используется для поиска целочисленного решения.
- двойственную задачу. Для этого воспользуйтесь сервисом Двойственная задача.
Для пунктов 1,2,3,4 используется основной тип калькулятора Симплекс-метод.
Целевая функция имеет два значения: min (минимум) и max (максимум). Минимум целевой функции можно найти двумя способами:
- Свести задачу к задаче поиска максимума (для этого необходимо выбрать пункт
Задачу на min решать, перейдя к задаче на max (F(X)* = -F(X))
); - Использовать P-метод (двойственный симплексный метод).
Отметьте пункт Использовать дроби, если необходимо все вычисления записывать в виде дробей. Если исходные данные заданы с десятичной точкой, то все решение ведется без дробей.
В каждом сервисе рекомендуется сразу проверять решение в Excel (см. ссылку для скачивания шаблона после решения).
см. также Базисные решения системы линейных уравнений методом Жордана-Гаусса.
Двойственный симплекс метод в Excel.
Пошагово изучить особенности жордановских преобразований можно с помощью сервиса Правило прямоугольника.
Многокритериальная оптимизация
Список литературы
- Балдин К.В., Рукосцев А.В., Башлыков В.Н.Математические методы и модели в экономике: учебник. М.: Изд-во «Флита»; НОУ ВПО «МПСИ», 2012. 328 с. ЭБС «КнигаФонд».
- Васильев Ф.П. Методы оптимизации: В 2-х кн. — Новое изд., перераб. и доп. М.: МЦНМО, 2011. - 620 с. ЭБС «КнигаФонд».
- Гусева Е.Н. Экономико-математическое моделирование: учебное пособие. М.: Изд-во «Флинта», МПСИ, 2011. —216 с. ЭБС «КнигаФонд».
- Колемаев В.А. Математическая экономика: Учебник для вузов. М.: Изд-во: «ЮНИТИ-ДАНА», 2012. — 400 с. ЭБС «КнигаФонд».
- Спешилова Н.В., Шеврина Е.В., Корабейникова О.А. Экономико-математические модели и их практическое применение в АПК: учебное пособие. – 4-е изд., перераб. и доп. Оренбург: Издательский центр ОГАУ, 2012. 132 с.
- Федосеев В.В. Математическое моделирование в экономике и социологии труда. Методы, модели, задачи: учебное пособие. М.: Изд-во:
- Экономико-математические методы и прикладные модели: Учебное пособие/ Под ред. Федосеева В.В. М.: Изд-во «ЮНИТИ-ДАНА», 2012. 302 с. ЭБС «КнигаФонд».