Метод ветвей и границ
Назначение сервиса. Сервис предназначен для решения задач целочисленного линейного программирования в онлайн режиме методом ветвей и границ. Другое название метода - метод Ленд и Дойг. При двух переменных (x1, x2) применяется графическое решение, при большем количестве переменных - симплексный метод. В ходе решения формируется Дерево решения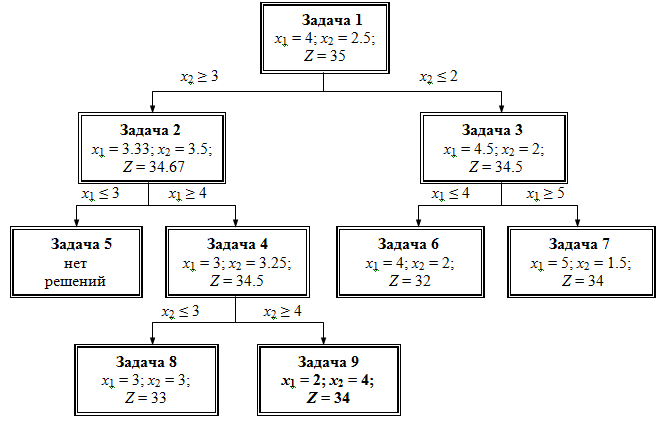 задачи.
Суть метода ветвей и границ состоит в последовательном переборе вариантов, рассмотрении лишь тех из них, которые по определенным признакам оказываются перспективными, и отбрасывании бесперспективных вариантов.
При использовании метода ветвей и границ область допустимых решений (ОДР) исходной задачи определенным способом разбивается на непересекающиеся подмножества, и решаются подзадачи, т.е. задачи на этих подмножествах с той же ЦФ и без учета условия целочисленности (как задачи ЛП). Если в результате получено оптимальное нецелочисленное решение, ОДР подзадачи снова разбивается на части и этот процесс продолжается до тех пор, пока не будет найдено оптимальное целочисленное решение исходной задачи.
Если в задаче на максимум при решении подзадач получаются оптимальные целочисленные решения, то запоминаются те из них, которым соответствуют возрастающие значения ЦФ. Если полученное «непрерывное» решение подзадачи оказывается не лучше сохраненного целочисленного решения, то такая подзадача исключается из списка задач. Название этого метода объясняется тем, что в процессе решения задача последовательно «ветвится», разбиваясь на более простые подзадачи.
Примечание: метод ветвей и границ используется также и в задаче коммивояжера.
Пример №1. В задаче методом Гомори (или методом ветвей и границ) найти оптимальные решения задач целочисленного линейного программирования. Дать геометрическую интерпретацию процесса решений задач.
Z=3x1 + 2x2 → max
при ограничениях:
x1 + x2 ≤ 13
x1 - x2 ≤ 6
-3x1 + x2 ≤ 9
x1≥0, x2 ≥0
x1, x2 – целые числа.
Пример №2.
5x1 + 2x2 ≤ 14
2x1 + 5x2 ≤ 16
x1 , x2 – целые числа
Z = 3x1 + 5x2 → max
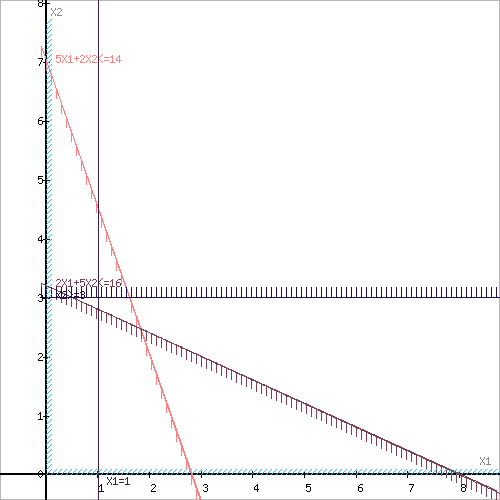
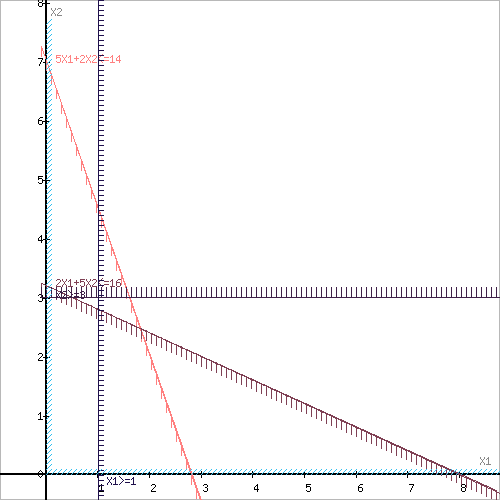
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
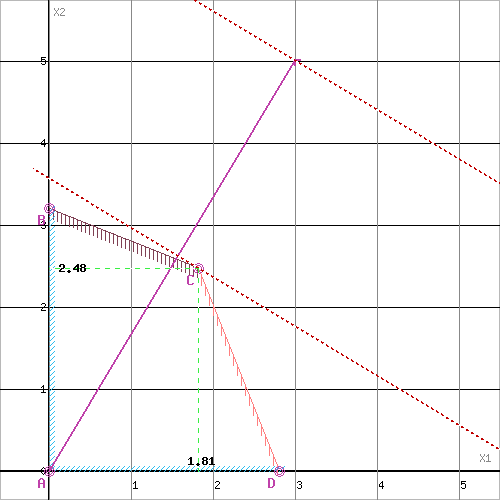
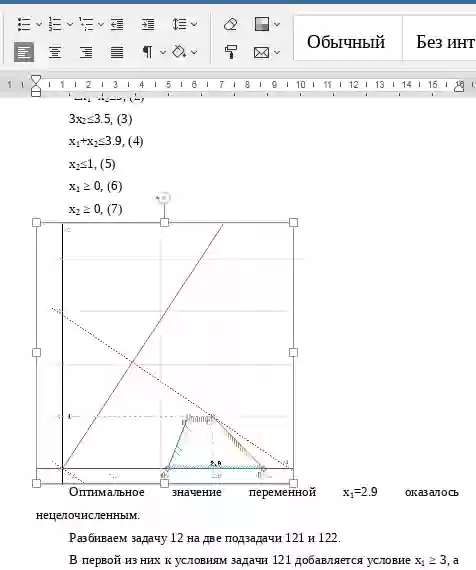
Оптимальное значение переменной x1=1.81 оказалось нецелочисленным.
Разбиваем задачу 1 на две подзадачи 11 и 12.
В первой из них к условиям задачи 11 добавляется условие х1 ≥ 2, а к задаче 12 — условие х1 ≤ 1.
Эта процедура называется ветвлением по переменной х1.
Решим графически задачу 11 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x1≥2 (3)
x1≥0 (4)
x2≥0 (5)
Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
5x1+2x2≤14
x1≥2
Решив систему уравнений, получим: x1 = 2, x2 = 2
Откуда найдем максимальное значение целевой функции:
F(X) = 3*2 + 5*2 = 16
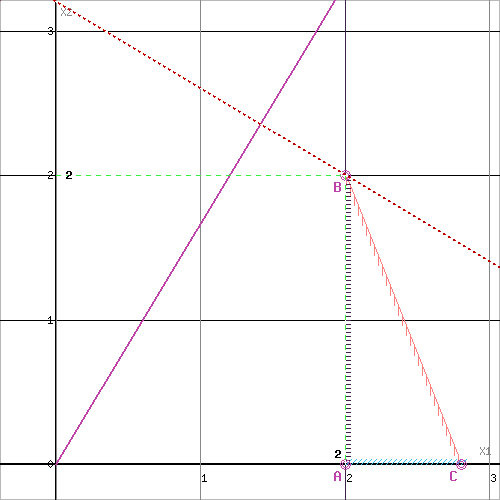
Решение задачи получилось целочисленным.
Новое значение текущего рекорда будет равно F(X) = 16.
Так как найденная точка является первым целочисленным решением, то ее и соответствующее ей значение ЦФ следует запомнить. Сама точка называется текущим целочисленным рекордом или просто рекордом, а оптимальное значение целочисленной задачи — текущим значением рекорда. Это значение является нижней границей оптимального значения исходной задачи Z*.
Решим графически задачу 12 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x1≤1 (3)
x1≥0 (4)
x2≥0 (5)
Область допустимых решений представляет собой многоугольник
Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
2x1+5x2≤16
x1≤1
Решив систему уравнений, получим: x1 = 1, x2 = 2.8
Откуда найдем максимальное значение целевой функции:
F(X) = 3*1 + 5*2.8 = 17
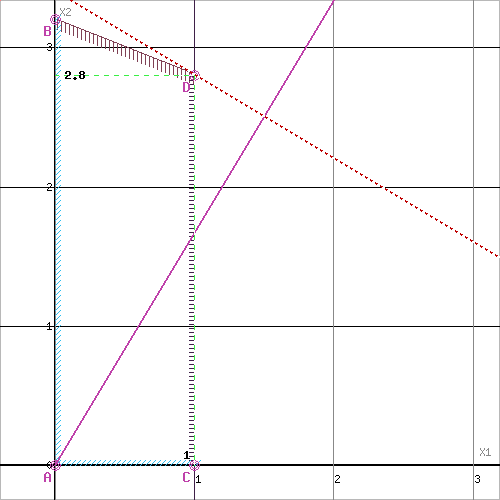
Оптимальное значение переменной x2=2.8 оказалось нецелочисленным.
Разбиваем задачу 12 на две подзадачи 121 и 122.
В первой из них к условиям задачи 121 добавляется условие х2 ≥ 3, а к задаче 122 — условие х2 ≤ 2.
Решим графически задачу 121 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x1≤1 (3)
x2≥3 (4)
x1≥0 (5)
x2≥0 (6)
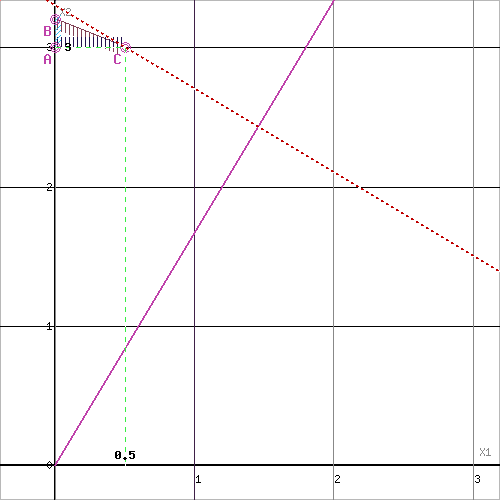
Решим графически задачу 122 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x1≤1 (3)
x2≤2 (4)
x1≥0 (5)
x2≥0 (6)
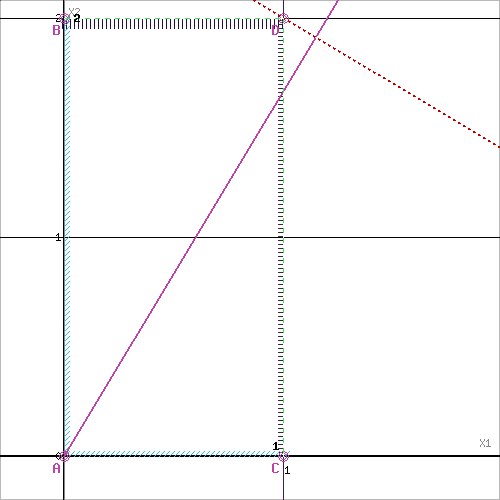
Текущий рекорд Z=16≥13, поэтому прекращаем ветвление из этой вершины
Оптимальное значение переменной x1=0.5 оказалось нецелочисленным.
Разбиваем задачу 121 на две подзадачи 1211 и 1212.
В первой из них к условиям задачи 1211 добавляется условие х1 ≥ 1, а к задаче 1212 — условие х1 = 0.
Решим графически задачу 1211 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x1≤1 (3)
x2≥3 (4)
x1≥1 (5)
x1≥0 (6)
x2≥0 (7)
Сведем систему ограничений к следующему виду:
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x1=1 (3)
x2≥3 (4)
x1≥0 (5)
x2≥0 (6)
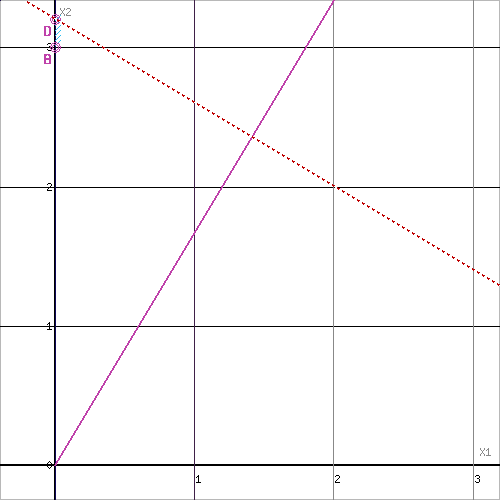
Задача не имеет допустимых решений. ОДР представляет собой пустое множество.
Задача 1211 не имеет решения, поэтому для нее процесс ветвления прерываем.
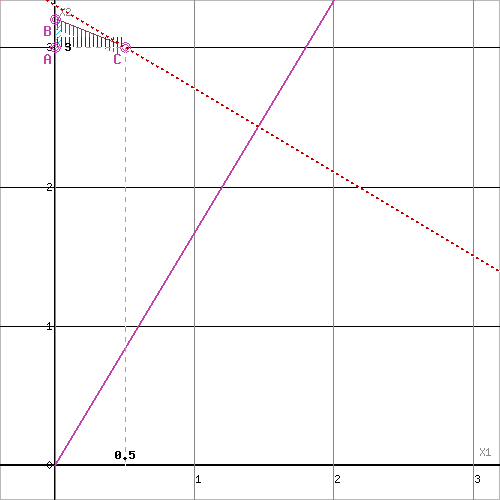
Решим графически задачу 1212 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x1≤1 (3)
x2≥3 (4)
x1=0 (5)
x1≥0 (6)
x2≥0 (7)
Текущий рекорд Z=16≥16, поэтому прекращаем ветвление из этой вершины
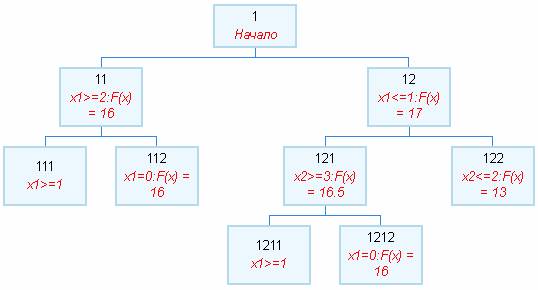
Оптимальное значение переменной x2=2.48 оказалось нецелочисленным. Разбиваем задачу 1 на две подзадачи 11 и 12.
В первой из них к условиям задачи 11 добавляется условие х2 ≥ 3, а к задаче 12 — условие х2 ≤ 2.
Эта процедура называется ветвлением по переменной х2.
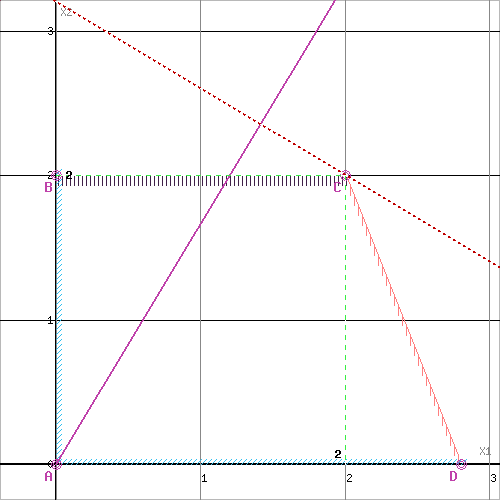
Решим графически задачу 11 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x2≥3 (3)
x1≥0 (4)
x2≥0 (5)
Решим графически задачу 12 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x2≤2 (3)
x1≥0 (4)
x2≥0 (5)
Текущий рекорд Z=16≥16, поэтому прекращаем ветвление из этой вершины
Оптимальное значение переменной x1=0.5 оказалось нецелочисленным. Разбиваем задачу 11 на две подзадачи 111 и 112. В первой из них к условиям задачи 111 добавляется условие х1 ≥ 1, а к задаче 112 — условие х1 = 0.
Решим графически задачу 111 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x2≥3 (3)
x1≥1 (4)
x1≥0 (5)
x2≥0 (6)
Задача не имеет допустимых решений. ОДР представляет собой пустое множество
Задача 111 не имеет решения, поэтому для нее процесс ветвления прерываем.
Решим графически задачу 112 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x2≥3 (3)
x1=0 (4)
x1≥0 (5)
x2≥0 (6)
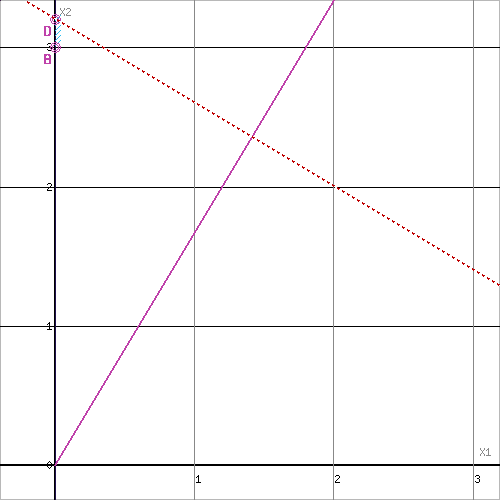
Текущий рекорд Z=16≥16, поэтому прекращаем ветвление из этой вершины
F(X) = 16
x1 = 2
x2 = 2
Дерево решения задачи
