Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
Правила ввода функции, заданной в явном виде
Можно указывать без левой части, например, просто cos(x)^2-sin(x), либо с левой частью: f(x)=cos(x)^2-sin(x). Если дифференцирование происходит не по переменной x, то левую часть необходимо указать, например: f(z)=cos(z)^2-a*sin(z).Правила ввода функции, заданной в неявном виде
Если функция задана в видеy2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y), либо f(x;y)=y^2-x-cos(y).
Примеры
Правила ввода функции, заданной в параметрическом виде
Функции отделяются через знак;, например, x=cos(t);y=sin(t)
Примеры
Вместе с этим калькулятором также используют следующие:
Таблица производных
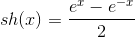 – гиперболический синус
– гиперболический синус
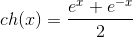 – гиперболический косинус
– гиперболический косинус
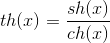 – гиперболический тангенс
– гиперболический тангенс
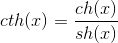 – гиперболический котангенс
– гиперболический котангенс
- (xα)’ = α xα-1
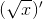 = 1/2x1/2 =
= 1/2x1/2 = 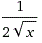
- (ax)’ = ax·lna
- (ex)’ = ex
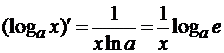
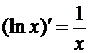
- (sinx)’ = cosx
- (cosx)’ = -sinx
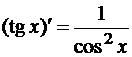
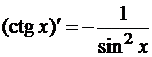
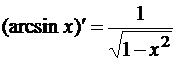
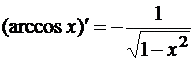
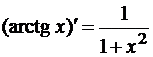
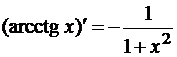
- (shx)’ = chx
- (chx)’ = shx
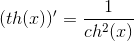
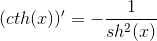
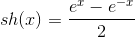 – гиперболический синус
– гиперболический синус
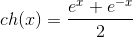 – гиперболический косинус
– гиперболический косинус
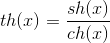 – гиперболический тангенс
– гиперболический тангенс
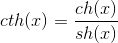 – гиперболический котангенс
– гиперболический котангенс
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функцииy=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
![]() .
.
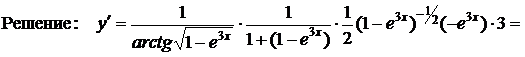
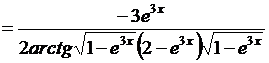 .
.
В некоторых случаях, если, например, нужно найти производную функции
y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции
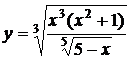 .
.
Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию
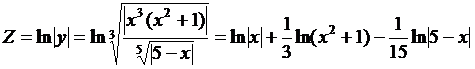
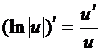 , будем иметь
, будем иметь
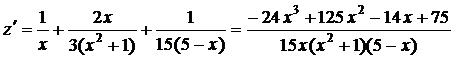
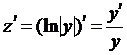 , откуда
, откуда
 .
.
Пример 4. Найти производную функции y=xex
Решение.
![]()
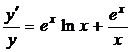 ;
;
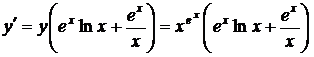 .
.
Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
