Вычисление интегралов
Множество всех первообразных функции f(x) (дифференциала f(x)dx) называется неопределенным интегралом от этой функции и обозначается ∫f(x)dx.x3sin(x2). Запишем как x^3*sin(x^2) и нажимаем кнопку Получить решение.
Если интеграл определенный, например,
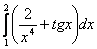, то записываем 2/x^4+tan(x), в качестве пределов интегрирования указываем 1, 2. Первая строка служит для ввода числителя функции, вторая - для знаменателя.
Примечание: число "пи" (π) записывается как pi; знак "бесконечность" (∞) ≡ infinity
Примеры правильной записи некоторых выражений
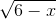 | sqrt(6-x) |
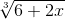 | (6+2*x)^(1/3) |
| log5(1+x) | log(1+x,5) |
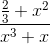 | (2/3+x^2)/(x^3+x) |
Точки разрыва функции
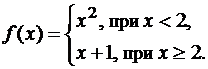
Производная функции:
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление пределов
Приемы нахождения неопределенных интегралов
Способы нахождения неопределенных интегралов:- Подведение под знак дифференциала:
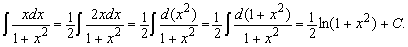
- Интегрирование по частям: ∫xexdx
- Простейшие преобразования подынтегрального выражения (пример):
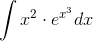
- Интегрирование рациональных дробей:
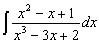
- Интегрирование простейших иррациональностей:
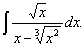
- Интегрирование выражений, содержащих тригонометрические функции: ∫cos4(x)sin3(x)dx
см. также Задача интегрирования в конечном виде, Несобственные интегралы
Пример 1. Вычислить ∫(3x+15)17dx.
Решение.
Возводить двучлен в 17-ю степень нецелесообразно. Исходя из табличного интеграла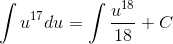 
, получаем
= 
.
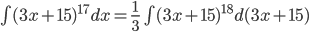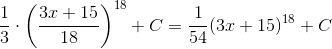Пример 2. Вычислить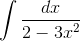 
.
Решение.
Аналогично предыдущему,
= 
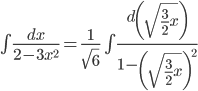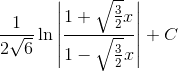
Пример 3.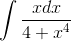 
.
Решение. Поскольку
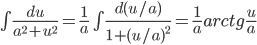, то 
.
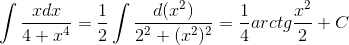Пример 4. Вычислить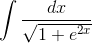 
Решение. Так как
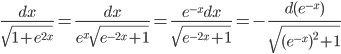, то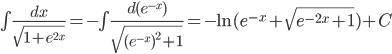 
.
Пример 5. Вычислить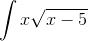 
.
Решение.
Применим подстановку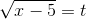 
. Отсюда x-5=t2, x=t2+5, dx=2tdt.
Подставив в интеграл, получим
= 
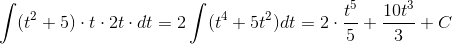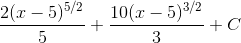
Пример 6. Вычислить ∫x2exdx.
Решение.
Положим u=x2, dv=exdx; тогда du=2xdx, v=ex. Применим формулу интегрирования по частям:
∫x2exdx=x2ex-2∫xex.
Мы добились понижения степени x на единицу. Чтобы найти ∫xex, применим еще раз интегрирование по частям. Полагаем u=x, dv=exdx; тогда du=dx, v=ex и
∫xex=x2ex-2xex+2ex+C.
Пример 7. Вычислить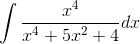 
.
Решение. Выделяя целую часть, получим: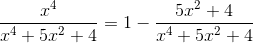 
.
Учитывая, что x4+5x2+4=(x2+1)(x2+4), для второго слагаемого получаем разложение
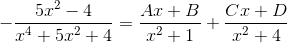
Приводя к общему знаменателю, получим равенство числителей:
-5x2–4=(Ax+B)(x2+4)+(Cx+D)(x2+1).
Приравнивая коэффициенты при одинаковых степенях x, получаем
x3: 0=A+C
x2: -5=B+D
x: 0=4A+C
x0: -4=4B+D
Отсюда находим A=C=0, B=1/3, D=-16/3.
Подставляя найденные коэффициенты в разложение и интегрируя его, получаем:
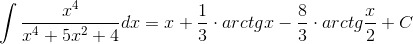
Пример 8. Вычислить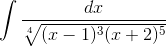 
.
Решение. Так как
,
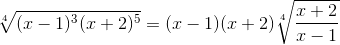то подынтегральное выражение есть рациональная функция от x и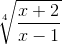 
; поэтому введем подстановку:
; 
,
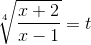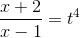откуда
; 
; 
;
.
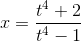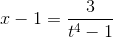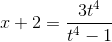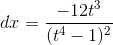Следовательно,
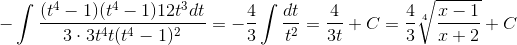
Пример 9. Вычислить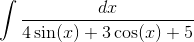 
.
Решение.
Подынтегральная функция рационально зависит от sinx(x) и cos(x); применим подстановку tgx/2=t, тогда
, 
, 
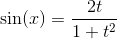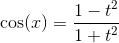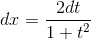и
= 
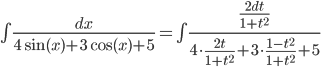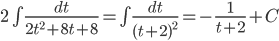
Возвращаясь к старой переменной, получим
= 
.
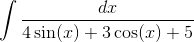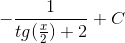Пример 10. Вычислить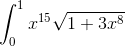 
.
Решение.
Произведем замену 1+3x8 = z2. Тогда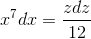 
, 
;
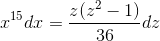таким образом,
.
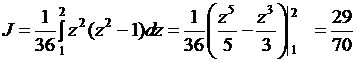Следует обратить внимание, что при замене переменной в определенном интеграле пределы интегрирования в общем случае изменяются.
Пример 11.Вычислить несобственный интеграл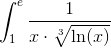 
или доказать его расходимость.
Решение. Подынтегральная функция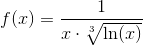 
не ограничена в окрестности точки x=1. На любом же отрезке [1+ε;e] она интегрируема, так как является непрерывной функцией. Поэтому
.
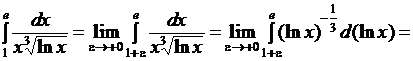
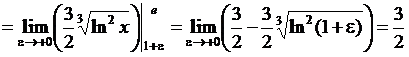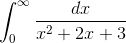или доказать его расходимость.
Решение.
Подынтегральная функция непрерывна и интегрируема на R. По определению
= 
= 
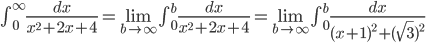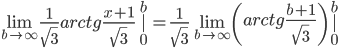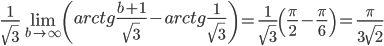
Пример 13. Найти площадь фигуры, ограниченной параболой y=x2 и прямой x+y=2.
Решение.
Найдем абсциссы точек пересечения параболы y=x2 и прямой y=2-x. Решая уравнение x2=2-x, находим x1=-2, x2=1. Так как фигура ограничена сверху прямой, а снизу параболой, по известной формуле находим
.
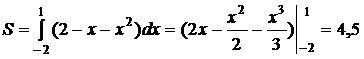