Дифференциал функции

Полный дифференциал для функции двух переменных: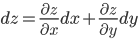

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz

• Ввод данных
• Инструкция
• Оформление Word
• Также решают

f(x) =

...load... Действия

• Загрузить предыдущие

Видеоинструкция

Примеры
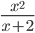≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
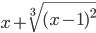≡ x+(x-1)^(2/3)

Скачать пример оформления

Вместе с этим калькулятором также используют следующие:
Точки разрыва функции


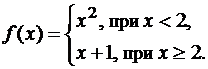
Решение пределов
Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных
Вычисление интегралов

см. также Вычисление приближенно с помощью дифференциала

Определение. Функция y=f(x) называется дифференцируемой в точке x₀, если ее приращение в этой точке можно представить в виде ∆y=A∆x + α(∆x)∆x, где A – константа, а α(∆x) – бесконечно малая при ∆x → 0.
Требование дифференцируемости функции в точке эквивалентно существованию производной в этой точке, причем A=f’(x₀).

Пусть f(x) дифференцируема в точке x₀ и f '(x₀)≠0, тогда ∆y=f’(x₀)∆x + α∆x, где α= α(∆x) →0 при ∆x→0. Величина ∆y и каждое слагаемое правой части являются бесконечно малыми величинами при ∆x→0. Сравним их: 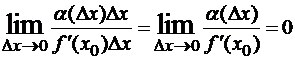, то есть α(∆x)∆x – бесконечно малая более высокого порядка, чем f’(x₀)∆x.

то есть ∆y~f’(x₀)∆x. Следовательно, f’(x₀)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x₀ и обозначают dy(x₀) или df(x₀). Итак, для произвольных значений x
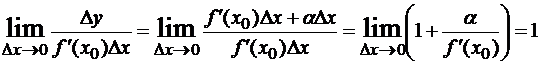
dy=f′(x)∆x. (1)
Полагают dx=∆x, тогда
dy=f′(x)dx. (2)

Пример. Найти производные и дифференциалы данных функций.
а) y=4tg2x
Решение:

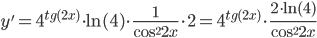
дифференциал: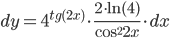
б)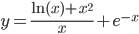
Решение:

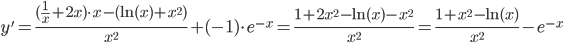
дифференциал: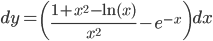
в) y=arcsin2(lnx)
Решение:

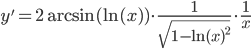
дифференциал: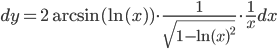
г)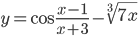
Решение:
=
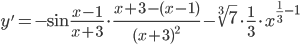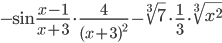
дифференциал: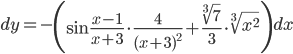

Пример. Для функции y=x³ найти выражение для ∆y и dy при некоторых значениях x и ∆x.
Решение. ∆y = (x+∆x)³ – x³ = x³ + 3x²∆x +3x∆x² + ∆x³ – x³ = 3x²∆x+3x∆x²+∆x³; dy=3x²∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x² + ∆x³.