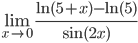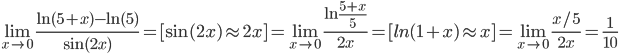Решение пределов
Число A называется пределом функцииy=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
Например, найти предел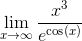 
запишем как x^3/exp(cos(x)). В качестве предела указываем (нажимаем) .
Для наглядности можно отдельно заполнить числитель x^3 и знаменатель функции exp(cos(x)). Примечание: число "пи" (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
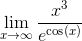запишем как x^3/exp(cos(x)). В качестве предела указываем (нажимаем) .
Для наглядности можно отдельно заполнить числитель x^3 и знаменатель функции exp(cos(x)). Примечание: число "пи" (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
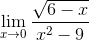 | sqrt(6-x)/(x^2-9) |
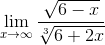 | sqrt(6-x)/(6+2*x)^(1/3) |
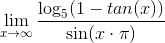 | log(1-tan(x),5)/sin(x*pi) |
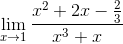 | (x^2+2*x-2/3)/(x^3+x) |
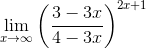 | ((3-3*x)/(4-3*x))^(2*x+1) |
Вместе с этим калькулятором также используют следующие:
Точки разрыва функции
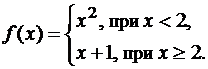
Производная функции:
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление интегралов
Точки разрыва функции
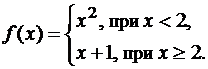
Производная функции:
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление интегралов
Примеры.
Вычислить указанные пределы:
1. 
= 
.
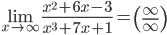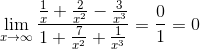2. 
= 
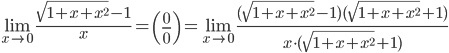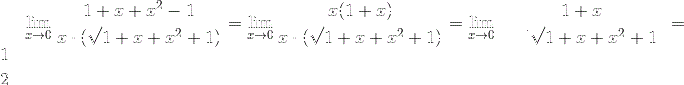
3. = 
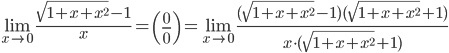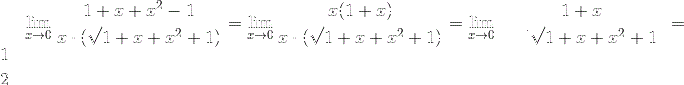
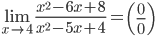. Так как числитель и знаменатель обратились в нуль при x=4, то 4 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-4). Получаем
.
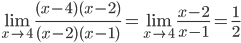4. 
.
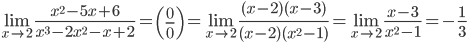5.
= 
= 
.
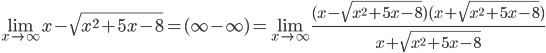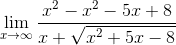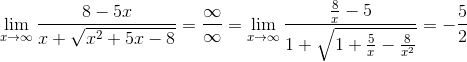
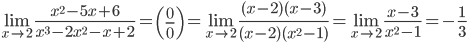5.
= =
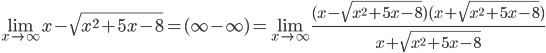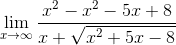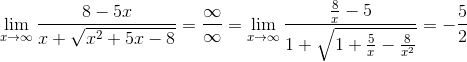
6. 
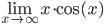– не существует, так как -1<cos(x)<1.
7. 
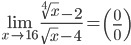. Обозначим 
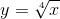, причем заметим, что при x→16, y→2. Получим:
.
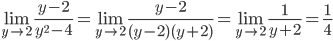8. 
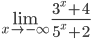. (Ответ получается непосредственно подстановкой (-∞) вместо x.)
9. 
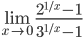. Здесь следует рассмотреть односторонние пределы:
; 
.
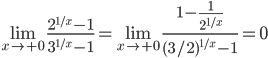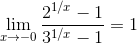Следовательно,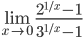 
– не существует (так как у функции разные односторонние пределы).
Найти пределы функции, не применяя правило Лопиталя.
а)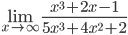
= 
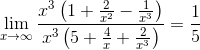
Ответ: 1/5
б)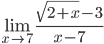 
= 
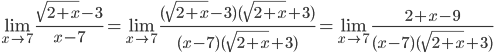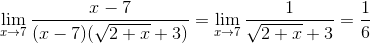
в)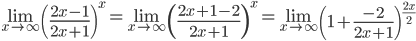 
=
Ответ: 1/e
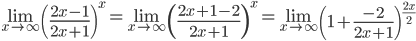= e-2/2 = e-1г)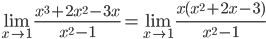 
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-1).
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
, 
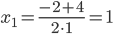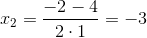
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
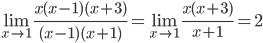
Ответ: 2
д) 
