Интегрирование по частям
Пусть U(x) и V(x) - дифференцируемые функции. Тогдаd(U(x)V(x)) = U(x)dV(x) + V(x)dU(x). Поэтому U(x)dV(x) = d(U(x)V(x)) – V(x)dU(x). Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫d(U(x)V(x))=U(x)V(x)+C, получаем соотношение
С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word.
Также рекомендуется изучить сервис вычисление интегралов онлайн
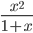≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
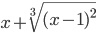≡ x+(x-1)^(2/3)
Применение метода интегрирования по частям
В связи с особенностями нахождения определенных величин, формулу интегрирования по частям очень часто используют в следующих задачах:- Математическое ожидание непрерывной случайной величины. Формула для нахождения математического ожидания и дисперсии непрерывной случайной величины включает в себя два сомножителя: функцию полинома от x и плотность распределения f(x).
- Разложение в ряд Фурье. При разложении необходимо определять коэффициенты, которые находятся интегрированием от произведения функции f(x) и тригонометрической функции cos(x) или sin(x).
Типовые разложения по частям
| Вид интеграла | Разложения на части |
∫Pn(x)cos(ax)dx, ∫Pn(x)sin(ax)dx, ∫Pn(x)eaxdx, где Pn(x) - некоторый полином (многочлен) степени n | U(x)=Pn(x), dV(x)=cos(ax)dx |
∫ln(P(x))dx | U=ln(P(x)); dV=dx |
∫arcsin(ax)dx | U=arcsin(ax); dV=dx |
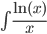 | U=ln(x); dV=dx/x |
При использовании формулы интегрирования по частям нужно удачно выбрать U и dV, чтобы интеграл, полученный в правой части формулы находился легче. Положим в первом примере U=ex, dV=xdx. Тогда dU=exdx,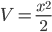 
и 
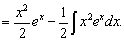Вряд ли интеграл
Иногда требуется применить формулу интегрирования по частям несколько раз, например, при вычислении интеграла
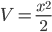и Вряд ли интеграл ∫x2exdx можно считать проще исходного.
Иногда требуется применить формулу интегрирования по частям несколько раз, например, при вычислении интеграла
∫x2sin(x)dx.
Интегралы ∫eaxcos(bx)dx и ∫eaxsin(bx)dx называются циклическими и вычисляются с использованием формулы интегрирования по частям два раза.
Пример №1. Вычислить ∫xexdx.
Положим U=x, dV=exdx. Тогда dU=dx, V=ex. Поэтому ∫xexdx=xex-∫exdx=xex-ex+C.
Пример №2. Вычислить ∫xcos(x)dx.
Полагаем U=x, dV=cos(x)dx. Тогда dU=dx, V=sin(x) и ∫xcos(x)dx=xsin(x) - ∫sin(x)dx = xsin(x)+cos(x)+C
Пример №3. ∫(3x+4)cos(x)dx
Решение:
(3x+4)sin(x)+3cos(x)+C
