Решение транспортной задачи
Инструкция. Для получения решения транспортной задачи в онлайн режиме выберите размерность матрицы тарифов (количество поставщиков и количество магазинов).Графический метод решения ЗЛП
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Задачи динамического программирования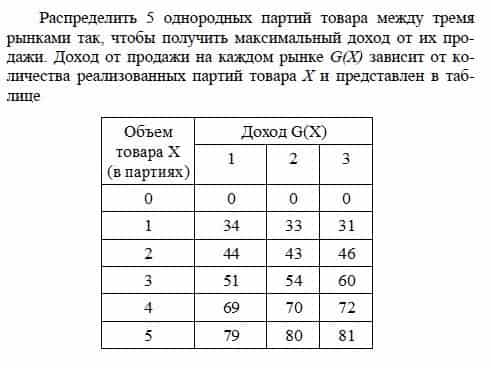
Первым этапом решения транспортной задачи является определение ее типа (открытая или закрытая, или иначе сбалансированная или не сбалансированная). Приближенные методы (методы нахождения опорного плана) позволяют на втором этапе решения за небольшое число шагов получить допустимое, но не всегда оптимальное, решение задачи. К данной группе методов относятся методы:
- вычеркивания (метод двойного предпочтения);
- северо-западного угла;
- минимального элемента;
- аппроксимации Фогеля.
Опорное решение транспортной задачи
Опорным решением транспортной задачи называется любое допустимое решение, для которого векторы условий, соответствующие положительным координатам, линейно независимы. Для проверки линейной независимости векторов условий, соответствующих координатам допустимого решения, используют циклы.Циклом называется такая последовательность клеток таблицы транспортной задачи, в которой две и только соседние клетки расположены в одной строке или столбце, причем первая и последняя также находятся в одной строке или столбце. Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,...,m; j=1,2,...,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла.
Приближенные методы решения транспортной задачи.
Метод вычеркивания (метод двойного предпочтения). Если в строке или столбце таблицы одна занятая клетка, то она не может входить в какой-либо цикл, так как цикл имеет две и только две клетки в каждом столбце. Следовательно, можно вычеркнуть все строки таблицы, содержащие по одной занятой клетке, затем вычеркнуть все столбцы, содержащие по одной занятой клетке, далее вернуться к строкам и продолжить вычеркивание строк и столбцов. Если в результате вычеркивания все строки и столбцы будут вычеркнуты, значит, из занятых клеток таблицы нельзя выделить часть, образующую цикл, и система соответствующих векторов условий является линейно независимой, а решение опорным. Если же после вычеркиваний останется часть клеток, то эти клетки образуют цикл, система соответствующих векторов условий линейно зависима, а решение не является опорным.
Метод «северо-западного угла» состоит в последовательном переборе строк и столбцов транспортной таблицы, начиная с левого столбца и верхней строки, и выписывании максимально возможных отгрузок в соответствующие ячейки таблицы так, чтобы не были превышены заявленные в задаче возможности поставщика или потребности потребителя. На цены доставки в этом методе не обращают внимание, поскольку предполагается дальнейшая оптимизация отгрузок.
Метод «минимального элемента». Отличаясь простотой данный метод все же эффективнее чем, к примеру, метод Северо-западного угла. Кроме того, метод минимального элемента понятен и логичен. Его суть в том, что в транспортной таблице сначала заполняются ячейки с наименьшими тарифами, а потом уже ячейки с большими тарифами. То есть мы выбираем перевозки с минимальной стоимостью доставки груза. Это очевидный и логичный ход. Правда он не всегда приводит к оптимальному плану.
Метод «аппроксимации Фогеля». При методе аппроксимации Фогеля на каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают минимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации.
Пример №1. Матрица тарифов (здесь количество поставщиков равно 4, количество магазинов равно 6):
| 1 | 2 | 3 | 4 | 5 | 6 | Запасы | |
| 1 | 3 | 20 | 8 | 13 | 4 | 100 | 80 |
| 2 | 4 | 4 | 18 | 14 | 3 | 0 | 60 |
| 3 | 10 | 4 | 18 | 8 | 6 | 0 | 30 |
| 4 | 7 | 19 | 17 | 10 | 1 | 100 | 60 |
| Потребности | 10 | 30 | 40 | 50 | 70 | 30 |
∑a = 80 + 60 + 30 + 60 = 230
∑b = 10 + 30 + 40 + 50 + 70 + 30 = 230
Условие баланса соблюдается. Запасы равны потребностям. Итак, модель транспортной задачи является закрытой. Если бы модель получилась открытой, то потребовалось бы вводить дополнительных поставщиков или потребителей.
На втором этапе осуществляется поиск опорного плана методами, приведенными выше (наиболее распространенным является метод наименьшей стоимости).
Для демонстрации алгоритма приведем лишь несколько итераций.
Итерация №1. Минимальный элемент матрицы равен нулю. Для этого элемента запасы равны 60, потребности 30. Выбираем из них минимальное число 30 и вычитаем его (см. в таблице). При этом из таблицы вычеркиваем шестой столбец (потребности у него равны 0).
| 3 | 20 | 8 | 13 | 4 | x | 80 |
| 4 | 4 | 18 | 14 | 3 | 0 | 60 - 30 = 30 |
| 10 | 4 | 18 | 8 | 6 | x | 30 |
| 7 | 19 | 17 | 0 | 1 | x | 60 |
| 10 | 30 | 40 | 50 | 70 | 30 - 30 = 0 | 0 |
Итерация №2. Снова ищем минимум (0). Из пары (60;50) выбираем минимальное число 50. Вычеркиваем пятый столбец.
| 3 | 20 | 8 | x | 4 | x | 80 |
| 4 | 4 | 18 | x | 3 | 0 | 30 |
| 10 | 4 | 18 | x | 6 | x | 30 |
| 7 | 19 | 17 | 0 | 1 | x | 60 - 50 = 10 |
| 10 | 30 | 40 | 50 - 50 = 0 | 70 | 0 | 0 |
Итерация №3. Процесс продолжаем до тех пор, пока не выберем все потребности и запасы.
Итерация №N. Искомый элемент равен 8. Для этого элемента запасы равны потребностям (40).
| 3 | x | 8 | x | 4 | x | 40 - 40 = 0 |
| x | x | x | x | 3 | 0 | 0 |
| x | 4 | x | x | x | x | 0 |
| x | x | x | 0 | 1 | x | 0 |
| 0 | 0 | 40 - 40 = 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | Запасы | |
| 1 | 3[10] | 20 | 8[40] | 13 | 4[30] | 100 | 80 |
| 2 | 4 | 4 | 18 | 14 | 3[30] | 0[30] | 60 |
| 3 | 10 | 4[30] | 18 | 8 | 6 | 0 | 30 |
| 4 | 7 | 19 | 17 | 0[50] | 1[10] | 100 | 60 |
| Потребности | 10 | 30 | 40 | 50 | 70 | 30 |
Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 9. Следовательно, опорный план является вырожденным. Строим новый план. Иногда приходится строить несколько опорных планов, прежде чем найти не вырожденный.
| 1 | 2 | 3 | 4 | 5 | 6 | Запасы | |
| 1 | 3[10] | 20 | 8[40] | 13[30] | 4 | 100 | 80 |
| 2 | 4 | 4[20] | 18 | 14 | 3[10] | 0[30] | 60 |
| 3 | 10 | 4[10] | 18 | 8[20] | 6 | 0 | 30 |
| 4 | 7 | 19 | 17 | 0 | 1[60] | 100 | 60 |
| Потребности | 10 | 30 | 40 | 50 | 70 | 30 |
В результате получен первый опорный план, который является допустимым, так как число занятых клеток таблицы равно 9 и соответствует формуле m + n - 1 = 6 + 4 - 1 = 9, т.е. опорный план является невырожденным.
Третий этап заключается в улучшении найденного опорного плана. Здесь используют метод потенциалов или распределительный метод. На этом этапе правильность решения можно контролировать через функцию стоимости F(x). Если она уменьшается (при условии минимизации затрат), то ход решения верный.
Пример №2. Используя метод минимального тарифа, представить первоначальный план для решения транспортной задачи. Проверить на оптимальность, используя метод потенциалов.
| 30 | 50 | 70 | 10 | 30 | 10 | |
| 40 | 2 | 4 | 6 | 1 | 1 | 2 |
| 80 | 3 | 4 | 5 | 9 | 9 | 6 |
| 60 | 4 | 3 | 2 | 7 | 8 | 7 |
| 20 | 5 | 1 | 3 | 5 | 7 | 9 |
Пример №3. Четыре кондитерские фабрики могут производить три вида кондитерских изделий. Затраты на производство одного центнера (ц) кондитерских изделий каждой фабрикой, производственные мощности фабрик (ц в месяц) и суточные потребности в кондитерских изделиях (ц в месяц) указаны в таблице. Составить план производства кондитерских изделий, минимизирующий суммарные затраты на производство.
| Кондитерская фабрика | Стоимость производства одного центнера кондитерских изделий | Месячная производительность кондитерских изделий | ||
| 1 | 2 | 3 | ||
| 1 | 3 | 4 | 3 | 30 |
| 2 | 2 | 3 | 5 | 20 |
| 3 | 1 | 2 | 3 | 10 |
| 4 | 4 | 5 | 8 | 30 |
| Месячная потребность в кондитерских изделиях | 30 | 20 | 30 | |
Примечание. Здесь предварительно можно транспонировать таблицу затрат, поскольку для классической постановки транспортной задачи сначала следуют мощности (производство), а потом потребители.
| Кондитерская фабрика | Стоимость производства одного центнера кондитерских изделий | Месячная потребность в кондитерских изделиях | |||
| 1 | 2 | 3 | 4 | ||
| 1 | 3 | 2 | 1 | 4 | 30 |
| 2 | 4 | 3 | 2 | 5 | 20 |
| 3 | 3 | 5 | 3 | 8 | 30 |
| Месячная производительность кондитерских изделий | 30 | 20 | 10 | 30 | |
Пример №4. На строительство объектов кирпич поступает с трех (I, II, III) заводов. Заводы имеют на складах соответственно 50, 100 и 50 тыс. шт. кирпича. Объекты требуют соответственно 50, 70, 40 и 40 тыс. шт. кирпича. Тарифы (ден. ед./тыс.шт.) приведены в таблице. Составьте план перевозок, минимизирующий суммарные транспортные расходы.
| Завод | Тариф, ден. ед./тыс.шт. | Запасы | |||
| 1 | 2 | 3 | 4 | ||
| I | 2 | 6 | 2 | 3 | 50 |
| II | 5 | 2 | 1 | 7 | 100 |
| III | 4 | 5 | 7 | 8 | 50 |
| Потребности | 50 | 70 | 40 | 40 | |
Пример №5. Транспортная задача, заданная таблицей
| 60 | a | |
| 35 | 3 | 8 |
| 20 | 4 | 1 |
| b | 2 | 3 |
А) a=40, b=45
Б) a=45, b=40
В) a=11, b=12
Условие закрытой транспортной задачи: ∑a = ∑b
Находим, ∑a = 35+20+b = 55+b; ∑b = 60+a
Получаем: 55+b = 60+a
Равенство будет соблюдаться только при a=40, b=45



