Транспортная задача линейного программирования
Под названием «транспортная задача» объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.Формулировка транспортной задачи
Однородный груз сосредоточен у k поставщиков в объемах a 1 , а2,..., аk. Данный груз необходимо доставить и потребителям в объемах b1, b2, ..., bn. Известны сiji= 1, 2, ..., k и j = 1, 2, ..., n — стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков будут вывезены полностью, запросы всех потребителей полностью удовлетворены и суммарные затраты на перевозку всех грузов минимальны.Исходные данные транспортной задачи обычно записываются в таблицу:
| | b1 | b2 | … | bn |
|
a1 | с11 |
с12 | |
с1n |
| a2 | с21 | … | | с2n |
|
… | … |
… | … |
… |
| ak | сk1 | … | … | сkn |
Исходные данные задачи могут быть представлены также в виде вектора запасов поставщиков А = (a1, а2,..., аk), вектора запросов потребителей В= (b1, b2, ..., bn) и матрицы стоимостей C={сij}
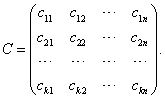
В транспортных задачах под поставщиками и потребителями понимаются различные промышленные и сельскохозяйственные предприятия, заводы, фабрики, склады, магазины и т.д. Однородными считаются грузы, которые могут быть перевезены одним видом транспорта. Под стоимостью перевозок понимаются тарифы, расстояния, время, расход топлива и т.п.
Математическая модель транспортной задачи
Переменными (неизвестными) транспортной задачи являются xij ..,i-(=1,2, ..., k), j= 1,2, ...,n — объемы перевозок от каждого i -го поставщика каждому j-му потребителю. Эти переменные можно записать в виде матрицы перевозок: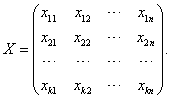
или
| | a1 | a2 | … | an |
|
b1 | x11 |
x12 | |
x1n |
| b2 | x21 | … | | x2n |
|
… | … |
… | … |
… |
| bk | xk1 | … | … | xkn |
Так как произведение cijxij . определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны
. По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция задачи имеет вид:
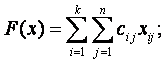
Система ограничений задачи состоит из двух групп уравнений. Первая группа из k уравнений описывает тот факт, что запасы всех k поставщиков вывозятся полностью:
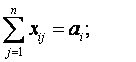
Вторая группа из n уравнений выражает требование полностью удовлетворить запросы всех n потребителей:
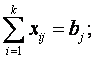
Учитывая условие неотрицательности объемов перевозок, математическую модель задачи можно записать так:
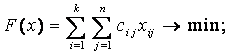
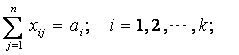
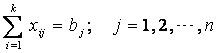
xij=≥0, i=1,2,...,k; j=1,2,...,n
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.
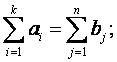
Такая задача называется задачей с правильным балансом, а ее модель — закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а ее модель — открытой.
Математическая формулировка транспортной задачи такова: найти переменные X =(xij ) задачи удовлетворяющие системе ограничений:
условиям неотрицательности
и обеспечивающие минимум целевой функции.
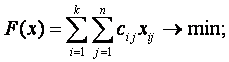
Математическая модель транспортной задачи может быть записана в векторном виде. Для этого рассмотрим матрицу A системы уравнений-ограничений задачи.
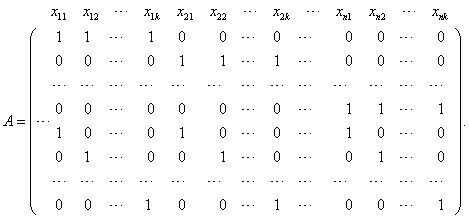
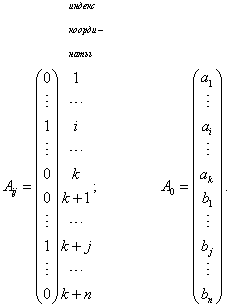
Таким образом в векторной форме задача будет выглядеть так:
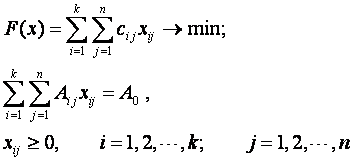
Пример. Составить математическую модель транспортной задачи, исходные данные которой приведены в таблице:
| | 20 | 30 | 40 |
| 40 |
3 | 5 |
7 |
| 50 | 4 | 6 | 10 |
Решение. Введем переменные задачи (матрицу перевозок)
| x11 | x12 | x13 |
|
x21 | x22 |
x23 |
Запишем матрицу стоимостей
Целевая функция задачи равна сумме произведений всех соответствующих элементов матриц С и X:
F(X )=3x 11 +5x 12 +7x13+4x21+6x22+10x23.
Данная функция, определяющая суммарные затраты на все перевозки, должна достигать минимального значения.
Составим систему ограничений задачи. Сумма всех перевозок, стоящих в первой строке матрицы X, должна равняться запасам 1-го поставщика, а сумма перевозок во второй строке матрицы X — запасам 2-го поставщика. Следовательно:
x11 + x 12 + x 13 = 40; и х21 + х22 + х23 = 50.
Это означает, что запасы поставщиков вывозятся полностью.
Суммы перевозок, стоящих в каждом столбце матрицы X, должны быть равны запросам соответствующих потребителей:
x11 + x 21 = 20;x 12 + x22= 30; и х31 + х32 = 40.
Это означает, что запросы потребителей удовлетворяются полностью.
Необходимо также учитывать, что перевозки не могут быть отрицательными:
х ij ≥ 0 , i = 1, 2, j= 1,2,3.
Следовательно, математическая модель рассматриваемой задачи такова: найти переменные задачи, обеспечивающие минимум функции:
F(X)=3·x11+5·x12+7·x31+4·x21+6·x22+10·x23
и удовлетворяющие системе ограничений
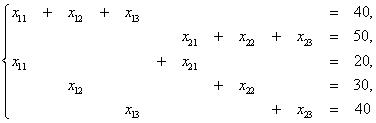
Необходимое и достаточное условия разрешимости транспортной задачи
Теорема. Для того чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей:
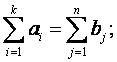
т.е. задача должна быть с правильным балансом.
Доказательство . Необходимость. Пусть задача имеет допустимое решение
X0=(x0ij), x0ij≥0, i=1,2,...,k; n=1,2,...,n
Докажем, что 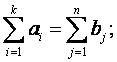. Подставив
X0 в уравнения системы ограничений (6.2), (6.3), получим
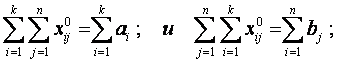
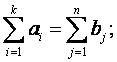
Достаточность. Пусть задача имеет правильный баланс
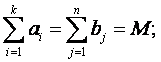
Докажем, что в этом случае задача имеет оптимальное решение.
Сначала покажем, что область допустимых решений задачи – непустое множество. Легко проверить, что
Далее покажем, что существует оптимальное решение. Учитывая, что стоимости перевозок единиц груза ограничены сверху и снизу C≤cij≤ D; i=1,2,…,k; j=1,2,…,n, где C и D — конечные постоянные, можно записать
Свойство системы ограничений транспортной задачи
Теорема. Ранг системы векторов-условий транспортной задачи равен N = k+ n- 1. Доказательство. Как известно из линейной алгебры для нахождения базиса системы векторов A1А2, ..., Аn необходимо составить однородную систему уравненийA1 x 1 +А2x 2 + ... Аnx 2 = θ.
(здесь θ - нулевой вектор)
Эту систему с помощью преобразований Жордана приводят к равносильной разрешенной; в базис включают векторы, соответствующие разрешенным неизвестным. Ранг системы векторов равен числу векторов, входящих в базис, т.е. числу разрешенных неизвестных этой системы. Системе векторов-условий транспортной задачи Aij., i = 1, 2, ..., k; j = 1, 2, ..., n соответствует однородная система уравнений
где θ = (0, 0, ..., 0) T — нулевой вектор (транспонированный).
Запишем матрицу этой системы (она является также матрицей системы ограничений транспортной задачи):
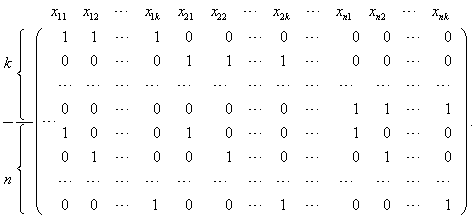
Покажем, что найдутся N = k + n - 1 линейно независимых векторов-условий. Из векторов-условий задачи выберем следующие:
A 1 n А2 n , ..., АknA 11 А12, ..., А1( n -1) и убедимся, что они линейно независимы. Для этого составим систему уравнений
A1n x 1 n+А2nx2n+…+ Aknxkn +А12x 12 + ... А1(n-1)x 1( n -1) = θ.
Матрица этой системы, как легко показать, приводится к единичной. Следовательно система уравнений имеет единственное нулевое решение x1n= x2n= … = xkn = x11= x12=…= x1(n-1)=0,а система векторов линейно независима. Теорема доказана.
Для решения транспортной задачи можно воспользоваться средствами MS Excel или калькулятором.
Распределительный метод
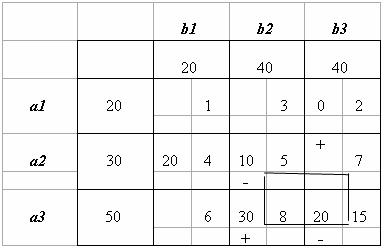
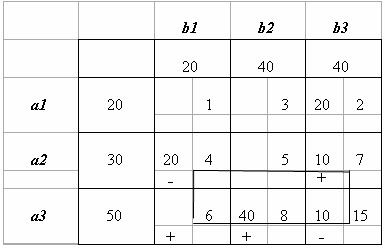
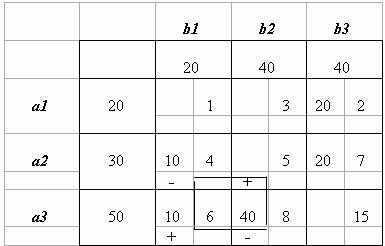
Один из наиболее простых методов решения транспортных задач - распределительный метод.Пусть для транспортной задачи найдено начальное опорное решение Х1 и вычислено значение целевой функции на этом решении F(Х1). По доказанной выше теореме для каждой свободной клетки таблицы задачи можно построить единственный цикл, который содержит эту клетку и часть клеток, занятых опорным решением. Обозначив этот цикл и осуществив сдвиг (перераспределение груза) по циклу на величину
можно получить новое опорное решение Х2.
Определим, как изменится целевая функция при переходе к новому опорному решению. При сдвиге на единицу груза по циклу, соответствующему клетке (l,m), приращение целевой функции Δlm равно разности двух сумм:
- сумма стоимостей перевозок единиц груза в нечетных клетках цикла, отмеченных знаком “+” ; 
- сумма стоимостей перевозок единиц груза в четных клетках цикла, отмеченных знаком “-”.
В клетках, отмеченных знаком “+”, величины груза прибавляются, что приводит к увеличению значения целевой функции F(X), а в клетках, отмеченных знаком “-”, величины груза уменьшаются, что приводит к уменьшению значения целевой функции.
Если разность сумм для свободной клетки ( l, m ) меньше нуля, т.е. Δ lm< 0, то перераспределение величины θ по соответствующему циклу приведет к уменьшению значения F(X) на величину θ•Δlm, т.е. опорное решение можно улучшить. Если же величины Δlm, называемые оценками, для всех свободных клеток таблицы транспортной задачи неотрицательны, то значение целевой функции нельзя уменьшить и опорное решение оптимально. Следовательно, признаком оптимальности распределительного метода является условие
Δlm≥0, ∀xlm=0
Для решения транспортной задачи распределительным методом необходимо найти начальное опорное решение. Затем для очередной опорной клетки (l, m) построить цикл и вычислить оценку Δlm. Если оценка неотрицательная, переходят к следующей свободной клетке. Если же оценка отрицательная, следует осуществить сдвиг по циклу на величину θ=min{xij}. В результате получится новое опорное решение.
Для каждого нового опорного решения вычисление оценок начинается с первой свободной клетки таблицы. Очередность проверяемых свободных клеток целесообразно устанавливать в порядке возрастания стоимости перевозок cij ,так как решается задача на нахождение минимума.
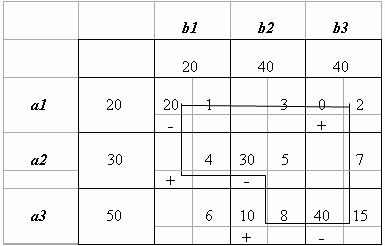
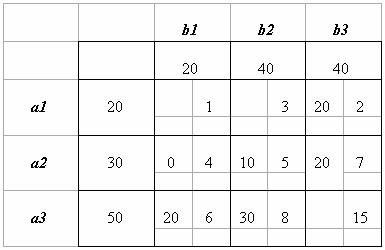
Пример. Решить распределительным методом транспортную задачу, исходные данные которой приведены в таблице:
| b1 | b2 | b3 | |||||
| 20 | 40 | 40 | |||||
| a1 | 20 | 1 | 3 | 2 | |||
| a2 | 30 | 4 | 5 | 7 | |||
| a3 | 50 | 6 | 8 | 15 | |||
Решение. Строим начальное опорное решение методом минимальной стоимости :
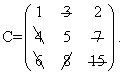
Затем вычисляем значение целевой функции на нем: F(X1) = 20·1 + 30·5 + 10·8 + 40·15 = 850.
Таблица
