Метод Фогеля
Данный метод состоит в следующем:- на каждой итерации находят разности между двумя наименьшими тарифами во всех строках и столбцах, записывая их в дополнительные столбец и строку таблицы;
- находят максимальную разность и заполняют клетку с минимальной стоимостью в строке (столбце), которой соответствует данная разность.
Графический метод решения ЗЛП
Симплексный метод решения ЗЛП
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Задачи динамического программирования
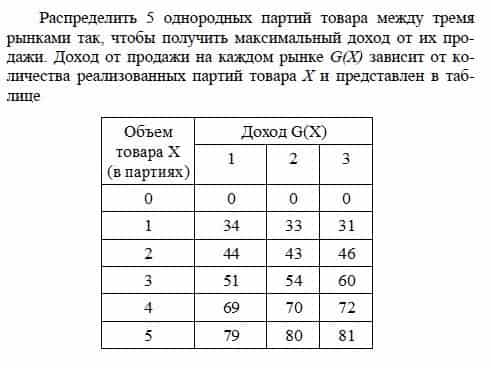
Как правило, опорный план, получаемый с помощью метода Фогеля, является сразу оптимальным (как в примере №2), но иногда приходиться применять и метод потенциалов для его улучшения (пример №1).
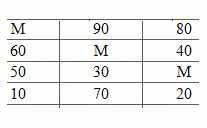
Пример №1. Ниже приведены числовые данные транспортных задач. Стоимость перевозки единицы продукции записаны в клетках таблицы. Запасы указаны справа от таблиц, а потребности – снизу. Из каждого плана найти оптимальный план методом потенциалов.
Решение:
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов.
| 1 | 2 | 3 | 4 | 5 | Запасы | |
| 1 | 9 | 5 | 7 | 10 | 18 | 78 |
| 2 | 36 | 29 | 6 | 38 | 40 | 94 |
| 3 | 41 | 20 | 11 | 25 | 19 | 29 |
| 4 | 30 | 28 | 13 | 39 | 50 | 86 |
| Потребности | 49 | 60 | 78 | 50 | 50 |
Проверим необходимое и достаточное условие разрешимости задачи.
∑ a = 78 + 94 + 29 + 86 = 287
∑ b = 49 + 60 + 78 + 50 + 50 = 287
Занесем исходные данные в распределительную таблицу.
| 1 | 2 | 3 | 4 | 5 | Запасы | |
| 1 | 9 | 5 | 7 | 10 | 18 | 78 |
| 2 | 36 | 29 | 6 | 38 | 40 | 94 |
| 3 | 41 | 20 | 11 | 25 | 19 | 29 |
| 4 | 30 | 28 | 13 | 39 | 50 | 86 |
| Потребности | 49 | 60 | 78 | 50 | 50 |
1. Используя метод Фогеля, построим первый опорный план транспортной задачи.
1. Для каждой строки и столбца таблицы условий найдем разности между двумя минимальными тарифами, записанными в данной строе или столбце, и поместим их в соответствующем дополнительном столбце или строке.
Первый минимальный элемент строки N=1 равен 5. Второй минимальный элемент строки N=1 равен 7. Разность равна 2.
Первый минимальный элемент строки N=2 равен 6. Второй минимальный элемент строки N=2 равен 29. Разность равна 23.
Первый минимальный элемент строки N=3 равен 11. Второй минимальный элемент строки N=3 равен 19. Разность равна 8.
Первый минимальный элемент строки N=4 равен 13. Второй минимальный элемент строки N=4 равен 28. Разность равна 15.
Первый минимальный элемент столбца N=1 равен 9. Второй минимальный элемент столбца N=1 равен 30. Разность равна 21.
Первый минимальный элемент столбца N=2 равен 5. Второй минимальный элемент столбца N=2 равен 20. Разность равна 15.
Первый минимальный элемент столбца N=3 равен 6. Второй минимальный элемент столбца N=3 равен 7. Разность равна 1.
Первый минимальный элемент столбца N=4 равен 10. Второй минимальный элемент столбца N=4 равен 25. Разность равна 15.
Первый минимальный элемент столбца N=5 равен 18. Второй минимальный элемент столбца N=5 равен 19. Разность равна 1.
Вычислив все эти разности, видим, что наибольшая из них соответствует строке (2). В этой строке минимальный тариф записан в клетке, находящейся на пересечении строки (2) и столбца (3).
| 1 | 2 | 3 | 4 | 5 | Запасы | Разности по строкам | |
| 1 | 9 | 5 | 7 | 10 | 18 | 78 | 2 |
| 2 | 36 | 29 | 6 | 38 | 40 | 94 | 23 |
| 3 | 41 | 20 | 11 | 25 | 19 | 29 | 8 |
| 4 | 30 | 28 | 13 | 39 | 50 | 86 | 15 |
| Потребности | 49 | 60 | 78 | 50 | 50 | 0 | 0 |
| Разности по столбцам | 21 | 15 | 1 | 15 | 1 | 0 |
Первый минимальный элемент строки N=2 равен 29. Второй минимальный элемент строки N=2 равен 36. Разность равна 7.
Первый минимальный элемент строки N=3 равен 19. Второй минимальный элемент строки N=3 равен 20. Разность равна 1.
Первый минимальный элемент строки N=4 равен 28. Второй минимальный элемент строки N=4 равен 30. Разность равна 2.
Первый минимальный элемент столбца N=1 равен 9. Второй минимальный элемент столбца N=1 равен 30. Разность равна 21.
Первый минимальный элемент столбца N=2 равен 5. Второй минимальный элемент столбца N=2 равен 20. Разность равна 15.
Первый минимальный элемент столбца N=4 равен 10. Второй минимальный элемент столбца N=4 равен 25. Разность равна 15.
Первый минимальный элемент столбца N=5 равен 18. Второй минимальный элемент столбца N=5 равен 19. Разность равна 1.
Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу (1). В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки (1) и столбца (1).
| 1 | 2 | 3 | 4 | 5 | Запасы | Разности по строкам | |
| 1 | 9 | 5 | 7 | 10 | 18 | 78 | 4 |
| 2 | 36 | 29 | 6 | 38 | 40 | 16 | 7 |
| 3 | 41 | 20 | 11 | 25 | 19 | 29 | 1 |
| 4 | 30 | 28 | 13 | 39 | 50 | 86 | 2 |
| Потребности | 49 | 60 | 0 | 50 | 50 | 0 | 0 |
| Разности по столбцам | 21 | 15 | - | 15 | 1 | 0 |
Первый минимальный элемент строки N=1 равен 5. Второй минимальный элемент строки N=1 равен 10. Разность равна 5.
Первый минимальный элемент строки N=2 равен 29. Второй минимальный элемент строки N=2 равен 38. Разность равна 9.
Первый минимальный элемент строки N=3 равен 19. Второй минимальный элемент строки N=3 равен 20. Разность равна 1.
Первый минимальный элемент строки N=4 равен 28. Второй минимальный элемент строки N=4 равен 39. Разность равна 11.
Первый минимальный элемент столбца N=2 равен 5. Второй минимальный элемент столбца N=2 равен 20. Разность равна 15.
Первый минимальный элемент столбца N=4 равен 10. Второй минимальный элемент столбца N=4 равен 25. Разность равна 15.
Первый минимальный элемент столбца N=5 равен 18. Второй минимальный элемент столбца N=5 равен 19. Разность равна 1.
Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу (4). В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки (1) и столбца (4).
| 1 | 2 | 3 | 4 | 5 | Запасы | Разности по строкам | |
| 1 | 9 | 5 | 7 | 10 | 18 | 29 | 5 |
| 2 | 36 | 29 | 6 | 38 | 40 | 16 | 9 |
| 3 | 41 | 20 | 11 | 25 | 19 | 29 | 1 |
| 4 | 30 | 28 | 13 | 39 | 50 | 86 | 11 |
| Потребности | 0 | 60 | 0 | 50 | 50 | 0 | 0 |
| Разности по столбцам | - | 15 | - | 15 | 1 | 0 |
Читать далее
4. Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0.
| v1=7 | v2=5 | v3=-16 | v4=10 | v5=18 | |
| u1=0 | 9 | 5[23] | 7 | 10[50] | 18[5] |
| u2=22 | 36 | 29 | 6[78] | 38 | 40[16] |
| u3=1 | 41 | 20 | 11 | 25 | 19[29] |
| u4=23 | 30[49] | 28[37] | 13 | 39 | 50 |
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vj <= cij.
Минимальные затраты составят: F( x) = 5*23 + 10*50 + 18*5 + 6*78 + 40*16 + 19*29 + 30*49 + 28*37 = 4870
Пример №2
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 5 | 2 | 1 | 8 | 10 |
| 2 | 2 | 1 | 2 | 3 | 10 |
| 3 | 4 | 8 | 1 | 4 | 20 |
| Потребности | 14 | 15 | 5 | 6 |
Проверим необходимое и достаточное условие разрешимости задачи.
∑a = 10 + 10 + 20 = 40
∑b = 14 + 15 + 5 + 6 = 40
Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
Занесем исходные данные в распределительную таблицу.
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 5 | 2 | 1 | 8 | 10 |
| 2 | 2 | 1 | 2 | 3 | 10 |
| 3 | 4 | 8 | 1 | 4 | 20 |
| Потребности | 14 | 15 | 5 | 6 |
Этап I. Поиск первого опорного плана.
1. Используя метод Фогеля, построим первый опорный план транспортной задачи. Для каждой строки и столбца таблицы условий найдем разности между двумя минимальными тарифами, записанными в данной строе или столбце, и поместим их в соответствующем дополнительном столбце или строке.
Данный метод состоит в следующем:
1. на каждой итерации находят разности между двумя наименьшими тарифами во всех строках и столбцах, записывая их в дополнительные столбец и строку таблицы;
2. находят максимальную разность и заполняют клетку с минимальной стоимостью в строке (столбце), которой соответствует данная разность.
Находим разности по строкам.
Для строки N=1 первый минимальный элемент min11= 1, второй минимальный элемент min21= 2. Их разность равна d = min21- min11= 1.
Для строки N=2 первый минимальный элемент min12= 1, второй минимальный элемент min22= 2. Их разность равна d = min22- min12= 1.
Для строки N=3 первый минимальный элемент min13= 1, второй минимальный элемент min23= 4. Их разность равна d = min23- min13= 3.
Находим разности по столбцам.
Для столбца N=1 первый минимальный элемент min11= 2. второй минимальный элемент min214. Их разность d = min21- min11= 2.
Для столбца N=2 первый минимальный элемент min12= 1. второй минимальный элемент min222. Их разность d = min22- min12= 1.
Для столбца N=3 первый минимальный элемент min13= 1. второй минимальный элемент min231. Их разность d = min23- min13= 0.
Для столбца N=4 первый минимальный элемент min14= 3. второй минимальный элемент min244. Их разность d = min24- min14= 1.
Вычислив все эти разности, видим, что наибольшая из них соответствует строке (3). В этой строке минимальный тариф записан в клетке, находящейся на пересечении строки (3) и столбца (3).
| 1 | 2 | 3 | 4 | Запасы | Разности по строкам | |
| 1 | 5 | 2 | 1 | 8 | 10 | 1 |
| 2 | 2 | 1 | 2 | 3 | 10 | 1 |
| 3 | 4 | 8 | 1 | 4 | 20 | 3 |
| Потребности | 14 | 15 | 5 | 6 | 0 | 0 |
| Разности по столбцам | 2 | 1 | 0 | 1 | 0 |
Искомый элемент равен 1
Для этого элемента запасы равны 20, потребности 5. Поскольку минимальным является 5, то вычитаем его.
x33= min(20,5) = 5.
| 0 | 0 | x | 0 | 0 |
| 0 | 0 | x | x | 0 |
| 0 | 0 | 0 | x | 20 - 5 = 15 |
| 0 | x | 5 - 5 = 0 | x | x |
Находим разности по строкам.
Для строки N=1 первый минимальный элемент min11= 2, второй минимальный элемент min21= 5. Их разность равна d = min21- min11= 3.
Для строки N=2 первый минимальный элемент min12= 1, второй минимальный элемент min22= 2. Их разность равна d = min22- min12= 1.
Для строки N=3 первый минимальный элемент min13= 4, второй минимальный элемент min23= 4. Их разность равна d = min23- min13= 0.
Находим разности по столбцам.
Для столбца N=1 первый минимальный элемент min11= 2. второй минимальный элемент min214. Их разность d = min21- min11= 2.
Для столбца N=2 первый минимальный элемент min12= 1. второй минимальный элемент min222. Их разность d = min22- min12= 1.
Для столбца N=4 первый минимальный элемент min14= 3. второй минимальный элемент min244. Их разность d = min24- min14= 1.
Вычислив все эти разности, видим, что наибольшая из них соответствует строке (1). В этой строке минимальный тариф записан в клетке, находящейся на пересечении строки (1) и столбца (2).
| 1 | 2 | 3 | 4 | Запасы | Разности по строкам | |
| 1 | 5 | 2 | 1 | 8 | 10 | 3 |
| 2 | 2 | 1 | 2 | 3 | 10 | 1 |
| 3 | 4 | 8 | 1 | 4 | 15 | 0 |
| Потребности | 14 | 15 | 0 | 6 | 0 | 0 |
| Разности по столбцам | 2 | 1 | - | 1 | 0 |
Искомый элемент равен 2
Для этого элемента запасы равны 10, потребности 15. Поскольку минимальным является 10, то вычитаем его.
x12= min(10,15) = 10.
| x | 0 | 0 | x | 10 - 10 = 0 |
| 0 | x | x | x | x |
| 0 | 0 | x | 0 | 0 |
| 0 | 15 - 10 = 5 | x | 0 | 0 |
Находим разности по строкам.
Для строки N=2 первый минимальный элемент min12= 1, второй минимальный элемент min22= 2. Их разность равна d = min22- min12= 1.
Для строки N=3 первый минимальный элемент min13= 4, второй минимальный элемент min23= 4. Их разность равна d = min23- min13= 0.
Находим разности по столбцам.
Для столбца N=1 первый минимальный элемент min11= 2. второй минимальный элемент min214. Их разность d = min21- min11= 2.
Для столбца N=2 первый минимальный элемент min12= 1. второй минимальный элемент min228. Их разность d = min22- min12= 7.
Для столбца N=4 первый минимальный элемент min14= 3. второй минимальный элемент min244. Их разность d = min24- min14= 1.
Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу (2). В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки (2) и столбца (2).
| 1 | 2 | 3 | 4 | Запасы | Разности по строкам | |
| 1 | 5 | 2 | 1 | 8 | 0 | - |
| 2 | 2 | 1 | 2 | 3 | 10 | 1 |
| 3 | 4 | 8 | 1 | 4 | 15 | 0 |
| Потребности | 14 | 5 | 0 | 6 | 0 | 0 |
| Разности по столбцам | 2 | 7 | - | 1 | 0 |
Искомый элемент равен 1
x22= min(10,5) = 5.
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | x | 0 | 10 - 5 = 5 |
| 0 | x | x | x | x |
| 0 | 5 - 5 = 0 | x | 0 | 0 |
Находим разности по строкам.
Для строки N=2 первый минимальный элемент min12= 2, второй минимальный элемент min22= 3. Их разность равна d = min22- min12= 1.
Для строки N=3 первый минимальный элемент min13= 4, второй минимальный элемент min23= 4. Их разность равна d = min23- min13= 0.
Находим разности по столбцам.
Для столбца N=1 первый минимальный элемент min11= 2. второй минимальный элемент min214. Их разность d = min21- min11= 2.
Для столбца N=4 первый минимальный элемент min14= 3. второй минимальный элемент min244. Их разность d = min24- min14= 1.
Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу (1). В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки (2) и столбца (1).
| 1 | 2 | 3 | 4 | Запасы | Разности по строкам | |
| 1 | 5 | 2 | 1 | 8 | 0 | - |
| 2 | 2 | 1 | 2 | 3 | 5 | 1 |
| 3 | 4 | 8 | 1 | 4 | 15 | 0 |
| Потребности | 14 | 0 | 0 | 6 | 0 | 0 |
| Разности по столбцам | 2 | - | - | 1 | 0 |
Искомый элемент равен 2
x21= min(5,14) = 5.
| 0 | 0 | 0 | 0 | 0 |
| 0 | x | 0 | x | 5 - 5 = 0 |
| 0 | x | x | x | x |
| 14 - 5 = 9 | x | 0 | 0 | 0 |
Находим разности по строкам.
Для строки N=3 первый минимальный элемент min13= 4, второй минимальный элемент min23= 4. Их разность равна d = min23- min13= 0.
Находим разности по столбцам.
Для столбца N=1 первый минимальный элемент min11= 4. второй минимальный элемент min214. Их разность d = min21- min11= 0.
Для столбца N=4 первый минимальный элемент min14= 4. второй минимальный элемент min244. Их разность d = min24- min14= 0.
Вычислив все эти разности, видим, что наибольшая из них соответствует строке (3). В этой строке минимальный тариф записан в клетке, находящейся на пересечении строки (3) и столбца (1).
| 1 | 2 | 3 | 4 | Запасы | Разности по строкам | |
| 1 | 5 | 2 | 1 | 8 | 0 | - |
| 2 | 2 | 1 | 2 | 3 | 0 | - |
| 3 | 4 | 8 | 1 | 4 | 15 | 0 |
| Потребности | 9 | 0 | 0 | 6 | 0 | 0 |
| Разности по столбцам | 0 | - | - | 0 | 0 |
Искомый элемент равен 4
x31= min(15,9) = 9.
| 0 | 0 | 0 | 0 | 0 |
| 0 | x | 0 | 0 | 0 |
| 0 | x | 0 | 0 | 15 - 9 = 6 |
| 9 - 9 = 0 | x | x | x | x |
Находим разности по строкам.
Для строки N=3 первый минимальный элемент min13= 4, второй минимальный элемент min23= 4. Их разность равна d = min23- min13= 0.
Находим разности по столбцам.
Для столбца N=4 первый минимальный элемент min14= 4. второй минимальный элемент min244. Их разность d = min24- min14= 0.
Вычислив все эти разности, видим, что наибольшая из них соответствует строке (3). В этой строке минимальный тариф записан в клетке, находящейся на пересечении строки (3) и столбца (4).
| 1 | 2 | 3 | 4 | Запасы | Разности по строкам | |
| 1 | 5 | 2 | 1 | 8 | 0 | - |
| 2 | 2 | 1 | 2 | 3 | 0 | - |
| 3 | 4 | 8 | 1 | 4 | 6 | 0 |
| Потребности | 0 | 0 | 0 | 6 | 0 | 0 |
| Разности по столбцам | - | - | - | 0 | 0 |
Искомый элемент равен 4
x34= min(6,6) = 6.
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | x |
| 0 | 0 | 0 | 0 | 6 - 6 = 0 |
| 0 | x | x | 6 - 6 = 0 | x |
| 1 | 2 | 3 | 4 | Запасы | |
| 1 | 5 | 2[10] | 1 | 8 | 10 |
| 2 | 2[5] | 1[5] | 2 | 3 | 10 |
| 3 | 4[9] | 8 | 1[5] | 4[6] | 20 |
| Потребности | 14 | 15 | 5 | 6 |
Сведем все вычисления в одну таблицу.
| 1 | 2 | 3 | 4 | Запасы | d1 | d2 | d3 | d4 | |
| 1 | 5 | 2[10] | 1 | 8 | 10 | 1 | 3 | - | - |
| 2 | 2[5] | 1[5] | 2 | 3 | 10 | 1 | 1 | 1 | 1 |
| 3 | 4[9] | 8 | 1[5] | 4[6] | 20 | 3 | 0 | 0 | 0 |
| Потребности | 14 | 15 | 5 | 6 | |||||
| d1 | 2 | 1 | 0 | 1 | |||||
| d2 | 2 | 1 | - | 1 | |||||
| d3 | 2 | 7 | - | 1 | |||||
| d4 | 2 | - | - | 1 |
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.
2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 6. Следовательно, опорный план является невырожденным.
Значение целевой функции для этого опорного плана равно:
F(x) = 2*10 + 2*5 + 1*5 + 4*9 + 1*5 + 4*6 = 100
Этап II. Улучшение опорного плана.
Проверим оптимальность опорного плана. Найдем предварительные потенциалыui, vj. по занятым клеткам таблицы, в которых ui+ vj= cij, полагая, что u1= 0.
u1+ v2= 2; 0 + v2= 2; v2= 2
u2+ v2= 1; 2 + u2= 1; u2= -1
u2+ v1= 2; -1 + v1= 2; v1= 3
u3+ v1= 4; 3 + u3= 4; u3= 1
u3+ v3= 1; 1 + v3= 1; v3= 0
u3+ v4= 4; 1 + v4= 4; v4= 3
| v1=3 | v2=2 | v3=0 | v4=3 | |
| u1=0 | 5 | 2[10] | 1 | 8 |
| u2=-1 | 2[5] | 1[5] | 2 | 3 |
| u3=1 | 4[9] | 8 | 1[5] | 4[6] |
Минимальные затраты составят: F(x) = 2*10 + 2*5 + 1*5 + 4*9 + 1*5 + 4*6 = 100
Анализ оптимального плана.
Из первого склада необходимо весь груз направить в второй магазин
Из 2-го склада необходимо груз направить в 1-й магазин (5), в 2-й магазин (5)
Из третьего склада необходимо груз направить в 1-й магазин (9), в третий магазин (5), в 4-й магазин (6).