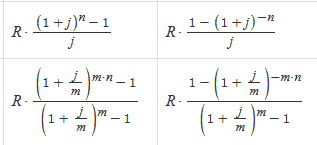Определитель матрицы ▦ Производная функции dydx График 3D Упростить выражение Графический метод решения задач нелинейного программирования ⇲ …
Примеры решений Метод Гомори Симплекс-метод Метод Фогеля Транспортная задача 🚚 Задача о назначениях Распределительный метод Метод потенциалов Задача коммивояжера Открытые и закрытые задачи

Транспортная задача с ограничениями на пропускную способность

Инструкция. Для получения онлайн решения транспортной задачи выберите размерность матрицы тарифов.
Количество столбцов (магазины)
Количество строк (поставщики)
Здесь будет отображаться решение.
Найти решение транспортной задачи, если из А2 в В4 перевозки запрещены, из А1 в В3 должно быть доставлено не менее n единиц груза, а из А3 в В1 не более m единиц груза.

Пусть требуется при решении транспортной задачи ограничить перевозки от поставщика с номером l к потребителю с номером m.
Возможны ограничения двух типов:

  1. xlm > а;
  2. xlm < b,
  3. xlm = k,
где а и b- постоянные величины.

1. Если xlm > a, то необходимо прежде, чем решать задачу, сократить (уменьшить) запасы l-го поставщика и запросы m-го потребителя на величину а (зарезервировать перевозку xlm = а). После решения задачи в оптимальном решении следует увеличить объем перевозки xlm на величину а.

2. Если xlm<b, то необходимо вместо m-го потребителя с запросами bm ввести двух других потребителей. Один из них с номером m должен иметь запросы b 'm=b, а другой с номером п + 1- запросы bп+1= bm - b. Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости cl(n+1) которая принимается равной сколь угодно большому числу М (М >> 1). После получения оптимального решения величины грузов, перевозимых к (n + 1)-му потребителю, прибавляются к величинам перевозок l-го потребителя. Так как cl(n+1)) = М - самая большая стоимость перевозки, то в оптимальном решении клетка с номером (l, n+ 1) останется пустой, xl{n+1) = 0 и объем перевозки хlm не превзойдет b.

3. Если xlm = k, то необходимо уменьшить запасы и потребности для номеров l и m на величину k. Стоимость перевозки clm назначают равной М >> 1.

4. В некоторых задачах требуется запретить перевозки от отдельных поставщиков отдельным потребителям. В таких случаях либо зачеркивают соответствующую клетку таблицы транспортной задачи, либо назначают соответствующую этой клетке стоимость перевозки единицы груза сколь угодно большой, равной М >> 1. В остальном задача решается обычным способом.

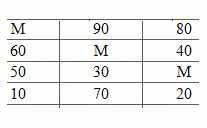
Пример. В трех хранилищах горючего ежедневно хранится 175, 125 и 140 т бензина. Этот бензин ежедневно получают четыре заправочные станции в количествах, равных соответственно 180, 110, 90 и 40 т. Тарифы перевозок 1 т бензина с хранилищ к заправочным станциям задаются матрицей .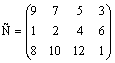
Составит такой план перевозок бензина, при котором общая стоимость перевозок является минимальной.

Рассмотрим первый вариант ограничения. Пусть требуется ограничить перевозки от поставщика с номером 2 к потребителю с номером 3 в размере не менее 40. Сокращаем запасы 2-го поставщика и запросы 3-го потребителя на величину а = 40. Решаем задачу с использованием калькулятора.

1 2 3 4 Запасы
1 9 7 5 3 175
2 1 2 4 6 85
3 8 10 12 1 40
Потребности 180 110 50 40

В результате получим оптимальный план.
1 2 3 4 Запасы
11511050
 175
285

 85
3


 40 40
4 80


 80
Потребности 180 110 50 40

Далее в оптимальном решении следует увеличить объем перевозки x23 на величину а = 40.
1 2 3 4 Запасы
11511050
 175
285 40

125
3


 40 40
4 80


 80
Потребности 180 11090 40

Рассмотрим второй вариант ограничения. Пусть требуется ограничить перевозки от поставщика с номером 2 к потребителю с номером 3 в размере не более 30. Вместо 3-го потребителя с запросами 90 вводим двух других потребителей. Один из них с номером 3 должен иметь запросы b'3=30, а другой с номером 4 + 1 - запросы b5 = 90 - 30 = 60. Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости c25 которая принимается равной сколь угодно большому числу М (М >> 1).

1 2 3 4 5 Запасы
1 9 7 5 3 5 175
2 1 2 4 6 - 125
3 8 10 12 1 12 140
Потребности 180 110 30 40 60

В результате получим опорный план.
  1 2 3 4 5 Запасы
1 9 7[85] 5[30] 3 5[60] 175
2 1[100] 2[25] 4 6 36 125
3 8[80] 10 12 1[40] 12 140
Потребности 180 110 30 40 60  

После получения оптимального решения величины грузов, перевозимых к 5-му потребителю, прибавляются к величинам перевозок 2-го потребителя. Так как c25 = М - самая большая стоимость перевозки, то в оптимальном решении клетка с номером (2, 5) останется пустой, x25 = 0 и объем перевозки х23 не превзойдет b = 30.
  1 2 3 4 Запасы
1   85 30+60   175
2 100 25 0 < 30   125
3 80     40 140
Потребности 180 110 90 40  

Рассмотрим третий вариант ограничения. x23 = 20. Модифицируем исходную матрицу:

1234Запасы
19753175
212M685-20=65
381012140
Потребности18011050-20=3040

Решая методом потенциалов, получаем следующий оптимальный план:
1234Запасы
19[35]7[110]5[30]3175
21[65]236665
38[0]10121[40]40
40[80]00080
Потребности1801103040

Восстанавливаем исходную матрицу:
1234Запасы
13511030 175
265 20 85=65+20
3 4040
48000080
Потребности18011050=30+2040

Пример №1. Транспортная задача с дополнительными ограничениями.
Скачать решение

Пример №2. Найти оптимальный план транспортной задачи, описываемой соответствующей таблицей, удовлетворяющим указанным условиям.

  1. Потребности пунктов B1 и B3 удовлетворяются полностью.
  2. Остаток груза в пункте A1 не менее 10 ед., но не более 13 ед.
  3. Суммарная вывозка из пунrта А1 не менее 45 ед.
  4. Суммарная поставка в пункт В1 не более 70
  5. Суммарная поставка в пункт В2 не менее 100
  6. В пункт В2 должно быть завезено не менее 25 ед.
  7. От второго поставщика должно быть вывезено не менее 50 ед.
  8. x12 ≤ 15
  9. Суммарная вывозка из всех пунктов равна 75 ед.
  10. Должен быть вывезен весь груз из пунктов А3 и А2.
  11. Суммарная поставка в пункт В2 не превосходит 50 ед., груза, но не менее 35 ед.
  12. Из пункта А1 нужно вывезти не менее 160 ед. груза, а в пункт В1 завезти  не менее 70 ед. груза из пункта А2.
  13. x11 + x21 ≤ 35