Метод идеальной точки
Метод идеальной точки заключается в нахождении на границе Парето точки, ближайшей к точке утопии. Обычно эта точка не реализуется при заданных ограничениях, поэтому ее и называют точкой утопии.Назначение сервиса. С помощью данного сервиса можно в онлайн режиме решить многокритериальную задачу с двумя целевыми функциями.
1 ≤ x1 ≤ 4, то оно разбивается на два: x1 ≥ 1, x1 ≤ 4 (т.е. количество строк увеличивается на 1).
Симплексный метод решения ЗЛП
Решение транспортной задачи
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Применение метода идеальной точки
Дадим подробную иллюстративную характеристику применения метода идеальной точки к конкретным задачам оптимизации с двумя целевыми функциями. Это позволит не приводить последующего его формального описания.Пример 1. Найти значения переменных, при которых функции
L1=2x1+x2+1→ max;
L2= x1-x2+5→ max
при ограничениях:
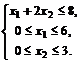
Решение. Введем на плоскости прямоугольную систему координат Ox1x2 и построим множество X — область допустимых решений данной задачи в указанной системе координат. Ограничительные условия определяют на плоскости многоугольник ABCDE (Рис. 1), вершины которого имеют соответственно координаты: (0; 0), (0; 3), (2; 3), (6; 1), (6; 0). Следовательно, X представляет собою многоугольник ABCDE.
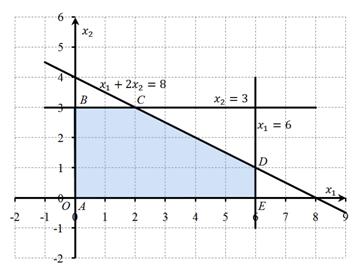
Рис. 1. Область допустимых решений на плоскости Ox1x2
Подвергнем координаты каждой точки плоскости Ox1x2 преобразованиям L1=2x1+x2+1 и L2= x1-x2+5. Получим плоскость OL1L2. При этом в силу линейности проводимых преобразований прямоугольная система координат Ox1x2 перейдет в прямоугольную систему координат OL1L2, а многоугольник ABCDE в многоугольник A*B*C*D*E*, вершины которого имеют соответственно координаты: (1; 5), (4; 2), (8; 4), (14; 10), (13; 11) (рис. 2). Для наглядности укажем описанное соответствие вершин: A(0; 0) → A*(1; 5), B(0; 3) → B*(4; 2), C(2; 3) → C*(8; 4), D(6; 1) → D*(14; 10), E(6; 0) → E*(13; 11).
Таким образом, все точки, координаты которых удовлетворяют условиям L1=2x1+x2+1, L2= x1-x2+5 и (x1, x2) ∈ X, определяют на плоскости многоугольник A*B*C*D*E*. Следовательно, область допустимых решений L данной задачи в системе координат OL1L2 (пространстве критериев) представляет собою многоугольник A*B*C*D*E*.
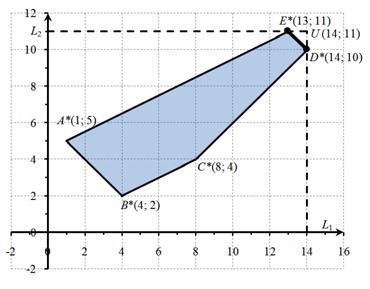
Рис. 2. ОДР в пространстве критериев и множество Парето
Находим множество Парето. Это отрезок D*E*. В условии задачи не сказано, что считать точкой утопии. Поэтому выбираем комбинацию наилучших значений всех критериев. В данном случае это точка U с координатами (14; 11).
Теперь необходимо найти во множестве Парето точку, расположенную ближе всех к точке утопии U. Из рис. 2 видно, что точка I(I1,I2), являющаяся основанием перпендикуляра, проведенного из точки U (14; 11) к прямой D*E*, принадлежит отрезку D*E*. Это означает, что точка I — искомая. Найдем ее координаты.
Воспользуемся уравнением прямой, проходящей через две заданные точки. Имеем
,
где L1D*, L2D* и L1E*, L2E* — координаты точек D* и E* соответственно. Подставляя сюда числовые значения для координат D* и E*, находим:
, или L1+L2=24.
Нормальным вектором прямой D*E* является вектор N(1; 1), направляющим вектором для прямой UI. Следовательно, ее каноническое уравнение имеет вид:
,
где L1U, L2U — координаты точки U. Подставляя сюда числовые значения для координат U, находим:
, или L1-L2=3.
Точка I принадлежит прямым D*E* и UI (рис. 3). Поэтому ее координаты удовлетворяют системе уравнений
Отсюда находим L1=27/2, L2=21/2.
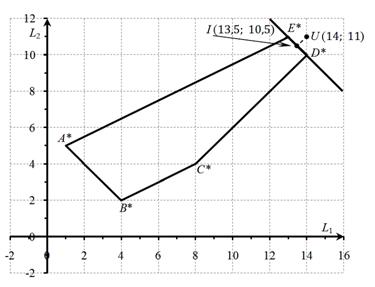
Рис. 3. Идеальная точка
Расстояние d между точками I(27/2; 21/2) и U(14; 11) равно длине вектора U = (14-27/2; 11-21/2) = (½ ; ½), которая, в свою очередь, равна корню квадратному из суммы квадратов его координат. Поэтому 
Соответствующие значения x1, x2 найдем из системы линейных уравнений
Имеем x1=6, x2=½
Таким образом, Парето-оптимальное решение L1=27/2, L2=21/2 достигается при x1=6, x2=½, а идеальная точка (27/2; 21/2) находится от точки утопии (14; 11) на расстоянии 
.
и идеальной точкой, учитывая топологию множества Парето, был применен «геометрический» метод. В общем случае задача нахождения расстояния между указанными точками решается как экстремальная. Необходимо найти на множестве Парето точку, такую, что расстояние между ней и точкой утопии минимально:
→ min, или, опуская знак квадратного корня,
→ min,
где I1 и I2 — неизвестные координаты искомой точки I, а U1 и U1 — уже найденные координаты точки утопии U.
Пример 2. Найти значения переменных, при которых функции
L1=2x1+x2+1→ max;
L2= x1-x2+5→ min
при тех же ограничениях, что и в примере 1.
Решение. Введем функцию L2’= -x1+x2-5. Тогда, согласно замечанию 1, исходная задача преобразуется в задачу максимизации
L1=2x1+x2+1→ max;
L2’= -x1+x2-5→ max.
Рис. 4. Геометрическая интерпретация задачи максимизации
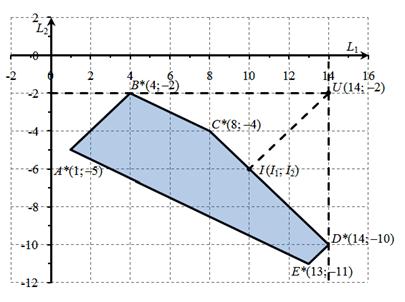
Ограничительные условия те же, что и в примере 1. Они определяют на плоскости Ox1x2 многоугольник ABCDE (рис. 1), который функции L1=2x1+x2+1 и L2’= -x1+x2-5 переводят в многоугольник A*B*C*D*E*. Еговершины в плоскости OL1L2’ (пространстве критериев) имеют соответственно координаты: (1; -5), (4;-2), (8;-4), (14; -10), (13; -11) (рис. 4).
Множество Парето образуют точки ломаной B*C*D*. Как и в примере 1, в условии не сказано, что считать точкой утопии. Поэтому снова выбираем комбинацию наилучших значений всех критериев. В данном случае это точка U с координатами (14;-2) (заметим, что в исходной задаче ей соответствует точка с координатами (14;2), и, следовательно, в исходной задаче точкой утопии является она). Из рис. 4 видно, что точка, принадлежащая ломаной B*C*D* и находящаяся на минимальном расстоянии от точки утопии, должна принадлежать отрезку C*D*. Обозначим ее через I(I1; I2). Для отыскания ее координат воспользуемся способом, описанным в замечании 2. Согласно этому способу, нужно минимизировать функцию расстояния d между точкой I(I1; I2) и точкой U(14;-2):
→ min,
или
→ min.
Составим уравнение прямой C*D* (подробности см. в примере 1). Имеем
, или L1+L2’=4.
Точка Iпринадлежит множеству точек отрезка C*D*.Следовательно, ее координаты удовлетворяют уравнению прямой C*D*: I1+I2= 4, или I1=I2+4. Это означает, что минимизируется функция y=2(I2)2+24I2+104 на отрезке [-10;-4]. Вычисляем производную y′=4I2+24 и находим стационарную точку: I2=-6. Легко видеть, что y’<0 на промежутке [-10;-6) и y’>0 на промежутке (-6; -4]. Следовательно, (-6) — точка минимума функции y(I2) на отрезке [-10;-4], а (10;-6) — точка минимума функции y(I1, I2) = (-I1-10)2+(I2+2)2 в замкнутой области, определяемой неравенствами 8≤I1≤14 и -10≤I2≤-4, при этом dmin=d(10;-6) =
. Заметим, что в исходной задаче точке (10;-6) соответствует точка (10; 6).
Соответствующие значения x1, x2 найдем из системы линейных уравнений
Имеем x1 =10/3, x2=7/3
Таким образом, Парето-оптимальное решение L1=10, L2=6 достигается при x1 =10/3, x2=7/3. При этом идеальная точка (10;6) находится от точки утопии (14;2) на расстоянии
.
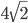Пример решения экономической задачи с двумя критериями эффективности
В качестве примера рассмотрим конкретную задачу из практики действующего предприятия (задачу регионального уровня).Задача 1. ОАО «Мукомольный завод „Балашовский“» реализует хлебопекарную муку высшего сорта двумя способами: через сеть магазинов и через прямые поставки по договорам неторговым организациям. Известно, что ежемесячно магазины могут реализовать не более 50 тыс., а ежемесячные поставки неторговым организациям не должны превышать 35 тыс. т муки. Для продажи в каждом месяце выделяется не более 45 тыс. т муки. Предприятие выработало определенную политику в области ценообразования, которой собиралось следовать. Однако в связи с сильно изменившейся экономической ситуацией, затраты на реализацию увеличились, а мука вошла в перечень продуктов, которые должны продаваться по ранее установленной цене, регулируемой местной властью. При продаже одной тонны муки через магазины расходы на реализацию стали составлять 7 тыс. руб., а цена осталась прежней — 10 тыс. руб.; при втором способе реализации расходы и цена составили 4 и 6 тыс. руб. соответственно. Необходимо определить, сколько тонн муки следует продавать каждым способом, чтобы расходы были минимальными, а выручка от продажи — максимальной.
Решение. Составим математическую модель задачи.
Пусть x1 и x2 — объемы (тысячи тонн) реализуемой в ноябре хлебопекарной муки высшего сорта через сеть магазинов и через прямые поставки по договорам неторговым организациям соответственно.
Тогда целевые функции имеют вид:
L1=7x1+5x2→ min;
L2=10x1+8x2→ max
при ограничениях:
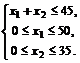
Введем функцию L1’= -7x1-5x2. Тогда исходная задача преобразуется в задачу максимизации
L1’= -7x1-5x2→ max;
L2=10x1+8x2→ max.
Ограничительные условия остаются прежними. Они определяют на плоскости Ox1x2 многоугольник ABCD (рис. 5), который функции L1’ и L2 переводят в многоугольник A*B*C*D* плоскости OL1’ L2:
A(0; 0) → A*(0; 0), B(0; 35) → B*(–175; 280),
C(10; 35) → C*(–245; 380), D(45; 0) → D*(–315; 450) (Рис. 5).
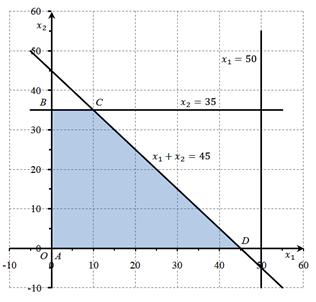
Рис. 5. ОДР на плоскости Ox1x2
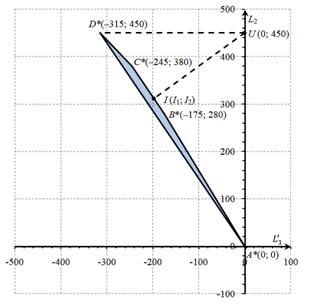
Рис. 6. Геометрическая интерпретация задачи максимизации, эквивалентной задаче 1
Множество Парето образуют точки ломаной A*B*C*D*. Выбираем комбинацию наилучших значений всех критериев. В данном случае это точка U с координатами (0;450). Необходимо найти во множестве Парето точку, расположенную ближе всех к точке утопии U. Обозначим ее через I(I1; I2). Для отыскания координат указанной точки минимизируем функцию расстояния d между точкой I(I1; I2) и точкой U(0;415):
→ min,
или
y=I21+(I2-450) → min.
Из рис. 6 видно, что искомая точка находится на отрезке B*C*.
Составим уравнение прямой B*C*. Имеем
, или 10L1’+7L2=210.
Точка Iпринадлежит множеству точек отрезка B*C*. Следовательно, ее координаты удовлетворяют уравнению прямой B*C*: 10L1’+7L2=210, или
. Это означает, что на отрезке [-245;-175] минимизируется функция 
. Вычисляем производную 
и находим стационарную точку: 
. Из того, что y’<0 на промежутке [–245; 
) и y’>0 на промежутке (; –175], следует: 
— точка минимума функции y(I1) на отрезке [-245;-175]. Тогда 
— искомая точка, что соответствует точке 
в исходной задаче.
Соответствующие значения x1,x2 найдем из системы линейных уравнений
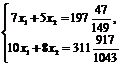
Имеем x1=3 196/1043, x2=35
Таким образом, объемы реализации хлебопекарной муки высшего сорта ОАО «Мукомольный завод „Балашовский“» должны составить: ≈ 3,19 тыс. т через сеть магазинов и 35 тыс. т через прямые поставки по договорам неторговым организациям. При таких способах и объемах реализации расходы будут минимальными (составят ≈ 197,32 тыс. руб.), а выручка — максимальной (составит ≈ 311,88 тыс. руб.).
Пример 3. Фирма имеет возможность реализовывать свои товары на 4-х различных рынках. Затраты на рекламу на этих рынках составляют соответственно 7, 5, 9, и 6 тыс. денежных единиц, доля рынка - 45, 40, 50 и 45 процентов, а объем продаж - 90, 85, 80 и 83 тыс. штук. При этом ставятся одновременно следующие цели: минимизация затрат на рекламу, завоевание максимальной доли рынка и максимизация объема продаж в течение планируемого периода.