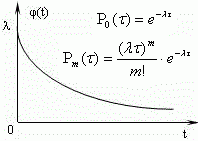Многоканальная СМО с отказами
Рассмотрим многоканальную систему массового обслуживания (всего каналов n), в которую поступают заявки с интенсивностью λ и обслуживаются с интенсивностью μ. Заявка, прибывшая в систему, обслуживается, если хотя бы один канал свободен. Если все каналы заняты, то очередная заявка, поступившая в систему, получает отказ и покидает СМО. Пронумеруем состояния системы по числу занятых каналов:- S0 – все каналы свободны;
- S1 – занят один канал;
- S2 – занято два канала;
- Sk – занято k каналов;
- Sn – все каналы заняты.
На рисунке 6.24 изображен граф состояний, в котором Si – номер канала; λ – интенсивность поступления заявок; μ – соответственно интенсивность обслуживания заявок. Заявки поступают в систему массового обслуживания с постоянной интенсивностью и постепенно занимают один за другим каналы; когда все каналы будут заняты, то очередная заявка, прибывшая в СМО, получит отказ и покинет систему.
Определим интенсивности потоков событий, которые переводят систему из состояния в состояние при движении как слева направо, так и справа налево по графу состояний.
Например, пусть система находится в состоянии S1, т. е. один канал занят, поскольку на его входе стоит заявка. Как только обслуживание заявки закончится, система перейдет в состояние S0.
Например, если заняты два канала, то поток обслуживания, переводящий систему из состояния S2 в состояние S1 будет вдвое интенсивнее: 2-μ; соответственно, если занято k каналов, интенсивность равна k-μ.
Процесс обслуживания является процессом гибели и размножения. Уравнения Колмогорова для этого частного случая будут иметь следующий вид:
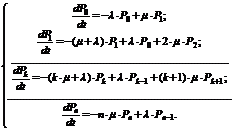(7.25)
Уравнения (7.25) называются уравнениями Эрланга.
Для того, чтобы найти значения вероятностей состояний Р0, Р1, …, Рn, необходимо определить начальные условия:
– Р0(0) = 1, т. е. на входе системы стоит заявка;
– Р1(0) = Р2(0) = … = Рn(0) = 0, т. е. в начальный момент времени система свободна.
Проинтегрировав систему дифференциальных уравнений (7.25), получим значения вероятностей состояний Р0(t), Р1(t), … Рn(t).
Но гораздо больше нас интересуют предельные вероятности состояний. При t → ∞ и по формуле, полученной при рассмотрении процесса гибели и размножения, получим решение системы уравнений (7.25):
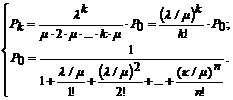(7.26)
В этих формулах отношение интенсивности λ / μ к потоку заявок удобно обозначить ρ. Эту величину называют приведенной интенсивностью потока заявок, то есть среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
С учетом сделанных обозначений система уравнений (7.26) примет следующий вид:
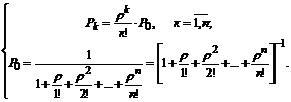(7.27)Зная все вероятности состояний СМО, найдем характеристики эффективности СМО, т. е. абсолютную пропускную способность А, относительную пропускную способность Q и вероятность отказа Ротк.
Заявка, поступившая в систему, получит отказ, если она застанет все каналы занятыми:
.
Вероятность того, что заявка будет принята к обслуживанию:
Q = 1 – Ротк ,
где Q – средняя доля поступивших заявок, обслуживаемых системой, или среднее число заявок обслуженных СМО в единицу времени, отнесенное к среднему числу поступивших за это время заявок:
A=λ·Q=λ·(1-Pотк)
Кроме того, одной из важнейших характеристик СМО с отказами является среднее число занятых каналов. В n-канальной СМО с отказами это число совпадает со средним числом заявок, находящихся в СМО.
Среднее число заявок k можно вычислить непосредственно через вероятности состояний Р0, Р1, … , Рn:
k = 0·P0+1·P1+ ... + n·Pn,
т. е. находим математическое ожидание дискретной случайной величины, которая принимает значение от 0 до n с вероятностями Р0, Р1, …, Рn.
Еще проще выразить величину k через абсолютную пропускную способность СМО, т.е. А. Величина А – среднее число заявок, которые обслуживаются системой в единицу времени. Один занятый канал обслуживает за единицу времени μ заявок, тогда среднее число занятых каналов
