Решение задачи ЛП в неканонической форме симплекс-методом
Пример. Решить следующую задачу ЛП в неканонической форме симплекс-методом:f(x) = x1 – x2 – 3x3 → min (11)
при ограничениях:
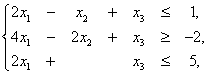 (12)
(12)
x1, x2, x3≥ 0 (13)
Умножая обе части (12) на -1 и прибавляя в левые части системы дополнительные (или слабые) переменные x4 ≥0, x 5 ≥0, x6 ≥0, получим каноническую форму (слабые переменные на целевую функцию не влияют):
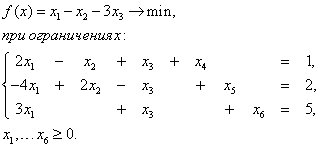 (14)
(14)
Так как все слабые переменные входят со знаком "+", то их можно взять в качестве базисных и составить начальное допустимое базисное решение x0=(0,0,0,1,2,5). В данном случае исключать базисные переменные из целевой функции нет надобности (так как они в ней отсутствуют), поэтому целевую функцию записываем сразу в виде
f(x) = x1 – x2 – 3x3 (15)
(требование симплекс-метода). С помощью начального допустимого базисного решения x0 и выражений (14) и (15) составим начальную симплекс-таблицу (здесь f(x0)=0).
| x1 | x2 | x3 | x4 | x5 | x6 | ||
| f | 0 | -1 | 1 | 3 | 0 | 0 | 0 |
| x4 | 1 | 2 | -1 | 1 | 1 | 0 | 0 |
| x5 | 2 | -4 | 2 | -1 | 0 | 1 | 0 |
| x6 | 5 | 3 | 0 | 1 | 0 | 0 | 1 |
| x1 | x2 | x3 | x4 | x5 | x6 | ||
| f | -46/3 | 0 | 0 | 0 | -19/3 | -11/3 | -1/3 |
| x3 | 4 | 0 | 0 | 1 | 2 | 1 | 0 |
| x2 | 11/3 | 0 | 1 | 0 | -1/3 | 1/3 | 2/3 |
| x1 | 1/3 | 1 | 0 | 0 | -1/2 | -1/3 | 1/3 |
Как видно из последней таблицы, оптимальным решением задачи является x0000=(1/3, 11/3, 4) и f(x0000)=-46/3.
Как итог рассмотрения двух примеров, приведем алгоритм симплекс-метода:
1. привести задачу к канонической форме;
2. привести систему ограничений к диагональной форме и определить базисные переменные;
3. исключить базисные переменные из целевой функции;
4. построить симплекс-таблицу;
5. проверить найденное допустимое базисное решение на оптимальность: если оно оптимально, то решение закончить; если нет, то перейти к пункту 6;
6. вычислить ведущий элемент таблицы;
7. провести симплексное преобразование;
8. построить новое начальное допустимое базисное решение и перейти к пункту 5.
Примечания к симплекс-методу .
1. Если в ведущем столбике нет ни одного строго положительного элемента, то задача не имеет оптимального решения, а целевая функция не ограничена снизу (в задаче на минимум) или не ограничена сверху (в задаче на максимум).
2. Несовместимость системы ограничений (в канонической форме) обнаруживается при построении начального допустимого базисного решения (оно не существует).
3. Если в последней (оптимальной) таблице оценка какой-либо небазисной переменной (число в нулевой строке) равна нулю, то задача имеет бесконечное множество оптимальных решений.
4. Симплекс-метод за конечное число итераций либо приводит к оптимальному решению, либо устанавливает неразрешимость задачи (см. пп. 1,2,3).
5. На каждой итерации симплекс-метод сохраняет допустимость базисного решения, т.е. неотрицательность элементов нулевого столбика - следствие правила выбора ведущей строки.
6. На каждой итерации целевая функция убывает (в задаче на минимум) или возрастаем (в задаче на максимум); это свойство нарушается только в случае зацикливания (см. примечания 11,12).
7. В качестве ведущего столбика можно выбирать любой столбик с положительной оценкой (в задаче на минимум), однако максимальность оценки ведущего столбика ведет к сокращению числа итераций (целевая функция быстро убывает).
8. Слабые переменные со знаком "+" (вводимые для преобразования неравенств вида "≤") можно использовать в качестве базисных переменных, а слабые переменные со знаком "-" (вводимые для преобразования неравенств вида "≥ ") - нет.
9. Структуру симплекс-таблицы можно упростить, если на каждой итерации исключать из таблицы столбцы для базисных переменных. При этом сокращается объем вычислений.
10. При решении симплекс-методом задачи на максимум изменяется только правило выбора ведущей строки (столбик с минимальной отрицательной оценкой) и критерий оптимальности (отсутствие в нулевой строке отрицательных оценок).
11. Допустимое базисное решение, в котором одна или несколько базисных переменных равны нулю, называется вырожденным допустимым базисным решением. Появление такого допустимого базисного решения в процессе решения может привести к зацикливанию, т.е. к повторному вхождению переменной в базис (геометрически: возвращение к предыдущей вершине многогранника). Предвестником зацикливания является неоднозначное определение ведущей строки.
12. Для выхода из зацикливания: в критерии определения ведущей строки вместо элементов 0-го столбика применяют элементы 1-го столбика; если и здесь ведущая строка неоднозначна, то применяют элементы 2-го столбика и т.д., пока ведущая строка не будет определена однозначно.