M-задача
Метод искусственного базиса применяется для решения канонической ЗЛП в случае, когда задача не имеет начального решения с базисом из единичных векторов (ортонормированным базисом).В этом случае в уравнения, не содержащие базисной переменной, добавляют со знаком «+» неотрицательные переменные, называемые искусственными.
В отличие от дополнительных переменных, искусственные переменные влияют на целевую функцию Z(X), они входят в нее с коэффициентами М, причем в задачу на максимум с коэффициентом –М, в задачу на минимум с коэффициентом +М. Величина М предполагается достаточно большим положительным числом (M>>1), значение которого не задается. Поэтому такая задача носит название М-задачи.
В случае решения задачи на максимум расширенная задача имеет вид:
при ограничениях:
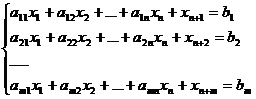
xj≥ 0.
Векторы An+1,An+2,…,An+m называются искусственными векторами. Данная задача имеет начальное опорное решение
Справедлива следующая теорема.
- Если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи;
- если в оптимальном решении М-задачи хотя бы одна искусственная переменная отлична от 0, то исходная задача не имеет решения (из-за несовместимости системы ограничений);
- если М-задача не имеет решения из-за неограниченности целевой функции, то и исходная задача решения не имеет.
Особенности алгоритма метода искусственного базиса
- Виду того, что начальное опорное решение расширенной ЗЛП содержит искусственные переменные, входящие в целевую функцию с коэффициентами -М (max) или +М (min), оценка разложений векторов условий Δj= CбXj -cj состоит из двух слагаемых Δj= Δ’j +Δ’’j( M). Т.к. М – велико, то на первом этапе расчета для нахождения векторов, вводимых в базис, используется только слагаемое Δ’’j( M).
- Векторы, соответствующие искусственным переменным, которые выводятся из базиса опорного решения, исключаются из рассмотрения.
- После того как все векторы, соответствующие искусственным переменным, исключены из базиса, расчет продолжается обычным симплексным методом с использованием оценок Δ’j, не зависящих от М.
- Переход от решения расширенной ЗЛП к решению исходной ЗЛП осуществляется с помощью указанных ранее замечаний.
Пример. Найти решение следующей задачи.
Z(X)=x1+x2+4x3→max
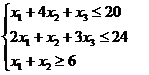 xj≥0 (j=1,2,3)
xj≥0 (j=1,2,3)
Приведем задачу к каноническому виду:
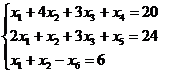
xj ≥ 0 (j=1,2,3,4,5,6)
Z(X)=x1+x2+4x3+0x4+0x5+0x6-Mx7→max
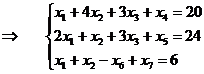
В первых двух уравнениях содержатся базисные переменные x4 и x5 (это дополнительные переменные), а в третьем базисная переменная отсутствует, поэтому введем искусственную переменную x7, которая и будет являться базисной. Решаем М-задачу.
Составим симплексную таблицу:
Базис | Cб | В | 1 | 1 | 4 | 0 | 0 | 0 | -M |
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | |||
| A4
A5
| 0
0 -M | 20
24 6 | 1
2 1 | 4
1 1 | 1
3 0 | 1
0 0 | 0
1 0 | 0
0 -1 | 0
0 1 |
Z0= 0-6М
| -1
-1М↑ | -1
-1 | -4
0 | 0
0 | 0
0 | 0
1 | 0
0 | ||
| A4
←A5 A1 | 0
0 1 | 14
12 6 | 0
0 1 | 3
-1 1 | 1
3 0 | 1
0 0 | 0
1 0 | 1
2 1 | |
| Z1=6 | 0 | 0 | -4↑ | 0 | 0 | -1 | |||
←A4 A3 A1 | 0
4 1 | 10
4 6 | 0
0 1 | 10/3
1/3 1 | 0
1 0 | 1
0 0 | -1/3
1/3 0 | 1/3
2/3 -1 | |
| Z2=22 | 0 | -4/3 | 0 | 0 | 4/3 | 5/3 | |||
| A2
A3 A1 | 1
4 1 | 3
5 3 | 0
0 1 | 1
0 0 | 0
1 0 | 2/10 | 1/10 | 1/10 | |
| Z3=26 | 0 | 0 | 0 | 4/10 | 6/5 | 9/5 | |||
Отбрасывая дополнительные переменные, получим ответ: Zmax=26 при X*=(3,3,5).
Решим прямую задачу линейного программирования симплексным М-методом, с использованием симплексной таблицы. Определим максимальное значение целевой функции F(X) = 2x1+x2+3x3 при следующих условиях-ограничений.
x1+2x2+x3≤1000
3x1+5x2+2x3≤1500
x1≥100
x2≥100
x3≥200
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
1x1 + 2x2 + 1x3 + 1x4 + 0x5 + 0x6 + 0x7 + 0x8 = 1000
3x1 + 5x2 + 2x3 + 0x4 + 1x5 + 0x6 + 0x7 + 0x8 = 1500
1x1 + 0x2 + 0x3 + 0x4 + 0x5-1x6 + 0x7 + 0x8 = 100
0x1 + 1x2 + 0x3 + 0x4 + 0x5 + 0x6-1x7 + 0x8 = 100
0x1 + 0x2 + 1x3 + 0x4 + 0x5 + 0x6 + 0x7-1x8 = 200
Введем искусственные переменные x.
1x1 + 2x2 + 1x3 + 1x4 + 0x5 + 0x6 + 0x7 + 0x8 + 0x9 + 0x10 + 0x11 = 1000
3x1 + 5x2 + 2x3 + 0x4 + 1x5 + 0x6 + 0x7 + 0x8 + 0x9 + 0x10 + 0x11 = 1500
1x1 + 0x2 + 0x3 + 0x4 + 0x5-1x6 + 0x7 + 0x8 + 1x9 + 0x10 + 0x11 = 100
0x1 + 1x2 + 0x3 + 0x4 + 0x5 + 0x6-1x7 + 0x8 + 0x9 + 1x10 + 0x11 = 100
0x1 + 0x2 + 1x3 + 0x4 + 0x5 + 0x6 + 0x7-1x8 + 0x9 + 0x10 + 1x11 = 200
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = 2x1+x2+3x3 - Mx9 - Mx10 - Mx11 => max
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные:
x9 = 100-x1+x6
x10 = 100-x2+x7
x11 = 200-x3+x8
которые подставим в целевую функцию:
F(X) = 2x1 + x2 + 3x3 - M(100-x1+x6) - M(100-x2+x7) - M(200-x3+x8) => max
или
F(X) = (2+1M)x1+(1+1M)x2+(3+1M)x3+(-1M)x6+(-1M)x7+(-1M)x8+(-400M) => max
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
|
1 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
5 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных: x4, x5, x9, x10, x11,
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,0,1000,1500,0,0,0,100,100,200)
План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 |
x11 |
|
0 |
x4 |
1000 | 1 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
x5 | 1500 | 3 | 5 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
x9 | 100 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 0 | 0 | |
x10 | 100 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 | |
|
|
x11 |
200 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
|
Индексная строка |
F(X0) |
-400M |
-2-1M |
-1-1M |
-3-1M |
0 |
0 |
1M |
1M |
1M |
0 |
0 |
0 |
Иногда такую таблицу представляют с дополнительной строкой для М.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
| 0 | x4 | 1000 | 1 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| x5 | 1500 | 3 | 5 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| x9 | 100 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 0 | 0 | |
| x10 | 100 | 0 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 0 | |
| x11 | 200 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | |
| Индексная строка | F(X0) | 0 | -2 | -1 | -3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| M | -400 | -1 | -1 | -1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
Переходим к основному алгоритму симплекс-метода.
|
План |
Базис |
В |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
x11 |
min |
|
1 |
x4 |
1000 |
1 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1000 |
|
|
x5 |
1500 |
3 |
5 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
750 |
|
|
x9 |
100 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
x10 |
100 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
0 |
|
|
x11 |
200 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
200 |
|
Индексная строка |
F(X1) |
-400M |
-2-1M |
-1-1M |
-3-1M |
0 |
0 |
1M |
1M |
1M |
0 |
0 |
0 |
0 |
Посмотреть все итерации
Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план.
Окончательный вариант симплекс-таблицы:
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
| 5 | x4 | 350 | 0 | 0 | 0 | 1 | -0.5 | -0.5 | -0.5 | 0 | 0.5 | 0.5 | 0 |
| x8 | 150 | 0 | 0 | 0 | 0 | 0.5 | 1.5 | 2.5 | 1 | -1.5 | -2.5 | -1 | |
| x1 | 100 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 0 | 0 | |
| x2 | 100 | 0 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 0 | |
| x3 | 350 | 0 | 0 | 1 | 0 | 0.5 | 1.5 | 2.5 | 0 | -1.5 | -2.5 | 0 | |
| Индексная строка | F(X5) | 1350 | 0 | 0 | 0 | 0 | 1.5 | 2.5 | 6.5 | 0 | -2.5+1M | -6.5+1M | 1M |
Оптимальный план можно записать так: x1 = 100, x2 = 100, x3 = 350
F(X) = 2*100 + 1*100 + 3*350 = 1350
