Симплексный метод решения задач линейного программирования
Универсальный метод решения задач ЛП называется симплекс-методом. Применение этого метода и его наиболее часто встречающейся модификации - двухфазного симплекс-метода.При графическом методе решения задач ЛП мы фактически из множества вершин, принадлежащих границе множества решений системы неравенств, выбрали такую вершину, в которой значение целевой функции достигало максимума (минимума). В случае двух переменных этот метод совершенно нагляден и позволяет быстро находить решение задачи.
Если в задаче три и более переменных, а в реальных экономических задачах как раз такая ситуация, трудно представить наглядно область решений системы ограничений. Такие задачи решаются с помощью симплекс-метода или методом последовательных улучшений. Идея метода проста и заключается в следующем.
По определенному правилу находится первоначальный опорный план (некоторая вершина области ограничений). Проверяется, является ли план оптимальным. Если да, то задача решена. Если нет, то переходим к другому улучшенному плану - к другой вершине. значение целевой функции на этом плане (в этой вершине) заведомо лучше, чем в предыдущей. Алгоритм перехода осуществляется с помощью некоторого вычислительного шага, который удобно записывать в виде таблиц, называемых симплекс-таблицами. Так как вершин конечное число, то за конечное число шагов мы приходим к оптимальному решению.
Рассмотрим симплексный метод на конкретном примере задачи о составлении плана.
Еще раз заметим, что симплекс-метод применим для решения канонических задач ЛП, приведенных к специальному виду, т. е. имеющих базис, положительные правые части и целевую функцию, выраженную через небазисные переменные. Если задача не приведена к специальному виду, то нужны дополнительные шаги, о которых мы поговорим позже.
Рассмотрим задачу о плане производства, предварительно построив модель и приведя ее к специальному виду.
Задача.
Для изготовления изделий А и В склад может отпустить сырья не более 80 единиц. Причем на изготовление изделия А расходуется две единицы, а изделия В - одна единица сырья. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если изделий А требуется изготовить не более 50 шт., а изделий В - не более 40 шт. Причем, прибыль от реализации одного изделия А - 5 руб., а от В - 3 руб.
Построим математическую модель, обозначив за х1 количество изделий А в плане, за х2 - количество изделий В. тогда система ограничений будет выглядеть следующим образом:
x1≤50
x2≤40
2x1+x2≤80
x1≥0, x2≥0
5x1+3x2→max
Приведем задачу к каноническому виду, введя дополнительные переменные:
x1+x3=50
x2+x4=40
2x1+x2+x5=80
x1≥0, x2≥0
5x1+3x2→max
-F = -5x1 - 3x2 → min.
Эта задача имеет специальный вид (с базисом, правые части неотрицательны). Ее можно решить симплекс-методом.
I этап. Запись задачи в симплекс-таблицу. Между системой ограничений задачи (3.10) и симплекс-таблицей взаимно-однозначное соответствие. Строчек в таблице столько, сколько равенств в системе ограничений, а столбцов - столько, сколько свободных переменных. Базисные переменные заполняют первый столбец, свободные - верхнюю строку таблицы. Нижняя строка называется индексной, в ней записываются коэффициенты при переменных в целевой функции. В правом нижнем углу первоначально записывается 0, если в функции нет свободного члена; если есть, то записываем его с противоположным знаком. На этом месте (в правом нижнем углу) будет значение целевой функции, которое при переходе от одной таблицы к другой должно увеличиваться по модулю. Итак, нашей системе ограничений соответствует таблица 3.4, и можно переходить ко II этапу решения.
Таблица 3.4
|
базисные |
-х1 |
-х2 |
свободные |
|
х3 х4 х5 |
1 0 2 |
0 1 1 |
50 40 80 |
|
-F |
-5 |
-3 |
0 |
II этап. Проверка опорного плана на оптимальность.
Данной таблице 3.4 соответствует следующий опорный план:
(х1, х2, х3, х4, х5) = (0, 0, 50, 40, 80).
Свободные переменные х1, х2 равны 0; х1 = 0, х2 = 0. А базисные переменные х3, х4, х5 принимают значения х3 = 50, х4 = 40, х5 = 80 - из столбца свободных членов. Значение целевой функции:
-F = - 5х1 - 3х2 = -5 · 0 - 3 · 0 = 0.
Наша задача - проверить, является ли данный опорный план оптимальным. для этого необходимо просмотреть индексную строку - строку целевой функции F.
Возможны различные ситуации.
1. В индексной F-строке нет отрицательных элементов. Значит, план оптимален, можно выписать решение задачи. Целевая функция достигла своего оптимального значения, равного числу, стоящему в правом нижнем углу, взятому с противоположным знаком. Переходим к IV этапу.
2. В индексной строке есть хотя бы один отрицательный элемент, в столбце которого нет положительных. Тогда делаем вывод о том, что целевая функция F→∞ неограниченно убывает.
3. В индексной строке есть отрицательный элемент, в столбце которого есть хотя бы один положительный. Тогда переходим к следующему III этапу. пересчитываем таблицу, улучшая опорный план.
III этап. Улучшение опорного плана.
Из отрицательных элементов индексной F-строки выберем наибольший по модулю, назовем соответствующий ему столбец разрешающим и пометим "↑".
Чтобы выбрать разрешающую строку, необходимо вычислить отношения элементов столбца свободных членов только к положительным элементам разрешающего столбца. Выбрать из полученных отношений минимальное. Соответствующий элемент, на котором достигается минимум, называется разрешающим. Будем выделять его квадратом.
В нашем примере, ![]() , элемент 2 - разрешающий. Строка, соответствующая этому элементу, тоже называется разрешающей (табл. 3.5).
, элемент 2 - разрешающий. Строка, соответствующая этому элементу, тоже называется разрешающей (табл. 3.5).
Таблица 3.5
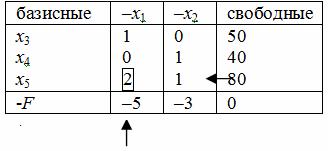
Выбрав разрешающий элемент, делаем перечет таблицы по правилам:
1. В новой таблице таких же размеров, что и ранее, переменные разрешающей строки и столбца меняются местами, что соответствует переходу к новому базису. В нашем примере: х1 входит в базис, вместо х5, которая выходит из базиса и теперь свободная (табл. 3.6).
Таблица 3.6
|
базисные |
-х5 |
-х2 |
свободные |
|
х3 |
-½ | ||
|
х4 |
0 |
|
|
|
х1 |
½ | ½ |
40 |
|
-F |
5/2 |
|
|
2. На месте разрешающего элемента 2 записываем обратное ему число ½.
3. Элементы разрешающей строки делим на разрешающий элемент.
4. Элементы разрешающего столбца делим на разрешающий элемент и записываем с противоположным знаком.
5. Чтобы заполнить оставшиеся элементы таблицы 3.6, осуществляем пересчет по правилу прямоугольника. Пусть мы хотим посчитать элемент, стоящий на месте 50.
Соединяем этот элемент мысленно с разрешающим, находим произведение, вычитаем произведение элементов, находящихся на другой диагонали получившегося прямоугольника. Разность делим на разрешающий элемент.
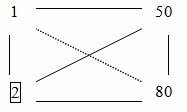
Итак, ![]() . Записываем 10 на место, где было 50. Аналогично:
. Записываем 10 на место, где было 50. Аналогично:
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Таблица 3.7
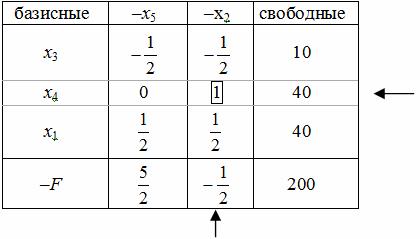
Имеем новую таблицу 3.7, базисными переменными теперь являются переменные {x3,x4,x1}. Значение целевой функции стало равно -200, т.е. уменьшилось. Чтобы проверить данное базисное решение на оптимальность надо перейти опять ко II этапу. Процесс, очевидно, конечен, критерием остановки являются пункт 1 и 2 II этапа.
Доведем решение задачи до конца. Для этого проверим индексную строку и, увидев в ней отрицательный элемент -½, назовем соответствующий ему столбец разрешающим и, согласно III этапу, пересчитаем таблицу. Составив отношения и выбрав среди них минимальное 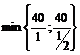 = 40, определили разрешающий элемент 1. теперь пересчет осуществляем согласно правилам 2-5.
= 40, определили разрешающий элемент 1. теперь пересчет осуществляем согласно правилам 2-5.
Таблица 3.8
|
базисные |
-х5 |
-х4 |
свободные |
|
х3 |
-½ | ½ |
30 |
|
х2 |
0 |
1 |
40 |
|
х1 |
½ | -½ |
20 |
|
-F |
5/2 | ½ |
220 |
После пересчета таблицы убеждаемся, что в индексной строке нет отрицательных элементов, следовательно, задача решена, базисный план оптимален.
IVэтап. Выписывание оптимального решения.
Если симплекс-метод остановился согласно пункту 1 II этапа, то решение задачи выписывается следующим образом. Базисные переменные принимают значения столбца свободных членов соответственно. В нашем примере х3 = 30, х2 = 40, х1 = 20. Свободные переменные равны 0, х5 = 0, х4 = 0. Целевая функция принимает значение последнего элемента столбца свободных членов с противоположным знаком: -F = -220 → F= 220, в нашем примере функция исследовалась на min, и первоначально F → max, поэтому фактически знак поменялся дважды. Итак, х* = (20, 40, 30, 0, 0), F* = 220. Ответ к задаче:
- необходимо в план выпуска включить 20 изделий типа А, 40 изделий типа В, при этом прибыль будет максимальной и будет равна 220 руб.
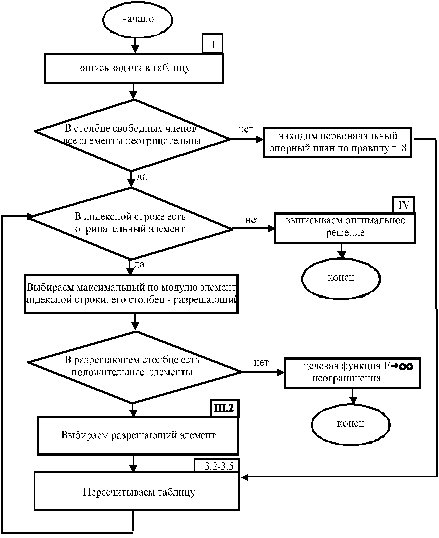
В конце этого параграфа приведем блок-схему алгоритма симплекс-метода, которая в точности повторяет этапы, но, возможно, для некоторых читателей будет более удобна в пользовании, т. к. стрелочки указывают четкую направленность действий.
Ссылки над прямоугольниками в блок-схеме показывают, к какому этапу или подпункту относится соответствующая группа преобразований. правило нахождения первоначального опорного плана будет сформулировано в пункте 3.7.
Пример. Решить следующую задачу ЛП в канонической форме симплекс-методом.
f(x)=x1+9x2+5x3+3x4+4x5+14x6 → min
x1+x4=20
x2+x5=50
x3+x6=30
x4+x5+x6=60
xi ≥ 0, i = 1,…,6
Говорят, что задача ЛП имеет каноническую форму, если все ограничения (кроме условий неотрицательности переменных) имеют вид равенств, а все свободные члены неотрицательны. Так что мы имеем задачу в канонической форме.
Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность.
Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).
Таким образом, идея симплекс-метода основывается на трех свойствах задачи ЛП.
Решение. Чтобы найти начальное допустимое базисное решение, т.е. чтобы определить базисные переменные, систему (5.6) нужно привести к "диагональному" виду. Применяя метод Гаусса (метод последовательного исключения неизвестных), получаем из (5.6):
x2+x1+x3=40
x4+x1=20
x5-x1-x3=10
x6+x3=30
Следовательно, базисными являются переменные x2, x4, x5, x6, им придаем значения, равные
свободным членам соответствующих строк: x2=40, x4=20, x5=10, x6=30,. Переменные x1 и x3 являются небазисными: x1=0, x3=0 .
Построим начальное допустимое базисное решение
x0 = (0,40,0,20,10,30) (5.9)
Для проверки на оптимальность найденного решения x0 нужно из целевой функции исключить базисные переменные (с помощью системы (5.8) ) и построить специальную симплекс таблицу.
После исключения переменных целевую функцию удобно записать в виде:
f(x) = -7x1 – 14x3 +880 (5.10)
Теперь при помощи (5.8) –(5.10) составляем начальную симплекс-таблицу:
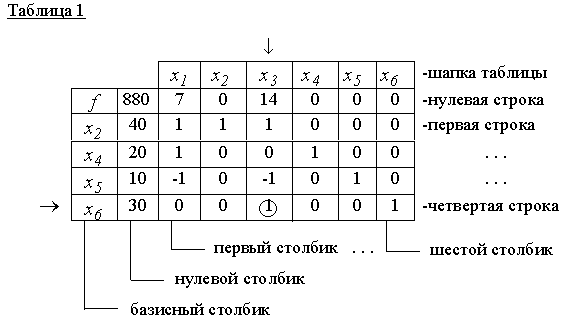
Так что начальное допустимое базисное решение (5.9) неоптимально: 7>0, 14>0.
В нулевом столбике записаны значения базисных переменных. Они обязательно должны быть неотрицательными (см. уравнение (5.7) ). От первой по четвертую строки написаны коэффициенты переменных из системы (5.8).
Так как x0 неоптимально, то надо перейти к другой вершине многогранника допустимых решений (построить новое д.б.р.). Для этого нужно найти ведущий элемент и провести определенное преобразование (симплексное преобразование).
Сначала находим ведущий элемент таблицы, который стоит в пересечении ведущего столбика (столбец с наибольшей положительной оценкой) и ведущей строки (строки, соответствующей минимальному соотношению элементов нулевого столбика к соответствующим элементам (строго положительным) ведущего столбика).
В таблице 1 ведущий столбик - третий столбик, и ведущая строка - четвертая строка (min{40/1,30/1}=30/1) обозначены стрелками, а ведущий элемент - кружочком. Ведущий элемент показывает, что базисную переменную x6 нужно заменить на небазисную x3. Тогда новыми базисными переменными будут x2, x3, x4, x5, , а небазисными -x1, x6, . Это и означает переход к новой вершине многогранника допустимых решений. Чтобы найти значения координат нового допустимого базисного решения x00 нужно строить новую симплекс-таблицу и провести в ней элементарные преобразования:
а) все элементы ведущей строки поделить на ведущий элемент, превратив этим самым ведущий элемент в 1 (для простоты выкладок);
б) с помощью ведущего элемента (равного 1) все элементы ведущего столбика превратить в нули (аналогично методу исключения неизвестных);
В результате в нулевом столбце получены значения новых базисных переменных x2, x3, x4, x5, (см. таблицу 2) - базисные компоненты новой вершины x00 (небазисные компоненты x1=0, x6=0, ).
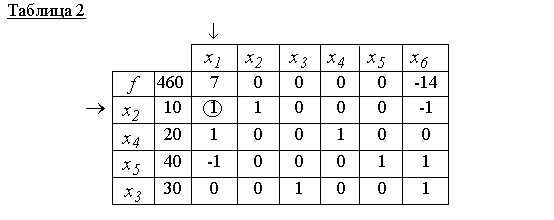
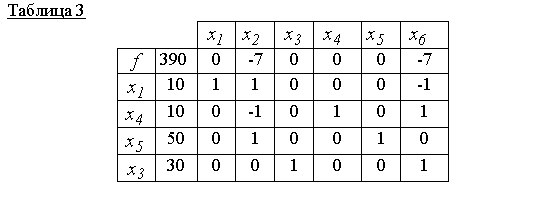
Ответ: x000=(10, 0, 30, 10, 50, 0) - точка минимума, f(x000)=390.
Условно стандартная задача линейного программирования
Необходимо выполнить в указанном порядке следующие задания.- Найти оптимальный план прямой задачи:
а) графическим методом;
б) симплекс-методом (для построения исходного опорного плана рекомендуется использовать метод искусственного базиса). - Построить двойственную задачу.
- Найти оптимальный план двойственной задачи из графического решения прямой, используя условия дополняющей нежесткости.
- Найти оптимальный план двойственной задачи по первой теореме двойственности, используя окончательную симплекс-таблицу, полученную при решении прямой задачи (см. п. 1б). Проверить утверждение «значения целевых функций пары двойственных задач на своих оптимальных решениях совпадают».
- Двойственную задачу решить симплекс-методом, затем, используя окончательную симплекс-таблицу двойственной задачи найти оптимальный план прямой задачи по первой теореме двойственности. Сравнить результат с результатом, который был получен графическим методом (см. п. 1а).
- Найти оптимальное целочисленное решение:
а) графическим методом;
б) Методом Гомори.
Сравнить значения функций целочисленного и нецелочисленного решений
Вопросы для самоконтроля
- Как строится симплекс-таблица?
- Как отражается смена базиса в таблице?
- Сформулируйте критерий остановки симплекс-метода.
- Как организовать пересчет таблицы?
- С какой строки удобно начинать пересчет таблицы?