Игры с природой. Пример решения задачи
Фирма производит платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение апреля-мая на единицу продукции составят: платья – 5 ден. ед., костюмы – 25 ден. ед. Цена реализации составит 10 ден. ед. и 40 ден. ед. соответственно. По данным наблюдений за несколько предыдущих лет фирма может реализовать в условиях теплой погоды 1 220 платьев и 550 костюмов, при прохладной погоде – 410 платьев и 930 костюмов. В связи с возможными изменениями погоды определить стратегию фирмы в выпуске продукции, обеспечивающую ей максимальный доход. Задачу решить графическим методом и с использованием критерия Гурвица, приняв степень оптимизма 0,4.Решение. У фирмы две стратегии: A1: выпустить продукцию, считая, что погода будет теплой; A2: выпустить продукцию, считая, что погода будет прохладной.
У природы две стратегии: B1: погода теплая; B2: погода прохладная.
Найдем элементы платежной матрицы:
1) a11 – доход фирмы при выборе стратегии A1 при условии B1:
a11 = (10-5)*1220+(40-25)*550 = 14350
2) a12 – доход фирмы при выборе A1 при условии B2. Фирма выпустит 1220 платьев, а продаст 410, доход от реализации платьев
a12 = (10-5)*410-5*(1220-410)+(40-25)*550=6250
3) аналогично при стратегии A2 в условиях B1 фирма выпустит 930 костюмов, а продаст 550;
a21 = (10-5)*410+(40-25)*550-25*(930-550)=800
4) a22 = (10-5)*410+(40-25)*930=16000
Платежная матрица:
Далее решаем через калькулятор. Рассмотрим игру двух лиц, интересы которых противоположны. Такие игры называют антагонистическими играми двух лиц. В этом случае выигрыш одного игрока равен проигрышу второго, и можно описать только одного из игроков.
Чистой стратегией игрока I (производитель) является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II (природа
) является выбор одного из столбцов этой же матрицы.
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
| Игроки | B1 | B2 | a = min(Ai) |
| A1 | 14350 | 6250 | 6250 |
| A2 | 800 | 16000 | 800 |
| b = max(Bi) | 14350 | 16000 |
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 6250, которая указывает на максимальную чистую стратегию A1.
Верхняя цена игры b = min(bj) = 14350.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 6250 ≤ y ≤ 14350. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).
Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.
Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I.
3. Находим решение игры в смешанных стратегиях.
Решим задачу геометрическим методом, который включает в себя следующие этапы:
1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A1, правый - стратегии A2 (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S1 = (p1,p2).
2. На левой оси ординат откладываются выигрыши стратегии A1. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A2.
Решение игры (2xn) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.
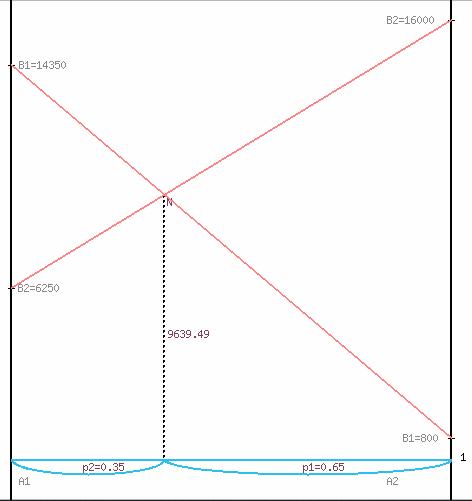
y = 14350 + (800 - 14350)p2
y = 6250 + (16000 - 6250)p2
Откуда
p1 = 152/233 = 0,652
p2 = 81/233 = 0,348
Цена игры, y = 2246000/233
Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений
14350q1+6250q2 = y
800q1+16000q2 = y
q1+q2 = 1
или
14350q1+6250q2 = 9639113/233
800q1+16000q2 = 9639113/233
q1+q2 = 1
Решая эту систему, находим:
q1 = 195/466.
q2 = 271/466.
Ответ:
Цена игры: y = 2246000/233 = 9639.49, векторы стратегии игроков:
Q(195/466, 271/466), P(152/233, 81/233)
Таким образом, если придерживаться стратегии на 65%, что погода будет теплой, это обеспечит максимальный доход в размере 9640 ден.ед. Оптимальный план производства швейных изделий составит: 0.652 (1 220; 550) + 0.348 (410; 930) = (938.4; 682.1). Таким образом, фирме целесообразно производить в течение апреля-мая 938 платьев и 682 костюма, тогда при любой погоде она получит доход не менее 9 639.485 ден.ед.
4. Проверим правильность решения игры с помощью критерия оптимальности стратегии.
∑aijqj ≤ v
∑aijpi ≥ v
M(P1;Q) = (14350•195/466) + (6250•271/466) = 9639.485 = v
M(P2;Q) = (800•195/466) + (16000•271/466) = 9639.485 = v
M(P;Q1) = (14350•152/233) + (800•81/233) = 9639.485 = v
M(P;Q2) = (6250•152/233) + (16000•81/233) = 9639.485 = v
Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно.
В условиях неопределённости, если не представляется возможным фирме использовать смешанную стратегию (договоры с другими организациями), для определения оптимальной стратегии фирмы используем критерии природы и платежную матрицу (1).
Критерий Гурвица является критерием пессимизма - оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение:
max(si), где si = y min(aij) + (1-y)max(aij)
Рассчитываем si.
s1 = 0.4•6250+(1-0.4)•14350 = 11110
s2 = 0.4•800+(1-0.4)•16000 = 9920
| Ai | П1 | П2 | min(aij) | max(aij) | y min(aij) + (1-y)max(aij) |
| A1 | 14350 | 6250 | 6250 | 14350 | 11110 |
| A2 | 800 | 16000 | 800 | 16000 | 9920 |
Выбираем из (11110; 9920) максимальный элемент max=11110
Вывод: выбираем стратегию N=1.
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A1 (выпустить продукцию, считая, что погода будет теплой).
см. также решение задачи про запасы сырья.