Распределение Пуассона
При рассмотрении маловероятных событий, имеющих место в большой серии независимых испытаний некоторое (конечное) число раз, вероятности появления этих событий подчиняются закону Пуассона или закону редких событий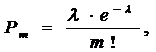 , где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828, m -частота данного события, математическое ожидание M[X] равно λ.
, где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828, m -частота данного события, математическое ожидание M[X] равно λ.
Ряд распределения закона Пуассона имеет вид:
| X | 0 | 1 | 2 | … | m | … |
| P | e-λ | λe-λ | … | … |
Числовые характеристики случайной величины Х
Математическое ожидание распределения ПуассонаM[X] = λ
Дисперсия распределения Пуассона
D[X] = λ
Закон Пуассона можно применять для совокупностей, достаточно больших по объему (n > 100) и имеющих достаточно малую долю единиц, обладающих данным признаком (p < 0,1).
При этом распределение Пуассона можно применить, когда на только не известно значение n – общего числа возможных результатов, но и когда не известно конечное число, которое n может представлять. Там, где есть среднее число случаев наступления события, вероятность наступления события описывается членами разложения:
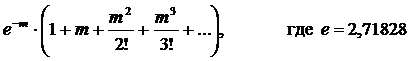
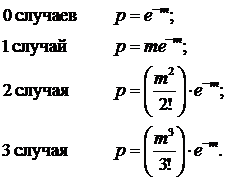
Поэтому, если среднее число землетрясений равно одному в месяц, то m=1 и вероятность случаев в месяц будет следующей, рассчитанной по приблизительному значению e-m=0,3679:
| Число случаев | Вероятность | Приблизительный числовой эквивалент |
| 0 | e-m | 0,3679 |
| 1 | me-m | 0,3679 |
| 2 | e-m | 0,1839 |
| 3 | e-m | 0,0613 |
Пример. В результате проверки 1000 партий одинаковых изделий получено следующее распределение количества бракованных изделий в партии:
| Количество брака, m1 | 0 | 1 | 2 | 3 | 4 | Итого |
| Количество партий, содержащих данное число бракованных изделий, fi | 604 | 306 | 77 | 12 | 1 | 1000 |
Определим среднее число бракованных изделий в партии:
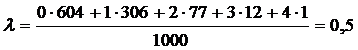
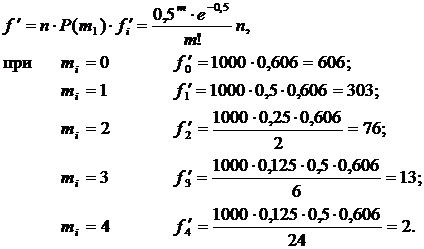
| 604 | 306 | 77 | 12 | 1 |
| 606 | 303 | 76 | 13 | 2 |
Сопоставление свидетельствует о соответствии эмпирического распределения распределению Пуассона.
Перейти к онлайн решению своей задачи
Пример №2. Отдел технического контроля проверил n партий однотипных изделий и установил, что число Х нестандартных изделий в одной партии имеет эмпирическое распределение, приведенное в таблице, в одной строке которой указано количество xi нестандартных изделий в одной партии, а в другой строке – количество ni партий, содержащих xi нестандартных изделий. Требуется при уровне значимости α=0.05 проверить гипотезу о том, что случайная величина Х (число нестандартных изделий в одной партии) распределена по закону Пуассона.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 370 | 360 | 190 | 63 | 14 | 3 |
Проверим гипотезу о том, что Х распределено по закону Пуассона с помощью сервиса
проверка статистических гипотез.
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону; λ = xср.
i = 0: p0 = 0.3679, np0 = 367.88
i = 1: p1 = 0.3679, np1 = 367.88
i = 2: p2 = 0.1839, np2 = 183.94
i = 3: p3 = 0.0613, np3 = 61.31
i = 4: p4 = 0.0153, np4 = 15.33
i = 5: p5 = 0.0031, np5 = 3.07
i = 6: 17=14 + 3
i = 6: 18.39=15.33 + 3.07
| i | Наблюдаемая частота ni | pi | Ожидаемая частота npi | Слагаемые статистики Пирсона Ki |
| 0 | 370 | 0.37 | 367.88 | 0.0122 |
| 1 | 360 | 0.37 | 367.88 | 0.17 |
| 2 | 190 | 0.18 | 183.94 | 0.2 |
| 3 | 63 | 0.0613 | 61.31 | 0.0464 |
| 4 | 17 | 0.0153 | 18.39 | 0.11 |
| 1000 | 0.53 |
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям s, k (число интервалов), r=1 (параметр λ).
Kkp = 11.14329; Kнабл = 0.53
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют распределение Пуассона.
Перейти к онлайн решению своей задачи
Пример. В цехе с 10 станками ежедневно регистрировалось число вышедших из строя станков. Всего было проведено 200 наблюдений, результаты которых приведены ниже.
Необходимо:
- Определить исследуемый признак и его тип (дискретный или непрерывный).
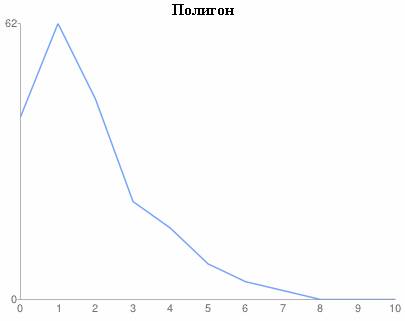
- В зависимости от типа признака построить полигон или гистограмму относительных частот.
- На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
- Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.
- Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,99.
- При уровне значимости 0,05 проверить гипотезу о том, что число выбывших из строя станков имеет распределение Пуассона.
Решение. Задан дискретный признак. Строим таблицу для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)·f | (x-x)2·f | (x-x)3·f | Частота, fi/n |
| 0 | 41 | 0 | 41 | 73.8 | 132.84 | -239.11 | 0.21 |
| 1 | 62 | 62 | 103 | 49.6 | 39.68 | -31.74 | 0.31 |
| 2 | 45 | 90 | 148 | 9 | 1.8 | 0.36 | 0.23 |
| 3 | 22 | 66 | 170 | 26.4 | 31.68 | 38.02 | 0.11 |
| 4 | 16 | 64 | 186 | 35.2 | 77.44 | 170.37 | 0.08 |
| 5 | 8 | 40 | 194 | 25.6 | 81.92 | 262.14 | 0.04 |
| 6 | 4 | 24 | 198 | 16.8 | 70.56 | 296.35 | 0.02 |
| 7 | 2 | 14 | 200 | 10.4 | 54.08 | 281.22 | 0.01 |
| 8 | 0 | 0 | 200 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 200 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 200 | 0 | 0 | 0 | 0 |
| 200 | 360 | 246.8 | 490 | 777.6 | 1 |
Находим показатели центра распределения.
Средняя взвешенная
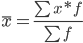
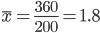
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 10 - 0 = 10
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
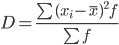
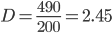
Несмещенная оценка дисперсии - состоятельная оценка дисперсии.
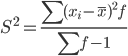
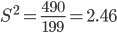
Среднее квадратическое отклонение.
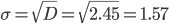
Каждое значение ряда отличается от среднего значения 1.8 не более, чем на 1.57
Оценка среднеквадратического отклонения.
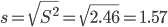
Доверительный интервал для генерального среднего.
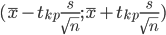
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа.
В этом случае 2Ф(tkp) = 1 - γ
Ф(tkp) = (1 - γ)/2 = 0.99/2 = 0.495
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.495
tkp(γ) = (0.495) = 2.58
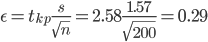
(1.8 - 0.29;1.8 + 0.29) = (1.51;2.09)
С вероятностью 0.99 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна P(χ2n-1 < hH) = (1-γ)/2 = 0.005. Для количества степеней свободы k = 199, по таблице распределения хи-квадрат находим:
χ2(199;0.005) = 255.2642.
Случайная ошибка дисперсии:
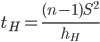
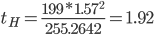
Вероятность выхода за верхнюю границу равна P(χ2n-1 ≥ hB) = 1 - P(χ2n-1 < hH) = 1 - 0.005 = 0.995. Для количества степеней свободы k = 199, по таблице распределения хи-квадрат находим:
χ2(199;0.995) = 152.241.
Случайная ошибка дисперсии:
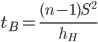
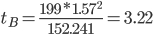
(2.46 - 1.92; 2.46 + 3.22)
(0.54; 5.68)
Найдем верхнюю границу доверительного интервала для среднеквадратического отклонения с надежностью γ = 0.99.
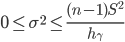
P(χ2n-1 > hγ) = 0.99. Для количества степеней свободы k = 199, по таблице распределения хи-квадрат находим:
χ2(199;0.99) = 156.432.
Случайная ошибка дисперсии:
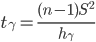
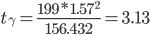
0 ≤ σ2 ≤ 3.13
Проверка гипотез о виде распределения.
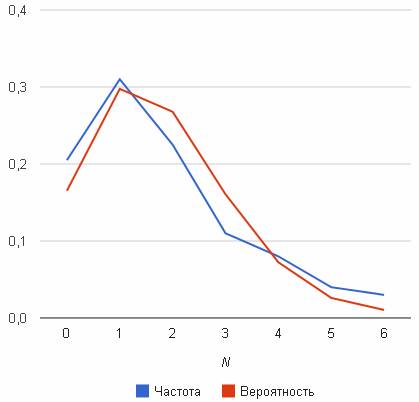
2. Проверим гипотезу о том, что Х распределено по закону Пуассона.
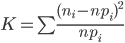
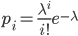
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону.
Примем в качестве оценки параметра λ распределения Пуассона выборочную среднюю xср = 1.8. Следовательно, предполагаемый закон Пуассона имеет вид:
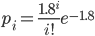
i = 0: p0 = 0.17, np0 = 33.06
i = 1: p1 = 0.3, np1 = 59.51
i = 2: p2 = 0.27, np2 = 53.56
i = 3: p3 = 0.16, np3 = 32.13
i = 4: p4 = 0.0723, np4 = 14.46
i = 5: p5 = 0.026, np5 = 5.21
i = 6: p6 = 0.00781, np6 = 1.56
i = 7: p7 = 0.00201, np7 = 0.4
i = 8: p8 = 0.000452, np8 = 0.0904
i = 9: p9 = 9.0E-5, np9 = 0.0181
i = 10: p10 = 1.6E-5, np10 = 0.00325
Объединим малочисленные частоты: (10,9,8,7,6) и соответствующие им теоретические частоты.
| i | Наблюдаемая частота ni | pi | Ожидаемая частота npi | Слагаемые статистики Пирсона Ki |
| 0 | 41 | 0.17 | 33.06 | 1.91 |
| 1 | 62 | 0.3 | 59.51 | 0.1 |
| 2 | 45 | 0.27 | 53.56 | 1.37 |
| 3 | 22 | 0.16 | 32.13 | 3.2 |
| 4 | 16 | 0.0723 | 14.46 | 0.16 |
| 5 | 8 | 0.026 | 5.21 | 1.5 |
| 6 | 6 | 0.0104 | 2.07 | 7.42 |
| 200 | 15.66 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям s, k (число интервалов), r=1 (параметр λ).
Kkp(0.05;5) = 11.07050; Kнабл = 15.66
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по закону Пуассона.