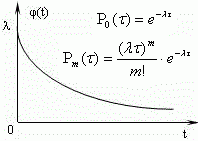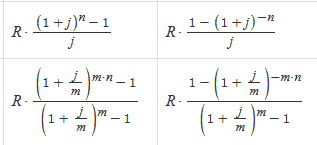Элементы теории массового обслуживания
Основные понятия систем массового обслуживания
Системы массового обслуживания (МО) являются частью более широкого класса динамических систем, которые иногда называют системами потоков. Системой потоков называется система, в которой некоторые предметы перемещаются по одному или нескольким каналам с ограниченной пропускной способностью с целью перемещения из одной точки в другую.При анализе систем потоков их разбивают на два основных класса:
- регулярные системы, т. е. системы, в которых потоки ведут себя предсказуемым образом (известны величина потока и время его появления в канале). В случае, когда канал один, расчет системы тривиален. Очевидно, что между интенсивностью потока R и скоростью обслуживания с есть соотношение R < c;
- нерегулярные системы, т. е. системы, в которых потоки ведут себя непредсказуемым образом.
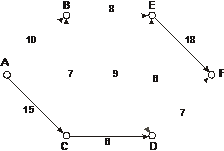
Рис. 1
Имеется семь дорог. Необходимо перевезти груз из А в Д. Пропускная способность каждого канала известна. Какова пропускная способность сети и каким путем должен следовать поток? Решить эту задачу можно с помощью теоремы о максимальном потоке, которую мы рассматривали ранее (рис. 7.20).
Ко второму классу относятся случайные вероятные потоки, в которых время поступления требования не определено, число требований непредсказуемо. Решением таких задач и занимается теория массового обслуживания.
В общем случае система массового обслуживания может быть представлена на рис. 2.
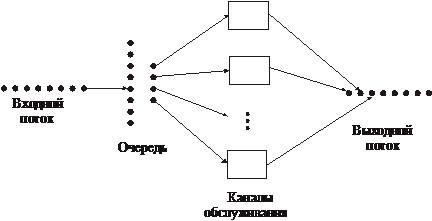
Предметом теории массового обслуживания является установление зависимости между характером потока заявок, числом каналов, производительностью, правильностью работы и эффективностью.
В качестве характеристик эффективности могут применяться следующие величины и функции:
- среднее количество заявок, которые может обслужить СМО в единицу времени;
- среднее количество заявок, получающих отказ и покидающих СМО;
- вероятность того, что поступившая заявка немедленно будет обслужена;
- среднее время ожидания в очереди;
- среднее количество заявок в очереди;
- средний доход СМО в единицу времени и другие экономические показатели СМО.
Марковский процесс требует, чтобы все потоки были пуассоновскими (без последействий), но аппарат марковских процессов используется и тогда, когда процесс отличен от марковского. В этом случае характеристики СМО могут быть оценены приблизительно: чем сложнее СМО, тем точнее приближение.
Марковский случайный процесс с дискретными состояниями и непрерывным временем имеет место в системах массового обслуживания.
Системы массового обслуживания - это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания.
С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если такое имеется в блоке ожидания, цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работыобслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.
Примерами систем массового обслуживания могут служить:
• посты технического обслуживания автомобилей;
• посты ремонта автомобилей;
• персональные компьютеры, обслуживающие поступающие заявки или требования на решение тех или иных задач;
• станции технического обслуживания автомобилей;
• аудиторские фирмы;
• отделы налоговых инспекций, занимающиеся приемкой и проверкой текущей отчетности предприятий;
• телефонные станции и т. д.
Основными компонентами системы массового обслуживания любого вида являются:
• входной поток поступающих требований или заявок на обслуживание;
• дисциплина очереди;
• механизм обслуживания.
Раскроем содержание каждого из указанных выше компонентов.
Для описания входного потока требованийнужно задать вероятностный закон, определяющий последовательность моментов поступления требований на обслуживание и указать количество таких требований в каждом очередном поступлении. При этом, как правило, оперируют понятием «вероятностное распределение моментов поступления требований». Здесь могут поступать как единичные, так и групповые требования (требования поступают группами в систему). В последнем случае обычно речь идет о системе обслуживания с параллельно-групповым обслуживанием.
Дисциплина очереди —это важный компонент системы массового обслуживания, он определяет принцип, в соответствии с которым поступающие на вход обслуживающей системы требования подключаются из очереди к процедуре обслуживания. Чаще всего используются дисциплины очереди, определяемые следующими правилами:
• первым пришел — первым обслуживаешься;
• пришел последним - обслуживаешься первым;
• случайный отбор заявок;
• отбор заявок по критерию приоритетности;
• ограничение времени ожидания момента наступления обслуживания (имеет место очередь с ограниченным временем ожидания обслуживания, что ассоциируется с понятием «допустимая длина очереди»).
Механизм обслуживанияопределяется характеристиками самой процедуры обслуживания и структурой обслуживающей системы. К характеристикам процедуры обслуживания относятся: продолжительность процедуры обслуживания и количество требований, удовлетворяемых в результате выполнения каждой такой процедуры. Для аналитического описания характеристик процедуры обслуживания оперируют понятием «вероятностное распределение времени обслуживания требований».
Следует отметить, что время обслуживания заявки зависит от характера самой заявки или требований клиента и от состояния и возможностей обслуживающей системы. В ряде случаев приходится также учитывать вероятность выхода обслуживающего прибора по истечении некоторого ограниченного интервала времени.
Структура обслуживающей системы определяется количеством и взаимным расположением каналов обслуживания (механизмов, приборов и т. п.). Прежде всего следует подчеркнуть, что система обслуживания может иметь не один канал обслуживания, а несколько; система такого рода способна обслуживать одновременно несколько требований. В этом случае все каналы обслуживания предлагают одни и те же услуги, и, следовательно, можно утверждать, что имеет место параллельное обслуживание.
Система обслуживания может состоять из нескольких разнотипных каналов обслуживания, через которые должно пройти каждое обслуживаемое требование, т. е. в обслуживающей системе процедуры обслуживания требований реализуются последовательно. Механизм обслуживания определяет характеристики выходящего (обслуженного) потока требований.
Рассмотрев основные компоненты систем обслуживания, можно констатировать, что функциональные возможности любой системы массового обслуживания определяются следующими основными факторами:
• вероятностным распределением моментов поступлений заявок на обслуживание (единичных или групповых);
• вероятностным распределением времени продолжительности обслуживания;
• конфигурацией обслуживающей системы (параллельное, последовательное или параллельно-последовательное обслуживание);
• количеством и производительностью обслуживающих каналов; ]
• дисциплиной очереди;
• мощностью источника требований.
В качестве основных критериев эффективности функционирования систем массового обслуживания в зависимости от характера решаемой задачи могут выступать:
• вероятность немедленного обслуживания поступившей заявки;
• вероятность отказа в обслуживании поступившей заявки;
• относительная и абсолютная пропускная способность системы;
• средний процент заявок, получивших отказ в обслуживании;
• среднее время ожидания в очереди;
• средняя длина очереди;
• средний доход от функционирования системы в единицу времени и т. п.
Предметом теории массового обслуживанияявляется установление зависимости между факторами, определяющими функциональные возможности системы массового обслуживания, и эффективностью ее функционирования. В большинстве случаев все параметры, описывающие системы массового обслуживания, являются случайными величинами или функциями, поэтому эти системы относятся к стохастическим системам.
Случайный характер потока заявок (требований), а также, в общем случае, и длительности обслуживания приводит к тому, что в системе массового обслуживания происходит случайный процесс. По характеру случайного процесса, происходящего в системе массового обслуживания (СМО), различают системы марковские и немарковские. В марковских системахвходящий поток требований и выходящий поток обслуженных требований (заявок) являются пуассоновскими. Пуассоновские потоки позволяют легко описать и построить математическую модель системы массового обслуживания. Данные модели имеют достаточно простые решения, поэтому большинство известных приложений теории массового обслуживания используют марковскую схему. В случае немарковских процессовзадачи исследования систем массового обслуживания значительно усложняются и требуют применения статистического моделирования, численных методов с использованием ЭВМ.
Независимо от характера процесса, протекающего в системе массового обслуживания, различают два основных вида СМО:
• системы с отказами, в которых заявка, поступившая в систему в момент, когда все каналы заняты, получает отказ и сразу же покидает очередь;
• системы с ожиданием (очередью), в которых заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь и ждет, пока не освободится один из каналов.
Системы массового обслуживания с ожиданием делятся на системы с ограниченным ожиданием и системы с неограниченным ожиданием.
В системах с ограниченным ожиданиемможет ограничиваться:
• длина очереди;
• время пребывания в очереди.
В системах с неограниченным ожиданиемзаявка, стоящая в очереди, ждет обслуживания неограниченно долго, т.е. пока не подойдет очередь.
Все системы массового обслуживания различают по числу каналов обслуживания:
• одноканальные системы;
• многоканальные системы.
Приведенная классификация СМО является условной. На практике чаще всего системы массового обслуживания выступают в качестве смешанных систем. Например, заявки ожидают начала обслуживания до определенного момента, после чего система начинает работать как система с отказами.