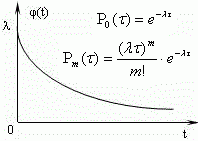Элементы теории массового обслуживания
Теория СМО посвящена разработке методов анализа, проектирования и рациональной организации систем, относящихся к различным областям деятельности, таким как связь, вычислительная техника, торговля, транспорт, военное дело. Несмотря на все свое разнообразие, приведенные системы обладают рядом типичных свойств, а именно.- СМО (системы массового обслуживания) - это модели систем, в которые в случайные моменты времени извне или изнутри поступают заявки (требования). Они должны тем или иным образом быть обслужены системой. Длительность обслуживания чаще всего случайна.
- СМО представляет собой совокупность обслуживающего оборудования и персонала при соответствующей организации процесса обслуживания.
- Задать СМО – это значит задать ее структуру и статистические характеристики последовательности поступления заявок и последовательности их обслуживания.
- показатели, характеризующие систему в целом: число n занятых каналов обслуживания, число обслуженных (λb), ожидающих обслуживание или получивших отказ заявок (λc) в единицу времени и т.д.;
- вероятностные характеристики: вероятность того, что заявка будет обслужена (Pобс) или получит отказ в обслуживании (Pотк), что все приборы свободны (p0) или определенное число их занято (pk), вероятность наличия очереди и т.д.;
- экономические показатели: стоимость потерь, связанных с уходом не обслуженной по тем или иным причинам заявки из системы, экономический эффект, полученный в результате обслуживания заявки, и т.д.
В ходе выполнения домашней контрольной работы изучаются простейшие СМО. Это системы разомкнутого типа, бесконечный источник заявок в систему не входит. Входной поток заявок, потоки обслуживания и ожидания этих систем являются простейшими. Приоритеты отсутствуют. Системы однофазные.
Многоканальная система с отказами
Система состоит из одного узла обслуживания, содержащего n каналов обслуживания, каждый из которых может обслуживать только одну заявку.Все каналы обслуживания одинаковой производительности и для модели системы неразличимы. Если заявка поступила в систему и застала хотя бы один канал свободным, она мгновенно начинает обслуживаться. Если в момент поступления заявки в систему все каналы заняты, то заявка покидает систему не обслуженной.
Смешанные системы
- Система с ограничением на длину очереди.
Состоит из накопителя (очереди) и узла обслуживания. Заявка покидает очередь и уходит из системы, если в накопителе к моменту ее появления уже находятся m заявок (m – максимально возможноечисло мест в очереди). Если заявка поступила в систему и застала, хотя бы один канал свободным, она мгновенно начинает обслуживаться. Если в момент поступления заявки в систему все каналы заняты, то заявка не покидает систему, а занимает место в очереди. Заявка покидает систему не обслуженной, если к моменту её поступления в систему заняты все каналы обслуживания и все места в очереди.
Для каждой системы определяется дисциплина очереди. Это система правил, определяющих порядок поступления заявок из очереди в узел обслуживания. Если все заявки и каналы обслуживания равнозначны, то чаще всего действует правило «кто раньше пришел, тот раньше обслуживается». - Система с ограничением на длительность пребывания заявки в очереди.
Состоит из накопителя (очереди) и узла обслуживания. От предыдущей системы она отличается тем, что заявка, поступившая в накопитель (очередь), может ожидать начала обслуживания лишь ограниченное время Тож (чаще всего это случайная величина). Если её время Тож истекло, то заявка покидает очередь и уходит из системы не обслуженной.
Математическое описание СМО
СМО рассматриваются как некоторые физические системы с дискретными состояниями х0, х1, …, хn, функционирующие при непрерывном времени t. Число состояний n может быть конечным или счетным (n → ∞). Система может переходить из одного состояния хi (i=1, 2, … ,n) в другое хj (j=0, 1, … ,n) в произвольный момент времени t. Чтобы показать правила таких переходов, используют схему, называемую графом состояний. Для типов перечисленных выше систем графы состояний образуют цепь, в которой каждое состояние (кроме крайних) связано прямой и обратной связью с двумя соседними состояниями. Это схема гибели и размножения.Переходы из состояния в состояние происходят в случайные моменты времени. Удобно считать, что эти переходы происходят в результате действия каких-то потоков (потоков входных заявок, отказов в обслуживании заявок, потока восстановления приборов и т.д.). Если все потоки простейшие, то протекающий в системе случайный процесс с дискретным состоянием и непрерывным временем будет марковским.
Поток событий - это последовательность однотипных событий, протекающих в случайные моменты времени. Его можно рассматривать как последовательность случайных моментов времени t1, t2, … появления событий.
Простейшим называют поток, обладающий следующими свойствами:
- Ординарность. События следуют по одиночке (противоположность потоку, где события следуют группами).
- Стационарность. Вероятность попадания заданного числа событий на интервал времени Т зависит только от длины интервала и не зависит от того, где на оси времени находиться этот интервал.
- Отсутствие последействия. Для двух непересекающихся интервалов времени τ1 и τ2 число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой интервал.
Марковские случайные события описываются обыкновенными дифференциальными уравнениями. Переменными в них служат вероятности состояний р0(t), p1(t),…,pn(t).
Для очень больших моментов времени функционирования систем (теоретически при t → ∞) в простейших системах (системы, все потоки в которых – простейшие, а граф – схема гибели и размножения) наблюдается установившийся,или стационарныйрежим работы. В этом режиме система будет изменять свое состояние, но вероятности этих состояний (финальные вероятности) рк, к= 1, 2 ,…, n, не зависят от времени и могут рассматриваться как среднее относительное время пребывания системы в соответствующем состоянии.
Содержание
- Уравнения Колмогорова
- Марковские процессы, Марковская цепь
- Система массового обслуживания (Классификация систем массового обслуживания)
- Элементы теории массового обслуживания: Относительная пропускная способность, Абсолютная пропускная способность СМО
- СМО с ожиданием (очередью), Многоканальная СМО с ожиданиями, СМО с отказами
- Модель обслуживания машинного парка
Одноканальные СМО
- Одноканальная модель с пуассоновским входным потоком с экспоненциальным распределением длительности обслуживания
- Одноканальная СМО с ожиданием
- Одноканальная СМО с отказами
Многоканальные СМО
- Многоканальная модель с пуассоновским входным потоком и экспоненциальным распределением длительности обслуживания
- Многоканальная СМО с отказами
- Системы с ожиданием при неограниченном входящем потоке