Показательное уравнение регрессии
Показательное уравнение регрессии имеет видy = a bx (для временного ряда выражение y = a bt носит название показательного тренда). Для расчетов уравнение приводят к виду: ln(y)=ln(a)+x·ln(b)
Точечный коэффициент эластичности:
Э(x0)=x0 ln(b).
Средний коэффициент эластичности: Эx=x·ln(b)
В случае b = e (примерное значение экспоненты e ≈ 2.718281828), показательное уравнение регрессии называется экспоненциальным и записывается как y=a·ex.
Здесь b - темп изменения в разах или константа тренда, которая показывает тенденцию ускоренного и все более ускоряющегося возрастания уровней.
Пример. Необходимо изучить зависимость потребительским расходами на моторное масло (у) и располагаемым личным доходом (х).
| Годы | Личный располагаемый доход | Расходы на моторное масло |
| 1963 | 622,9 | 4,9 |
| 1964 | 658 | 5,2 |
| 1965 | 700,4 | 5,5 |
| 1966 | 740,6 | 5,6 |
| 1967 | 774,4 | 5,6 |
| 1968 | 816,2 | 5,3 |
| 1969 | 853,5 | 5 |
| 1970 | 876,8 | 4,7 |
| 1971 | 900 | 4,6 |
| 1972 | 951,4 | 5 |
| 1973 | 1007,9 | 5,4 |
| 1974 | 1004,8 | 4,2 |
| 1975 | 1010,8 | 4,2 |
| 1976 | 1056,2 | 4,6 |
| 1977 | 1105,4 | 4,4 |
| 1978 | 1162,3 | 4,7 |
| 1979 | 1200,7 | 4,7 |
| 1980 | 1209,5 | 3,9 |
| 1981 | 1248,6 | 3,6 |
| 1982 | 1254,4 | 3,6 |
| 1983 | 1284,6 | 4 |
Перейти к онлайн решению своей задачи
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
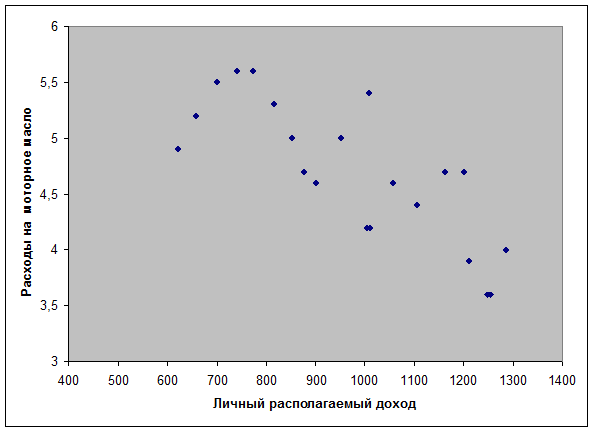
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит экспоненциальный характер.
Показательное уравнение регрессии имеет вид y = a bx + ε
Составляем систему нормальных уравнений с помощью онлайн-калькулятора Нелинейная регрессия
.
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для наших данных система уравнений имеет вид
21a + 20439.4 b = 32.32
20439.4 a + 20761197.38 b = 31007.03
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = -0.000515, a = 2.04
Уравнение регрессии (эмпирическое уравнение регрессии):
y = e2.04*e-0.000515x = 7.69529*0.99948x
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| x | log(y) | x2 | log(y)2 | x·log(y) |
| 622.9 | 1.59 | 388004.41 | 2.53 | 989.93 |
| 658 | 1.65 | 432964 | 2.72 | 1084.82 |
| 700.4 | 1.7 | 490560.16 | 2.91 | 1194.01 |
| 740.6 | 1.72 | 548488.36 | 2.97 | 1275.88 |
| 774.4 | 1.72 | 599695.36 | 2.97 | 1334.11 |
| 816.2 | 1.67 | 666182.44 | 2.78 | 1361.18 |
| 853.5 | 1.61 | 728462.25 | 2.59 | 1373.66 |
| 876.8 | 1.55 | 768778.24 | 2.39 | 1356.9 |
| 900 | 1.53 | 810000 | 2.33 | 1373.45 |
| 951.4 | 1.61 | 905161.96 | 2.59 | 1531.22 |
| 1007.9 | 1.69 | 1015862.41 | 2.84 | 1699.72 |
| 1004.8 | 1.44 | 1009623.04 | 2.06 | 1441.97 |
| 1010.8 | 1.44 | 1021716.64 | 2.06 | 1450.58 |
| 1056.2 | 1.53 | 1115558.44 | 2.33 | 1611.82 |
| 1105.4 | 1.48 | 1221909.16 | 2.2 | 1637.77 |
| 1162.3 | 1.55 | 1350941.29 | 2.39 | 1798.73 |
| 1200.7 | 1.55 | 1441680.49 | 2.39 | 1858.16 |
| 1209.5 | 1.36 | 1462890.25 | 1.85 | 1646.1 |
| 1248.6 | 1.28 | 1559001.96 | 1.64 | 1599.37 |
| 1254.4 | 1.28 | 1573519.36 | 1.64 | 1606.8 |
| 1284.6 | 1.39 | 1650197.16 | 1.92 | 1780.83 |
| 20439.4 | 32.32 | 20761197.38 | 50.1 | 31007.03 |
1. Параметры уравнения регрессии.
Выборочные средние.
![]()
![]()
![]()
Выборочные дисперсии:
![]()
![]()
Среднеквадратическое отклонение
![]()
![]()
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты.
Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.
Коэффициент эластичности находится по формуле:
Эx=x·ln(b) = 973.3·(-0.000515) = -0.5
Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
![]()
Т.е. увеличение x на величину среднеквадратического отклонения Sx приведет к уменьшению среднего значения Y на 0.79 среднеквадратичного отклонения Sy.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
![]()
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным.
![]()
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве регрессии.
1.5. Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
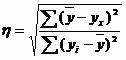
![]()
где ∑(y-yx)² = 0.37-0.14 = 0.23
Индекс корреляции.
Величина индекса корреляции R находится в границах от 0 до 1. Чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
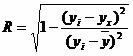
![]()
Полученная величина свидетельствует о том, что фактор x существенно влияет на y
Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции:
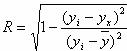
Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции rxy.
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
1.6. Индекс детерминации.
Величину R2 (равную отношению объясненной уравнением регрессии дисперсии результата у к общей дисперсии у) для нелинейных связей называют индексом детерминации.
Чаще всего, давая интерпретацию индекса детерминации, его выражают в процентах.
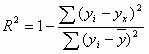
![]()
т.е. в 62.05 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - средняя. Остальные 37.95 % изменения Y объясняются факторами, не учтенными в модели.
Для оценки качества параметров регрессии построим расчетную таблицу (табл. 2)
| x | log(y) | y(x) | (yi-ycp)2 | (y-y(x))2 | (xi-xcp)2 | |y - yx|:y |
| 622.9 | 1.59 | 1.72 | 0.00253 | 0.017 | 122783.5 | 0.082 |
| 658 | 1.65 | 1.7 | 0.012 | 0.00278 | 99417.09 | 0.032 |
| 700.4 | 1.7 | 1.68 | 0.0275 | 0.000634 | 74477.01 | 0.0148 |
| 740.6 | 1.72 | 1.66 | 0.0338 | 0.00409 | 54151.51 | 0.0371 |
| 774.4 | 1.72 | 1.64 | 0.0338 | 0.00662 | 39563.1 | 0.0472 |
| 816.2 | 1.67 | 1.62 | 0.0166 | 0.00229 | 24681.91 | 0.0287 |
| 853.5 | 1.61 | 1.6 | 0.00498 | 7.7E-5 | 14353.18 | 0.00546 |
| 876.8 | 1.55 | 1.59 | 7.5E-5 | 0.00169 | 9313.17 | 0.0265 |
| 900 | 1.53 | 1.58 | 0.000165 | 0.00256 | 5373.59 | 0.0332 |
| 951.4 | 1.61 | 1.55 | 0.00498 | 0.00351 | 479.82 | 0.0368 |
| 1007.9 | 1.69 | 1.52 | 0.0218 | 0.0273 | 1196.83 | 0.098 |
| 1004.8 | 1.44 | 1.52 | 0.0108 | 0.00767 | 991.95 | 0.061 |
| 1010.8 | 1.44 | 1.52 | 0.0108 | 0.00714 | 1405.89 | 0.0589 |
| 1056.2 | 1.53 | 1.5 | 0.000165 | 0.000893 | 6871.62 | 0.0196 |
| 1105.4 | 1.48 | 1.47 | 0.00328 | 0.000117 | 17449.15 | 0.00729 |
| 1162.3 | 1.55 | 1.44 | 7.5E-5 | 0.0113 | 35719.2 | 0.0685 |
| 1200.7 | 1.55 | 1.42 | 7.5E-5 | 0.0158 | 51708.59 | 0.0813 |
| 1209.5 | 1.36 | 1.42 | 0.0317 | 0.00316 | 55788.19 | 0.0413 |
| 1248.6 | 1.28 | 1.4 | 0.0665 | 0.0135 | 75787.47 | 0.0906 |
| 1254.4 | 1.28 | 1.39 | 0.0665 | 0.0128 | 79014.53 | 0.0883 |
| 1284.6 | 1.39 | 1.38 | 0.0233 | 6.2E-5 | 96904.73 | 0.00567 |
| 20439.4 | 32.32 | 32.32 | 0.37 | 0.14 | 867432.03 | 0.96 |
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
![]()
![]()
S2y = 0.00742 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
![]()
Sy = 0.0861 - стандартная ошибка оценки (стандартная ошибка регрессии).
Sa - стандартное отклонение случайной величины a.
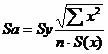
![]()
Sb - стандартное отклонение случайной величины b.
![]()
![]()
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения. Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
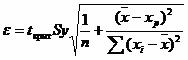
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и Xp = 600
![]()
(2.04 -0.000515*600 ± 0.0823)
(1.65;1.81)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bxi ± ε)
где
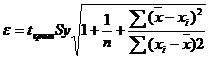
![]()
tкрит (n-m-1;α/2) = (19;0.025) = 2.093
| xi | y = 2.04 -0.000515xi | εi | ymin= y - εi | ymax= y + εi |
| 622.9 | 1.72 | 0.2 | 1.52 | 1.92 |
| 658 | 1.7 | 0.19 | 1.51 | 1.9 |
| 700.4 | 1.68 | 0.19 | 1.49 | 1.87 |
| 740.6 | 1.66 | 0.19 | 1.47 | 1.85 |
| 774.4 | 1.64 | 0.19 | 1.45 | 1.83 |
| 816.2 | 1.62 | 0.19 | 1.43 | 1.81 |
| 853.5 | 1.6 | 0.19 | 1.41 | 1.79 |
| 876.8 | 1.59 | 0.19 | 1.4 | 1.77 |
| 900 | 1.58 | 0.19 | 1.39 | 1.76 |
| 951.4 | 1.55 | 0.18 | 1.37 | 1.73 |
| 1007.9 | 1.52 | 0.18 | 1.34 | 1.71 |
| 1004.8 | 1.52 | 0.18 | 1.34 | 1.71 |
| 1010.8 | 1.52 | 0.18 | 1.33 | 1.7 |
| 1056.2 | 1.5 | 0.19 | 1.31 | 1.68 |
| 1105.4 | 1.47 | 0.19 | 1.28 | 1.66 |
| 1162.3 | 1.44 | 0.19 | 1.25 | 1.63 |
| 1200.7 | 1.42 | 0.19 | 1.23 | 1.61 |
| 1209.5 | 1.42 | 0.19 | 1.23 | 1.61 |
| 1248.6 | 1.4 | 0.19 | 1.2 | 1.59 |
| 1254.4 | 1.39 | 0.19 | 1.2 | 1.59 |
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
С помощью МНК мы получили лишь оценки параметров уравнения регрессии, которые характерны для конкретного статистического наблюдения (конкретного набора значений x и y).
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля.
Чтобы проверить, значимы ли параметры, т.е. значимо ли они отличаются от нуля для генеральной совокупности используют статистические методы проверки гипотез.
В качестве основной (нулевой) гипотезы выдвигают гипотезу о незначимом отличии от нуля параметра или статистической характеристики в генеральной совокупности. Наряду с основной (проверяемой) гипотезой выдвигают альтернативную (конкурирующую) гипотезу о неравенстве нулю параметра или статистической характеристики в генеральной совокупности.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
В случае если основная гипотеза окажется неверной, мы принимаем альтернативную. Для проверки этой гипотезы используется t-критерий Стьюдента.
Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактическим) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике).
Табличное значение определяется в зависимости от уровня значимости (α) и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n-число наблюдений.
Если фактическое значение t-критерия больше табличного (по модулю), то основную гипотезу отвергают и считают, что с вероятностью (1-α) параметр или статистическая характеристика в генеральной совокупности значимо отличается от нуля.
Если фактическое значение t-критерия меньше табличного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля при уровне значимости α.
tкрит (n-m-1;α/2) = (19;0.025) = 2.093
Поскольку 5.15 > 2.093, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 22.19 > 2.093, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b - tкрит Sb; b + tкрит Sb)
(-0.000515 - 2.093·9.2E-5; -0.000515 + 2.093·9.2E-5)
(-0.000725;-0.000306)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a - tкрит Sa; a + tкрит Sa)
(2.04 - 2.093·0.0919; 2.04 + 2.093·0.0919)
(1.85;2.23)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистика. Критерий Фишера.
Индекс детерминации R2 используется для проверки существенности уравнения нелинейной регрессии в целом.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
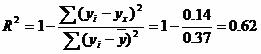
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=19, Fтабл = 4.38
Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством:
Дисперсионный анализ.
При анализе качества модели регрессии используется теорема о разложении дисперсии, согласно которой общая дисперсия результативного признака может быть разложена на две составляющие – объясненную и необъясненную уравнением регрессии дисперсии.
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
∑(yi - y)2 = ∑(y(x) - ycp)2 + ∑(y - y(x))2
где
∑(yi - y)2 - общая сумма квадратов отклонений;
∑(y(x) - ycp)2 - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
∑(y - y(x))2 - остаточная сумма квадратов отклонений.
| Источник вариации | Сумма квадратов | Число степеней свободы | Дисперсия на 1 степень свободы | F-критерий |
| Модель | 0.23 | 1 | 0.23 | 31.07 |
| Остаточная | 0.14 | 19 | 0.00737 | 1 |
| Общая | 0.37 | 21-1 |
Показатели качества уравнения регрессии.
| Показатель | Значение |
| Коэффициент детерминации | 0.62 |
| Средний коэффициент эластичности | -0.000515 |
| Средняя ошибка аппроксимации | 4.59 |