Тест Голдфелда-Квандта

В данном случае предполагается, что стандартное отклонение σ_i = σ(ε_i) пропорционально значению x_i переменной X в этом наблюдении, т.е. σ²_i = σ²x²_i , i = 1,2,…,n.

Тест Голдфелда-Квандта состоит в следующем:

Все n наблюдений упорядочиваются по величине X.
Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей k,(n-2k),k соответственно.
Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Для парной регрессии Голдфелд и Квандт предлагают следующие пропорции: n=30,k=11; n=60,k=22. Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии по первой подвыборке (рассчитываемая как 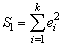) будет существенно меньше дисперсии регрессии по третьей подвыборке (рассчитываемой как ).
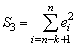Для сравнения соответствующих дисперсий строится соответствующая F-статистика:

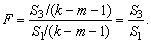
Здесь (k – m - 1)– число степеней свободы соответствующих выборочных дисперсий (m – количество объясняющих переменных в уравнении регрессии).
Построенная F-статистика имеет распределение Фишера с числом степеней свободы v₁ = v₂ = n – m - 1.
Если 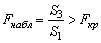(где F_кр = F_α_,_v_1,_v₂, определяется из таблиц, α– выбранный уровень значимости), то гипотеза об отсутствии гетероскедастичности отклоняется.
Этот же тест может использоваться при предположении об обратной пропорциональности между σ_i и значениями объясняющей переменной. При этом статистика Фишера имеет вид: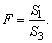

Для множественной регрессии данный тест обычно проводится для той объясняющей переменной, которая в наибольшей степени связана с σ_i. При этом k должно быть больше, чем (m+1). Если нет уверенности относительно выбора переменной X_j, то данный тест может осуществляться для каждой из объясняющих переменных.

Тест Голдфелда-Квандта онлайн

Пример. 1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК:
a₀n + a₁∑x = ∑y
a₀∑x + a₁∑x² = ∑y•x
Для наших данных система уравнений имеет вид:
14a₀ + 520.3a₁ = 178.1
520.3a₀ + 19991.23a₁ = 6651.61
Из первого уравнения выражаем а₀ и подставим во второе уравнение
Получаем a₀ = 0.0499, a₁ = 10.87

x	y	x²	y²	x • y	y(x)	(y-y(x))²
25.5	14.5	650.25	210.25	369.75	12.14	5.57
26.5	11.3	702.25	127.69	299.45	12.19	0.79
27.2	14.7	739.84	216.09	399.84	12.22	6.13
29.6	10.2	876.16	104.04	301.92	12.34	4.6
35.7	13.5	1274.49	182.25	481.95	12.65	0.73
38.6	9.9	1489.96	98.01	382.14	12.79	8.37
39	12.4	1521	153.76	483.6	12.81	0.17
39.3	8.6	1544.49	73.96	337.98	12.83	17.88
40	10.3	1600	106.09	412	12.86	6.57
41.9	13.9	1755.61	193.21	582.41	12.96	0.89
42.5	14.9	1806.25	222.01	633.25	12.99	3.66
44.2	11.6	1953.64	134.56	512.72	13.07	2.17
44.8	21.5	2007.04	462.25	963.2	13.1	70.52
45.5	10.8	2070.25	116.64	491.4	13.14	5.46
520.3	178.1	19991.23	2400.81	6651.61	178.1	133.49

Здесь S₁ = 133.49

2. Оценим регрессию для третьей подвыборки. Система уравнений МНК:
a₀n + a₁∑x = ∑y
a₀∑x + a₁∑x² = ∑y•x
Для наших данных система уравнений имеет вид:
14a₀ + 1146.6a₁ = 288.8
1146.6a₀ + 94248.54a₁ = 23640.18
Из первого уравнения выражаем а₀ и подставим во второе уравнение
Получаем a₀ = -0.0367, a₁ = 23.63

x	y	x²	y²	x • y	y(x)	(y-y(x))²
73.8	14.3	5446.44	204.49	1055.34	20.93	43.9
74.7	21.8	5580.09	475.24	1628.46	20.89	0.82
75.8	26.1	5745.64	681.21	1978.38	20.85	27.54
76.9	20	5913.61	400	1538	20.81	0.66
79.2	19.8	6272.64	392.04	1568.16	20.73	0.86
81.5	21.2	6642.25	449.44	1727.8	20.64	0.31
82.4	29	6789.76	841	2389.6	20.61	70.39
82.8	17.3	6855.84	299.29	1432.44	20.6	10.86
83	23.5	6889	552.25	1950.5	20.59	8.48
85.9	22	7378.81	484	1889.8	20.48	2.3
86.4	18.3	7464.96	334.89	1581.12	20.46	4.68
86.9	13.7	7551.61	187.69	1190.53	20.45	45.5
88.3	14.5	7796.89	210.25	1280.35	20.39	34.74
89	27.3	7921	745.29	2429.7	20.37	48.05
1146.6	288.8	94248.54	6257.08	23640.18	288.8	299.09

Здесь S₃ = 299.09
Fkp(1,38) = 4.08
Строим F-статистику:
F = 299.09/133.49 = 2.24
Поскольку F < F_kp = 4.08, то гипотеза об отсутствии гетероскедастичности принимается.

Тест Голдфелда-Квандта

Правила ввода данных

Поиск

Процесс

Сообщение