Линейное программирование. Теория
- Классификация экономических моделей
- Линейное программирование
- Микроэкономические модели линейного программирования
- Задача составления кормовой смеси или задача о диете
- Производственная задача
- Задача о раскрое или минимизации отходов (обрезков)
- Задача об использовании мощностей
- Задача о банке
- Модели линейного программирования для решения задач раскроя
- Модель оптимизации рекламной кампании
- Динамические модели линейного программирования
Графический метод решения задач линейного программирования
- Решение систем линейных неравенств графически
- Решение задачи линейного программирования графически
- Графический анализ чувствительности
Симплекс-метод решения задач линейного программирования
- Формулировка основных типов задач ЛП, построение их математических моделей
- Каноническая форма задач линейного программирования
- Симплексный метод решения задач линейного программирования
- Поиск первоначального опорного плана
- Виды записи симплекс-метода
- Двухфазный симплекс-метод
- Матричное описание симплекс-метода
- M-задача
- Симплекс-метод с естественным базисом
- Дробно-линейное программирование
- Построение математической модели для симплекс-задачи
Двойственность в задачах линейного программирования
- Теоремы двойственности. Двойственность в задачах линейного программирования
- Экономическая интерпретация двойственной задачи и теории двойственности (Анализ решения задачи линейного программирования с помощью теории двойственности)
- Симметричные двойственные задачи
- Несимметричные двойственные задачи
Целочисленное программирование
- Метод отсечения. Алгоритм Гомори
- Алгоритм Гомори для частично целочисленной задачи линейного программирования
- Целочисленное программирование
- Метод ветвей и границ
Задачи линейного параметрического программирования
Словарь по линейному программированию
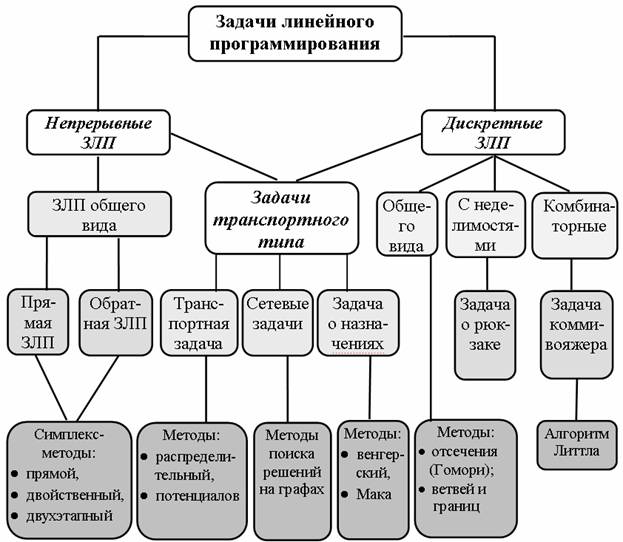
Все алгоритмы решения ЗЛП опираются на каноническую форму задачи. Поэтому число искомых переменных канонической задачи будет больше, чем исходной.
Список рекомендуемой литературы
- Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. Учебное пособие. – М.,Финансы и статистика, 2005
- Беспалов М.С. Линейное программирование. Владимир: ВлГУ. 1999
- Галкин А.А. Математическая экономика. Владимир: ВлГУ. 2006
- Глухов В.В.Математические методы и модели для менеджмента: учебное пособие. – СПБ;М.;Краснодар:Лань,2005
- Грицюк С.Н.Математические методы и модели в экономике: учебник.- Ростов н/Д:Феникс, 2007
- Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М.,Изд-во «Дело и сервис», 2004.
- Исследование операций в экономике. Учебное пособие для вузов/Под ред. проф.Н.Ш.Кремера. – М., ЮНИТИ, 2005.
- Кузнецов Б.Т. Математические методы и модели исследования операций: учебное пособие. М.:ЮНИТИ – ДАНА, 2005
- Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М.: Высшая школа. 1980.
- Кундышева Е.С. Математическое моделирование в экономике: Учебное пособие. – М., Издательско-торговая корпорация «Дашков и Ко», 2004.
- Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учеб.- М.:Дело, 2001
- Орехов А.М. Методы экономических исследований: учебное пособие. – М:ИНФРА – М, 2006
- Орлова А.М. Экономико-математическое моделирование: практическое пособие по решению задач – М.: Вузовский учебник, 2007
- Просветов Г.И.Математические методы в экономике: учебно-методическое пособие. М, Изд-во РДЛ, 2007
- Справочник по математике для экономистов. Под ред. В.И. Ермакова. М.: Высшая школа. 1987.
- Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. - М.: Финансы и статистика, 2005.
- Шевченко В.Н., Золотых Н.Ю. Линейное и целочисленное линейное программирования. - Нижний Новгород: Изд-во Нижегородского государственного университета им. Н.И. Лобачевского, 2004. - 154 с.
- Экономико-математическое моделирование: учебник / ред.И.Н. Дрогобыцкий. М.:Экзамен, 2006
- Экономико-математические методы и модели:учебное пособие / под ред. С.И.Макарова. – М.:КНОРУС, 2007