Задача о назначениях в Excel

1. Постановка экономической задачи (исходные данные варианта)
Мастер должен назначить на 5 типовых операций 7 рабочих. Время, которое затрачивают рабочие на выполнение каждой операции, приведено в таблице.

Рабочие	Операции
Рабочие	О1	О2	О3	О4	О5
Р1	25	22	30	24	31
Р2	32	–	14	34	30
Р3	35	–	32	31	28
Р4	36	27	14	24	30
Р5	35	25	30	22	–
Р6	34	33	26	14	19
Р7	34	27	30	37	37

Знак «–» означает, что рабочий не может выполнять данную операцию.
Определите расстановку рабочих по операциям, при которой суммарное время на выполнение всех работ будет наименьшим.

2. Экономико-математическая модель задачи
Данная задача является задачей о назначениях и реализуется как частный случай транспортной задачи. Видно, что число рабочих (7) превышает количество операций, которое они должны выполнить (5). Следовательно, задача является открытой, и решать ее целесообразно путем приведения к закрытой задаче, для чего вводятся две фиктивные операции — О6 и О7. Время на выполнение фиктивных операций равно нулю, так как они фактически не выполняются.
Представим исходные данные закрытой задачи в виде таблицы:

Рабочие	Операции
Рабочие	О1	О2	О3	О4	О5	О6	О7
Р1	25	22	30	24	31	0	0
Р2	32	1000	14	34	30	0	0
Р3	35	1000	32	31	28	0	0
Р4	36	27	14	24	30	0	0
Р5	35	25	30	22	1000	0	0
Р6	34	33	26	14	19	0	0
Р7	34	27	30	37	37	0	0

В ячейках с заливкой находятся затраты времениc_ij на выполнениеi–м рабочим (i=1, …, 7) j–й операции (j=1, …, 7). В ячейки, в которых был знак «–», вместо него помещены числа, существенно превышающие другие затраты времени (1000), чтобы при решении задачи соответствующие значения переменных оказались заведомо равными нулю.
Обозначим черезx_ij факт назначенияi–го рабочего на выполнениеj–й операции(1 — если рабочий назначен, 0 — если не назначен). Математическая модель задачи имеет вид:
Найти такие значения x_ij, чтобы суммарное время на выполнение всех работ было наименьшим:

;
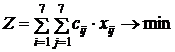и при этом:

каждый рабочий должен быть назначен только на одну операцию:
;
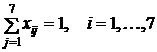на каждую операцию должен быть назначен только один рабочий:
;
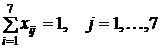переменные задачи являются двоичными:
.

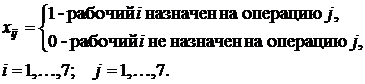3. Компьютерная технология получения оптимального решения
Данную задачу решаем с помощью калькулятора и надстройки Поиск решения табличного процессора MS Excel. В ячейки рабочего листа программного средства вводятся исходные данные и формулы:

В ячейки B5:H11 вводятся затраты времени, необходимого рабочим на выполнение операций;
В ячейках B15:H21 находятся значения переменных x_ij. Первоначально в них помещаются произвольные числа, например, единицы.
В ячейки I15:I21 вводятся формулы для расчета сумм значений переменных в соответствующих строках. Например, в ячейке I15 формула имеет вид: =СУММ(B15:H15).
В ячейки B22:H22 вводятся формулы для расчета сумм значений переменных в соответствующих столбцах. Например, в ячейке B22 формула имеет вид: =СУММ(B15:B21).
В ячейку B24 вводится выражение целевой функции задачи с использованием встроенной функцииEXCEL «СУММПРОИЗВ». Аргументами этой функции являются блоки ячеек, содержащие затраты времени и значения переменных: =СУММПРОИЗВ(B5:H11;B15:H21).

Лист исходных данных, таким образом, имеет вид:

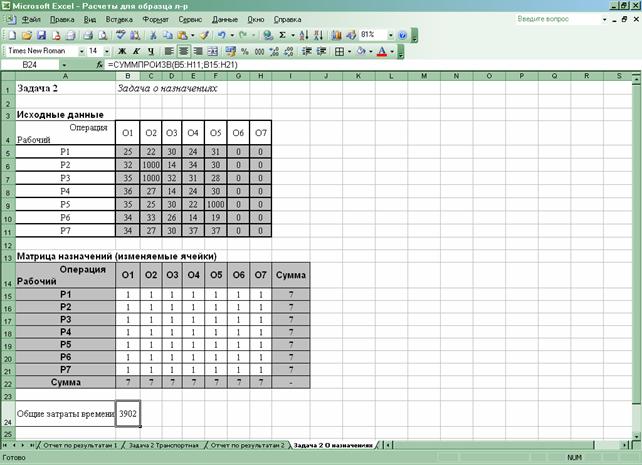
После ввода исходных данных запускается надстройка «Поиск решения» (меню «Сервис» ® «Поиск решения…») и заполняются необходимые поля в панели надстройки:

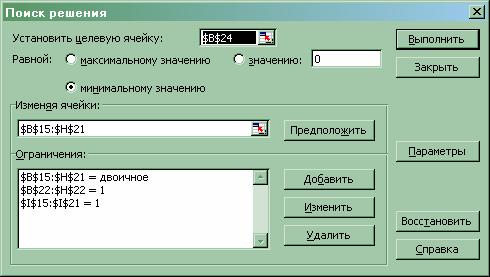
В панели «Параметры поиска решения» указывается, что модель задачи оптимизации является линейной, и задается условие неотрицательности переменных:

4. Решение задачи на ЭВМ
После запуска надстройки «Поиск решения» на выполнение было получено сообщение об успешном решении задачи оптимизации:

В окне «Тип отчета» выбираем пункт «Результаты».

Рабочий лист MS Excel, содержащий результаты решения имеет вид:

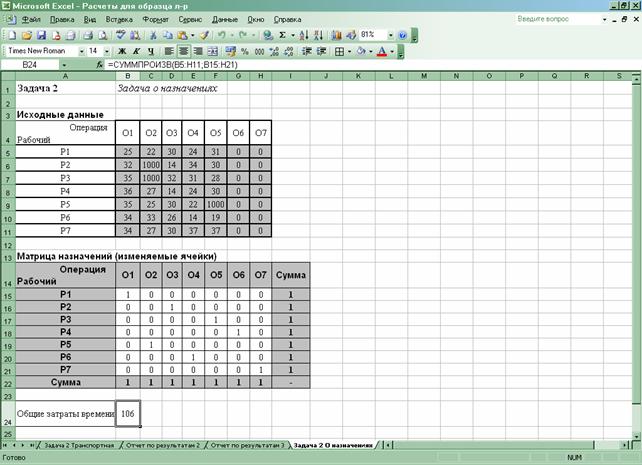
5. Предложения (рекомендации) лицу, ответственному за принятие решений, по оптимальному управленческому поведению
Таким образом, чтобы суммарные затраты времени на выполнение операций были наименьшими, следует назначить:

рабочего 1 на выполнение операции 1;
рабочего 2 на выполнение операции 3;
рабочего 3 на выполнение операции 5;
рабочего 4 на выполнение фиктивной операции 6;
рабочего 5 на выполнение операции 2;
рабочего 6 на выполнение операции 4;
рабочего 7 на выполнение фиктивной операции 7.
Рабочие 4 и 7, назначенные на выполнение фиктивных операций, фактически не работают.

Суммарное время на выполнение всех операций составит 106 ч.

Задача о назначениях в Excel

Правила ввода данных

Поиск

Процесс

Сообщение