Как построить график функции
С помощью программы Desmos можно построить график одной или нескольких функций. Каждая новая функция вводится с новой строки.
Для добавления одной точки достаточно указать, например, A=(3.5,6.1).
Для задания области (например,
Примеры ограничений для функции:
Для задания области (например,
1≤x≤7) используйте пределы <= или >=.
Примеры ограничений для функции:
- tan^(-1)(x-2)+1.5 {0<x<3}
- y=2 {0<x<2.5}
- x=2.5 {0<y<2}

Чтобы настроить вид координатной сетки (пределы по осям и стрелки) используйте  .
.

 .
.

Для добавления точек с координатами (x,y) используйте + и вид table


| Прямая зависимость | y=x^2+1 | |
| Обратная зависимость | x=sqrt(3-y^2) | |
| Неравенства | y>log(x) x≤2y+3 |  |
| Полярная система координат | r=sin(5*θ), переменная theta | 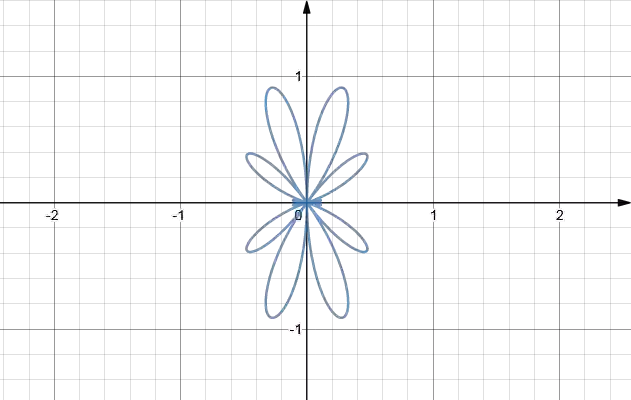 |
| Кусочно-заданные функции | y={1<x<2} x={-π<y<π:sin(y)} y=(x-4)^2-3{2<x<7} |  |
| Точка | (1,0) | |
| Группа точек | (1,1), (2,2), (3,3) | |
| Функции с параметром | (sin(2*t),cos(3*t)) | |
| Сложные функции | x^2+y^2=1 y^2+sin(x)/y+x=2 |
| Подвижная точка | (a,b) | |
| Анимация | a=-7 (a*t-sin(a*t),1-cos(a*t)) (x-a)^2+(y-1)^2=1 (a-sin(a),1-cos(a)) |
Трехмерные графики функции
Построить графики (в том числе и трехмерные) можно также, используя следующий сервис Wolframe. Например, построить график функцииcosx + esinx+x3. Записываем как cos(x)+exp((sin(x)+x^3)) и нажимаем кнопку Построить график.
Чтобы построит два графика в одних координатах, например,
y=3x-1, y=x2-2x+5, указываем: 3*x-1,x^2-2*x+5. Также можно задать пределы отображения по оси X (ось абсцисс).
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3).
Правила ввода функций:
Также можно начертить график по точкам. Необходимо вставить данные для X (первый столбец) и Y (второй и последующие столбцы).
Построение графика функции в Excel осуществляется в два этапа:
- На первом этапе при заданном интервале [a;b] и шаге h рассчитываются значения функции
y=f(x). - На втором этапе с помощью инструмента Excel Мастер диаграмм строится визуализация рассчитанных значений.
Чтобы построить трехмерный график в Excel, необходимо указать функцию f(x,y), пределы по x и y и шаг сетки h.
Принципы и способы построения графика функции
График любой функции можно построить прямыми вычислениями значения функцииy=f(x) и методом дифференциального исчисления.
- При прямом вычислении значений функции
y=f(x)необходимо задать интервал [a;b] вычислений и шаг h. Получается таблица, по которой можно построить график.
Например, определим для функцииy=x*e2x/3+4интервал [-3;7], на котором будем отображать найденные точки. Чем меньше шаг h, тем точнее график функции (другими словами, тем точнее аппроксимация). Например, при h=2 количество точек для построения равноN=(7-(-3))/2+1=6(-3; -1; 1; 3; 5; 7), а при h=0.1 ужеN=(7-(-3))/0.1+1=101. - Построение графика функции методом дифференциального исчисления предполагает схематичное построение, используя свойства функции.
Прикладное применение графика функции
Среди задач, в которых необходимо построить график функции можно выделить:- Построение графика функции методом дифференциального исчисления.
- Приближенное решение алгебраических уравнений.
- Построение тренда.
- Построение уравнения регрессии.
- Построение уравнения касательной к графику функции.
- Построение уравнения нормали к графику функции:
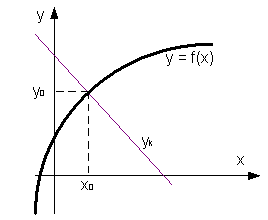 .
.
- Построение плотности и функции распределения дискретной случайной величины.
- Построение плотности и функции распределения непрерывной случайной величины.
- Построение прерывной функции при определении точек разрыва:
 .
.
- Площадь фигуры, ограниченной линиями:
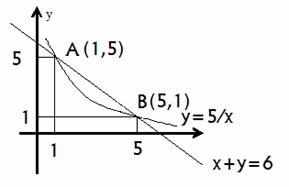
Построить пирамиду ABCD по координатам можно здесь.
