Математическое ожидание непрерывной случайной величины
Математическое ожидание непрерывной случайной величины X, возможные значения которой принадлежат всей оси Ох, определяется равенством:
Дисперсия непрерывной случайной величины X (Var[X]), возможные значения которой принадлежат всей оси Ох, определяется равенством:
Назначение сервиса. Онлайн калькулятор предназначен для решения задач, в которых заданы либо плотность распределения f(x), либо функция распределения F(x) (см. пример). Обычно в таких заданиях требуется найти математическое ожидание, среднее квадратическое отклонение, построить графики функций f(x) и F(x).
Задана функция распределения F(x)
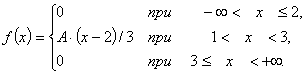
Задана функция распределения F(x): 
Непрерывная случайна величина задана плотностью вероятностей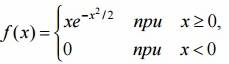 
(закон распределения Релея – применяется в радиотехнике). Найти M(x), D(x).
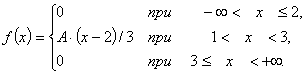
В качестве неизвестного параметра используйте заглавную букву A. Например,
c(x2+2x-1) ≡ A*(x^2+2*x-1)
?>
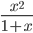≡ x^2/(1+x)
cos2(2x+1) ≡ (cos(2*x+1))^2
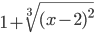≡ 1+(x-2)^(2/3)
Случайную величину X называют непрерывной, если ее функция распределения F(X)=P(X < x) непрерывна и имеет производную.
Функция распределения непрерывной случайной величины применяется для вычисления вероятностей попадания случайной величины в заданный промежуток:
P(α < X < β)=F(β) - F(α)
причем для непрерывной случайной величины не имеет значения, включаются в этот промежуток его границы или нет:
P(α < X < β) = P(α ≤ X < β) = P(α ≤ X ≤ β)
Плотностью распределения непрерывной случайной величины называется функция
f(x)=F’(x), производная от функции распределения.
Свойства плотности распределения
1. Плотность распределения случайной величины неотрицательна (f(x) ≥ 0) при всех значениях x.2. Условие нормировки:
Геометрический смысл условия нормировки: площадь под кривой плотности распределения равна единице.
3. Вероятность попадания случайной величины X в промежуток от α до β может быть вычислена по формуле
Геометрически вероятность попадания непрерывной случайной величины X в промежуток (α, β) равна площади криволинейной трапеции под кривой плотности распределения, опирающейся на этот промежуток.
4. Функция распределения выражается через плотность следующим образом:
Значение плотности распределения в точке x не равно вероятности принять это значение, для непрерывной случайной величины речь может идти только о вероятности попадания в заданный интервал. Пусть [x, x + Δx) — интервал произвольно малой длины Δx > 0. Вероятность попадания случайной величины в этот интервал приближенно равна произведению значения плотности распределения в точке x на длину этого интервала: f(x)Δx, то есть вероятность пропорциональна длине интервала, причем коэффициент пропорциональности равен значению плотности распределения в точке x (рис.).
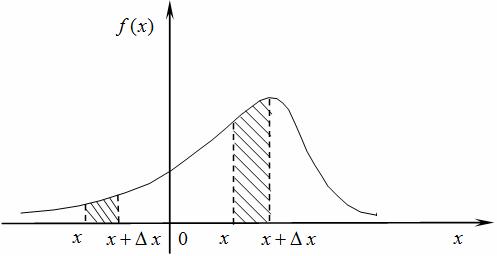
Числовые характеристики непрерывной случайной величины находятся по формулам, похожим на формулы для дискретной случайной величины, но везде знак суммы заменяется на знак интеграла, а вероятность pi на дифференциальный элемент вероятности f(x)dx.
Математическое ожидание непрерывной случайной величины равно
Дисперсия непрерывной случайной величины есть Var(x)=
Все свойства математического ожидания и дисперсии, сформулированные для дискретных случайных величин, сохраняются и для непрерывных случайных величин.
Пример №1. Случайная величина Х задана функцией распределения F(x):
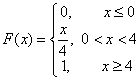
Найдем плотность распределения f(x), как производную от функции распределения F(x):
f(x) = dF(x)/dx = 1/4
Математическое ожидание.
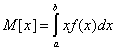
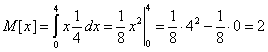
Дисперсия.
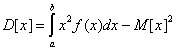
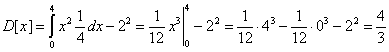
Пример №2. Плотность распределения непрерывной случайной величины X имеет вид
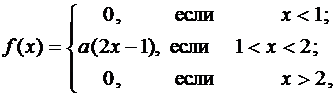
где a - параметр.
Для непрерывной случайной величины X найти: а) значение параметра a, при котором f(x) является плотностью распределения случайной величины X; б) функцию распределения F(x); в) математическое ожидание Mx и дисперсию Dx; г) P{X≥1,5}.
Построить графики функции распределения F(x) и плотности распределения f(x).
Пример №3. Непрерывная случайная величина имеет плотность распределения f(x). Найти величину с, интегральную функцию распределения, математическое ожидание и среднее квадратическое отклонение этой случайной величины.
Примечание. Очень часто при нахождении математического ожидания и дисперсии применяют формулу интегрирования по частям.