Математический анализ
В ниже приведенных онлайн-калькуляторах решение сохраняется в формате Word с отображением всех исходных формул.Линейная алгебра
- Определитель матрицы.
- Матричный калькулятор:
3A-BC+A-1 - Методы решения системы уравнений: метод Гаусса, метод Крамера, метод обратной матрицы и другие.
- Координаты вектора в новом базисе. Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
- Приведение кривой второго порядка к каноническому виду
- Собственные числа матрицы
- Выделение полного квадрата (a•x2 + b•x + c = 0)
- Метод неопределенных коэффициентов (преобразовать в сумму простейших дробей):

- Формула дискриминанта. Данный вид калькулятора используется для нахождения дискриминанта и корней функции.
- Деление многочленов столбиком. Данная процедура, в частности, поможет при нахождении интегралов.
- Решение пределов.
Комплексные числа
- Комплексные числа в тригонометрической и показательной формах
- Извлечение корня из комплексных чисел используется, например, при нахождении уравнений типа
w3 - z = 0.
Дифференциальное исчисление
- Найти производную cosx + esinx+x3x
- Дифференциал функции
- Правило Лопиталя при вычислении пределов.
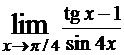
- Уравнение касательной к графику функции, уравнение нормали
- Наибольшее и наименьшее значение функции одной переменной. Калькулятор вычисляет экстремум функции. Интервалы возрастания и убывания функции. Интервалы выпуклости и вогнутости графика функции. Точки перегиба.
- Асимптоты функции. Определение наклонных, вертикальных и горизонтальных асимптот.
- Построение графика функции методом дифференциального исчисления
Дифференциальные уравнения
- Дифференциальные уравнения:
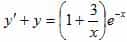 ,
, 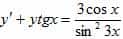 .
.
- Линейные дифференциальные уравнения (решение однородных дифференциальных уравнений
y''-2y'+y = e2x)
Интегральное исчисление
- Площадь фигуры, ограниченной линиями:
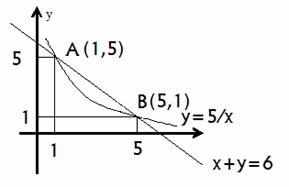
- Вычисление интегралов (Таблица интегралов)
- Работа силы при перемещении вдоль дуги линии: Найти работу силы F при перемещении вдоль дуги линии L от точки M0 до точки M1.
Степенные ряды
- Определить сходимость или расходимость ряда
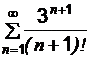
- Определить область сходимости степенного ряда
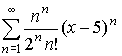
- Разложить в ряд Тейлора
- Разложение функции в ряд Фурье: Разложить в ряд Фурье функцию f(x)=1+x на отрезке [-1, 1]. Построить графики частичных сумм S0, S1, S2.
| Найти корни уравнения | x2 - 3x + 4 = 0 |
| Разложить на множители | x2 - 3x + 4 = 0 |
Типовые примеры задач математического анализа
Примечание: все ссылки, расположенные внутри решения данной работы, ведут на соответствующие онлайн-калькуляторы.Задача 1. Найти пределы функций с помощью правила Лопиталя.
Пределы
а)![]()
Решение.
Правило Лопиталя позволяет раскрывать неопределенность 0/0 и ∞ / ∞.
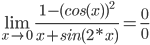
Применим правило Лопиталя, которое гласит, что предел отношения функций равен пределу отношения их производных.
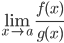
Для нашего примера: f(x) = 1-(cos(x))2, g(x) = x+sin(2•x)
Находим первую производную: f'(x) = 2•cos(x)•sin(x), g'(x) = 1+2•cos(2•x)
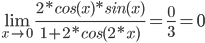
б) ![]()
Решение.
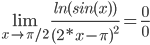
Для нашего примера:
f(x) = ln(sin(x))
g(x) = (2•x-π)2
Находим первую производную
f'(x) = cos(x)/sin(x)
g'(x) = -4•π+8•x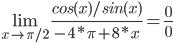
Находим вторую производную
f''(x) = -1-cos2(x)/sin2(x)
g''(x) = 8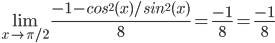
в) ![]()
г) ![]() .
.
Задача 2. Провести полное исследование и построить графики функций.
Функции
а) ![]() ;
;
Решение ищем по схеме:
- выяснение области определения функции;
- определение четности или нечетности функции;
- исследуется периодичность функции;
- расчет точек пересечения кривой с осями координат;
- находят точки разрыва функции и определяют их характер;
- исследования на экстремум;
Находим первую производную функции: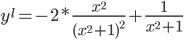
или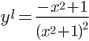
Приравниваем ее к нулю: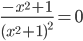
x1 = -1
x2 = 1
Вычисляем значения функции
f(-1) = -1/2
f(1) = 1/2
Ответ:
fmin = -1/2, fmax = 1/2
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную: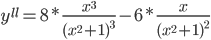
или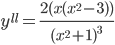
Вычисляем:
y''(-1) = 1/2>0 - значит точка x = -1 точка минимума функции.
y''(1) = -1/2<0 - значит точка x = 1 точка максимума функции. - поиск точек перегиба и интервалы выпуклости и вогнутости кривой;
- расчет асимптот кривой;
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: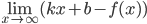
Находим коэффициент k: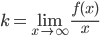
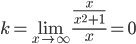
Находим коэффициент b: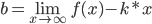
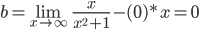
Получаем уравнение горизонтальной асимптоты:y = 0 - строят график исследуемой функции.
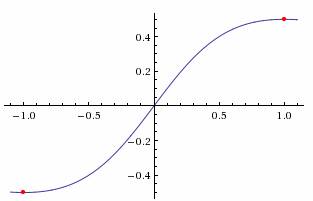
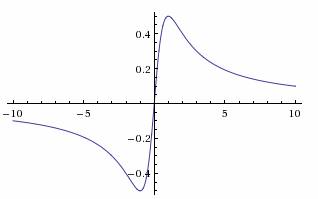
б)
Задача 3. Дано скалярное поле.
1) Составить уравнение линии u = C и построить её график.
2) Вычислить с помощью градиента производную скалярного поля u=u(x;y) в точке A по направлению вектора ![]() .
.
3) Найти наибольшую скорость изменения скалярного поля в точке A.
| С | Координаты т. А | Координаты т. В | |
| 4 | 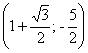
| 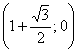
|
Задача 4. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Сделать чертеж.
Уравнения линий
y = -4x3; x=0; y=4
Задание 5. Найти общее решение дифференциального уравнения. Сделать проверку.
y′+2xy=3x2e-x2
Задание 6. Известно, что рыночный спрос Q и предложение S на некоторый товар линейно зависит от цены p: S=ap+b, Q=cp+d, где a, b, c, d-некоторые положительные постоянные. Исследование рынка показало, что скорость изменения цены ![]() пропорциональна превышению спроса над предложением с коэффициентом пропорциональности y. Напишите дифференциальное уравнение, характеризующее зависимость цены от времени t, и решите его при условии, что начальная цена товара имела значение p(0)=0,25.
пропорциональна превышению спроса над предложением с коэффициентом пропорциональности y. Напишите дифференциальное уравнение, характеризующее зависимость цены от времени t, и решите его при условии, что начальная цена товара имела значение p(0)=0,25.
Задание 7. Найти частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям.
y″-7y′+10y=0, y(0)=2, y′(0)=-1
Задание 8. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.
y″-2y′=3x2+1
Задание 9. Найти общее решение дифференциального уравнения.
x2y″-ln(x)=0
