Линейные дифференциальные уравнения с постоянными коэффициентами
см. также Решение линейных дифференциальных уравнений онлайнПоиск фундаментальной системы решений в общем случае является достаточно трудной задачей. Тем не менее, есть класс уравнений, для которого эта задача достаточно легко решается.
an(x)·y(n)+an-1(x)·y(n-1)+ ... + a1(x)·y′+a0(x)·y=b(x), (*)
Линейное дифференциальное уравнение (*) назовём уравнением с постоянными коэффициентами, если в этом уравнении коэффициенты постоянны, то есть ai(x)=const. Тогда соответствующее однородное уравнение L(y)=0 будет иметь вид
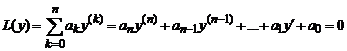. (6)
Решение уравнения (6) будем искать в виде y = erx. Тогда y' = r·erx, y'' = r2·erx,…, y(n) = rn·erx. Подставляя в (6), получаем
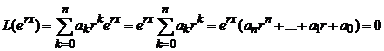.Так как erxнигде в нуль не обращается, то
. (7)
Уравнение (7) называется характеристическим уравнением линейного однородного дифференциального уравнения с постоянными коэффициентами.
Таким образом, нами доказана следующая теорема. Теорема. Функция y = erx является решением линейного однородного дифференциального уравнения с постоянными коэффициентами (6) тогда и только тогда, когда r есть корень характеристического уравнения (7).
Возможны ниже следующие случаи.
1. Все корни характеристического многочлена вещественны и различны. Обозначим их r1,r2,…,rn. Тогда получим n различных решений
y1 = er1x, y2 = er2x,…, yn = ernx (8)
уравнения (6). Докажем, что полученная система решений линейно независима. Рассмотрим её определитель Вронского
.
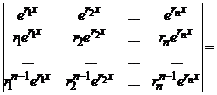
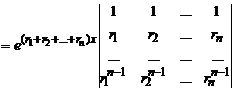Множитель e(r1+r2+..+rn)x в правой части W(er1x, er2x,…, ernx) нигде в нуль не обращается. Поэтому осталось показать, что второй сомножитель (определитель) не равен нулю. Допустим, что
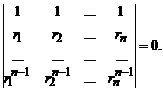
Тогда строки этого определителя линейно зависимы, т. е. существуют числа α1, α2, …, αn такие, что
, 
, … , 
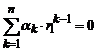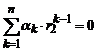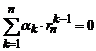.Таким образом, мы получили, что ri, i = 1,2,..,n есть n различных корней полинома (n-1)-й степени, что невозможно. Следовательно, определитель в правой части W(er1x, er2x,…, ernx) не равен нулю и система функций (8) образует фундаментальную систему решений уравнения (6) в случае, когда корни характеристичес-кого уравнения различны.
Пример №1. Для уравнения y''-3y' + 2y=0 корни характеристического уравнения r2 - 3r + 2 = 0 равны r1 = 1, r2 = 2 (корни были найдены через сервис нахождения дискриминанта). Следовательно, фундаментальную систему решений составляют функции y1 = ex, y2 = e2x, а общее решение записывается в виде y = C1ex + C2e2x.
2. Среди корней характеристического уравнения есть кратные. Предположим, что r1 имеет кратность α, а все остальные различны. Рассмотрим вначале случай r1 = 0. Тогда характеристическое уравнение имеет вид:
an(x)·rn+an-1(x)·rn-1+ ... + an-α(x)·rα=0
так как в противном случае r не являлось бы корнем кратности α. Следовательно, дифференциальное уравнение имеет вид:
an(x)·y(n)+an-1(x)·y(n-1)+ ... + an-α(x)·yα=0
то есть не содержит производных порядка ниже α. Этому уравнению удовлетворяют все функции, у которых производные порядка α и выше равны нулю. В частности, таковыми являются все полиномы степени не выше α-1, например,
1, x, x2, …, x α-1. (9)
Покажем, что данная система линейно независима. Составив определитель Вронского этой системы функций, получим
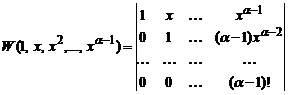.Это определитель треугольного вида с отличными от нуля элементами, стоящими на главной диагонали. Поэтому он отличен от нуля, что и доказывает линейную независимость системы функций (9). Заметим, что в одном из примеров предыдущего параграфа мы доказывали линейную независимость системы функций (9) другим способом. Пусть теперь корнем характеристического уравнения кратности α является число r1≠0. Произведём в уравнении (6) L(y) = 0 замену y = zer1x = z exp(r1x). Тогда
y′=(z′+r1·z)·er1·x, y″=(z″+2r1·z′+r1²·z)·er1·x
и так далее. Подставляя полученные значения производных в исходное уравнение, снова получим линейное однородное уравнение с постоянными коэффициентами
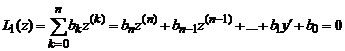(0)
с характеристическим уравнением
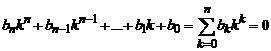. (1)
Отметим, что если k - корень характеристического уравнения (1), то z = ekx- решение уравнения (0), а y = yer1x = e(k+r1)x является решением уравнения (6). Тогда r=k+r1- корень характеристического уравнения (7). С другой стороны, уравнение (6) может быть получено из уравнения (0) обратной заменой z = ye-r1x и поэтому каждому корню характеристического уравнения (7) соответствует корень k = r - r1 характеристического уравнения (1). Таким образом, установлено взаимно однозначное соответствие между корнями характеристических уравнений (7) и (1), причём различным корням одного уравнения соответствуют различные корни другого. Так как r = r1- корень кратности α уравнения (7), то уравнение (1) имеет k=0 корнем кратности α. По доказанному ранее, уравнение (0) имеет α линейно независимых решений
z1=1, z2=x, z3=x², ..., zα=xα-1
которым соответствует α линейно независимых решений
y1=er1·x, y2=x·er1·x, y3=x²·er1·x, ... , yα=xα-1·er1·x, (2)
уравнения (7). Присоединяя полученную систему решений (2) к n- α решениям, соответствующим остальным корням характеристического уравнения, получим фундаментальную систему решений для линейного однородного дифференциального уравнения с постоянными коэффициентами в случае наличия кратных корней.
Пример №2. Для уравнения y'''-4y''+4y' = 0 характеристическое уравнение r3 -4r2 + 4r = 0 имеет корни r=0 кратности 1 и r=2 кратности 2, так как r3 -4r2 + 4r = r(r-2)2, поэтому фундаментальной системой решений исходного уравнения является система функций y1 = 1, y2 = e2x, y3 = xe2x, а общее решение имеет вид y = C1 + C2e2x + C3xe2x .
3. Среди корней характеристического уравнения есть комплексные корни. Можно рассматривать комплексные решения, но для уравнений с действительными коэффициентами это не очень удобно. Найдём действительные решения, соответствующие комплексным корням. Так как мы рассматриваем уравнение с действительными коэффициентами, то для каждого комплексного корня rj = a+bi кратности α характеристического уравнения комплексно сопряжённое ему число rk = a-bi также является корнем кратности α этого уравнения. Соответствующими этим корням парами решений являются функции yjl=xl·e(a+b·i)x и ykl=xl·e(a-b·i)x, l=0,1,.., α-1. Вместо этих решений рассмотрим их линейные комбинации
,l=0,1,.., α-1, которые также являются решениями уравнения L(y)=0 Так как преобразование, осуществляющее переход от yjl, ykl к
, l=0,1,.., α-1, невырожденное, то замена одних совокупностей решений на другие не влияет на линейную независимость получаемой при этом системы решений.
Примеры
1. Для уравнения y''-2y'+5y = 0 корни характеристического уравнения r2 - 2r + 5=0 равны
и фундаментальная система решений состоит из функций y1 = excos2x, y2 = exsin2x а общее решение имеет вид y = C1 excos2x + C2exsin2x.
2. Для уравнения y'''-4y''+13y' = 0 корни характеристического уравнения r3-4r2+13r=0 равны r1=0,
и фундаментальная система решений состоит из функций y1 = 0, y2 = e2xcos3x, y3 = e2xsin3x , а общее решение имеет вид y = C1 + C2e2xcos3x + C3e2xsin3x.
3. Для уравнения y(4) + 8y'' + 16y =0 характеристическое уравнение r4+8r2+16=0 имеет r1 = 2i, r2 = -2i кратности 2, так как r4+8r2+16= (r2 + 4)2, поэтому фундаментальной системой решений исходного уравнения является система функций y1 = cos2x, y2 = sin2x, y3 = xcos2x, y4 = xsin2x, а общее решение имеет вид y = C1cos2x+ C2sin2x+ C3xcos2x+ C4xsin2x.